Презентація "Розміщення, перестановка та комбінація"
Про матеріал
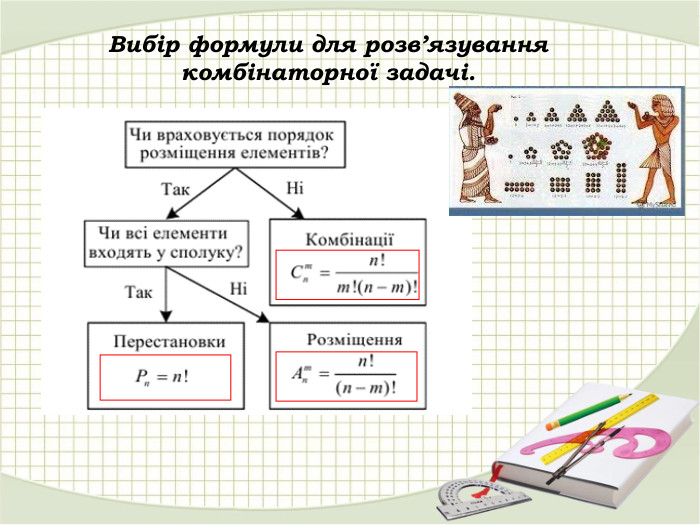
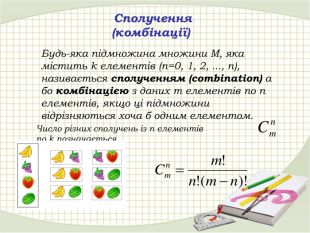
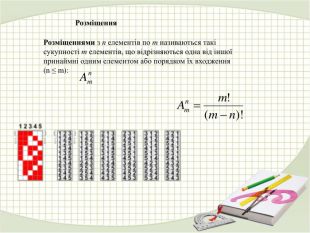
Матеріал презентації "Розміщення, перестановка та комбінація" можна використати на уроках алгебри 11 класу. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку