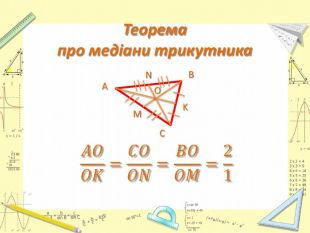
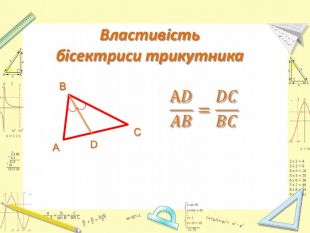
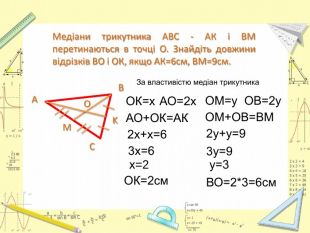
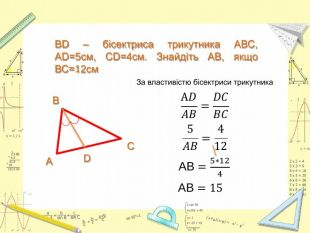
Презентація "Розв’язання задач за темами: Узагальнена теорема Фалеса. Теорема про медіани трикутника. Властивість бісектриси трикутника."
Про матеріал
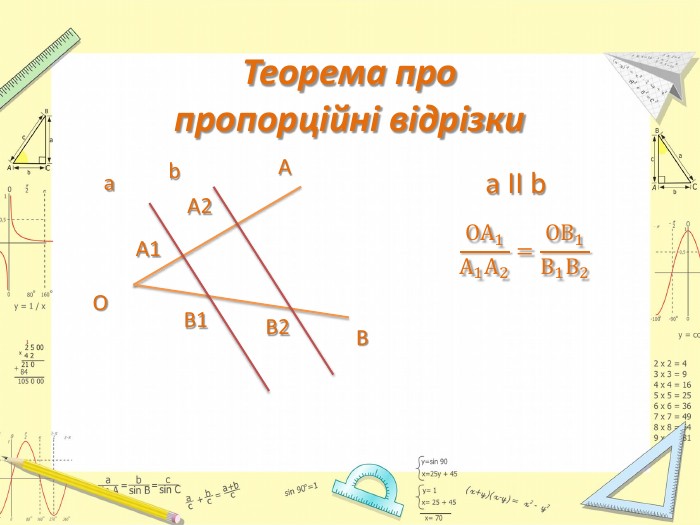
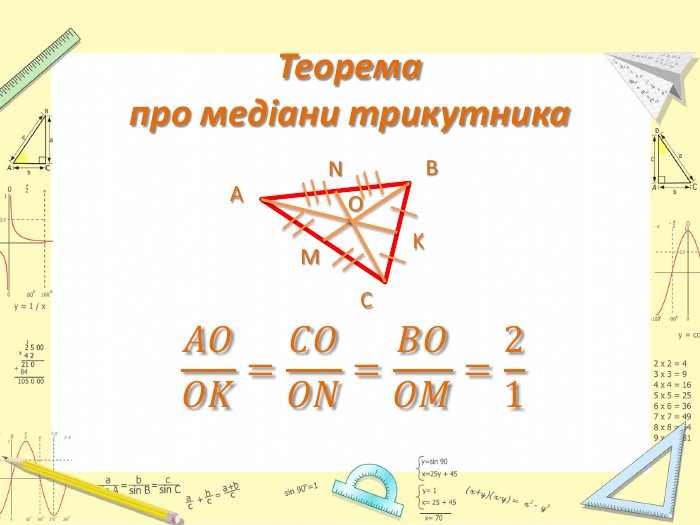
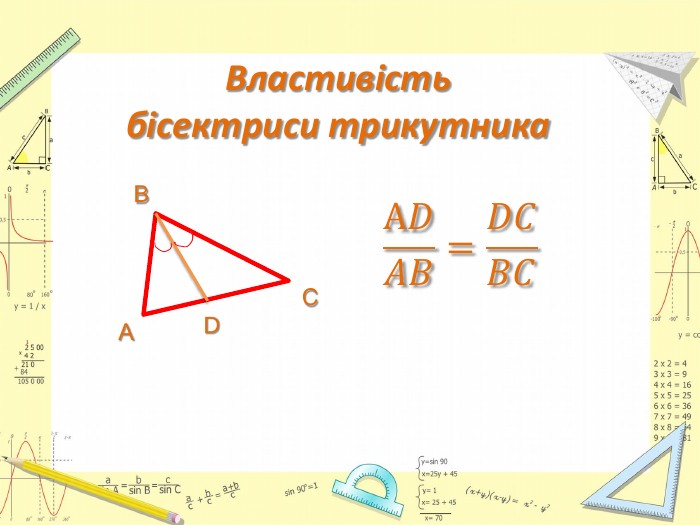
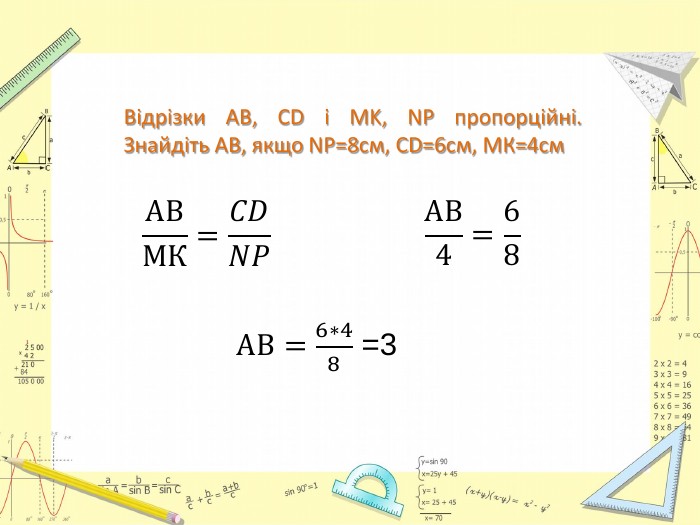
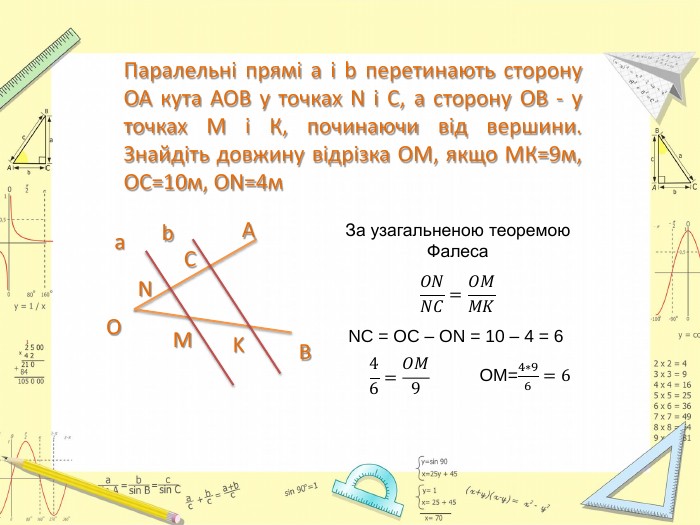
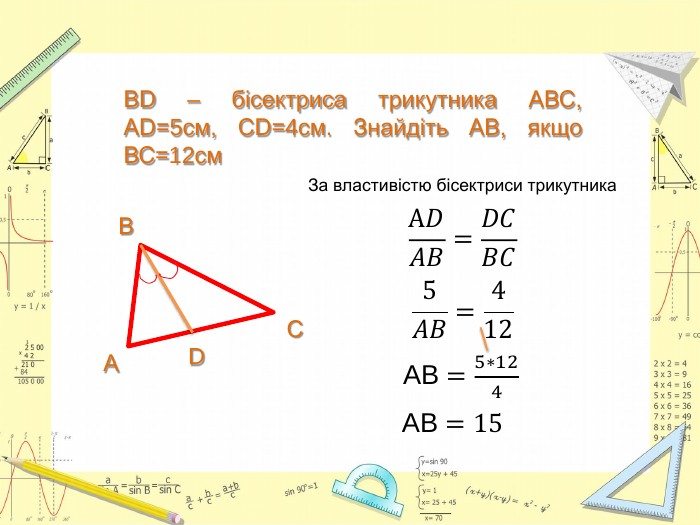
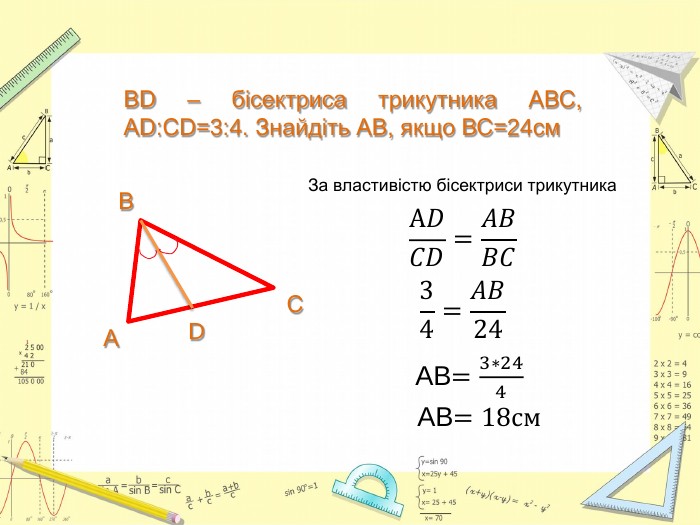
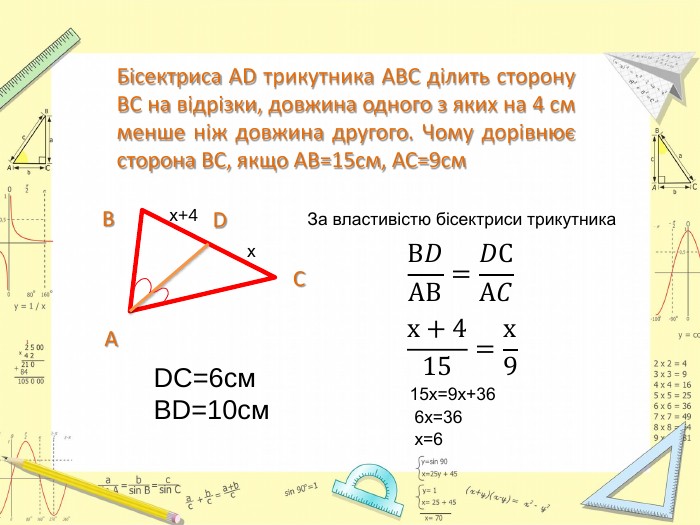
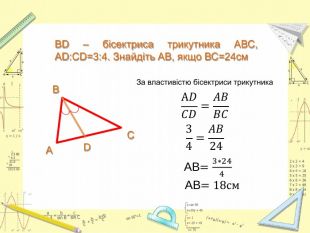
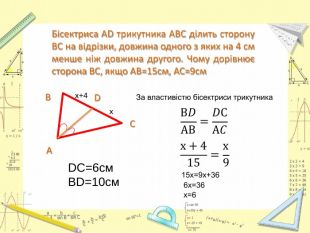
Презентація до уроку Геометрії у 8 класі. Повторення узагальненної теореми Фалеса, теореми про медіани трикутника, властивості бісектриси трикутника. Розв'язання задач, підготовка до тестування. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







-

Воронцова Світлана Петрівна
19.02.2025 в 09:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Скутельник Ганна Олександрівна
27.01.2025 в 19:29
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сирота Любов Іванівна
17.12.2024 в 06:39
Дякую за чудовий матеріал.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Данилець Вікторія
04.12.2023 в 18:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук