Презентація "Розв’язування компетентнісно орієнтованих задач"
Про матеріал
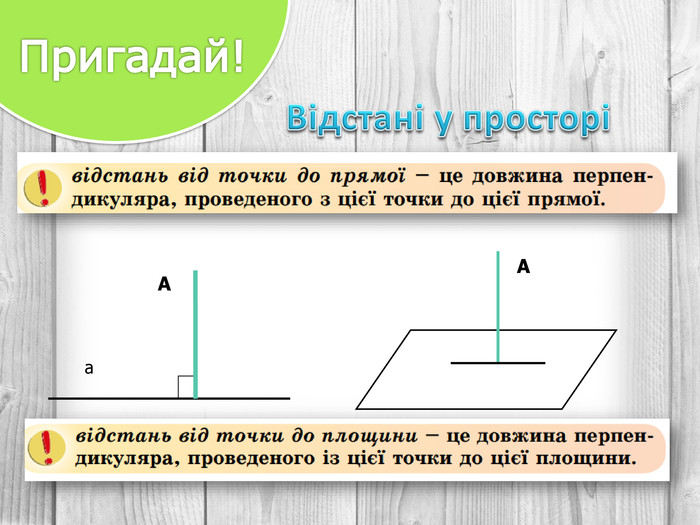
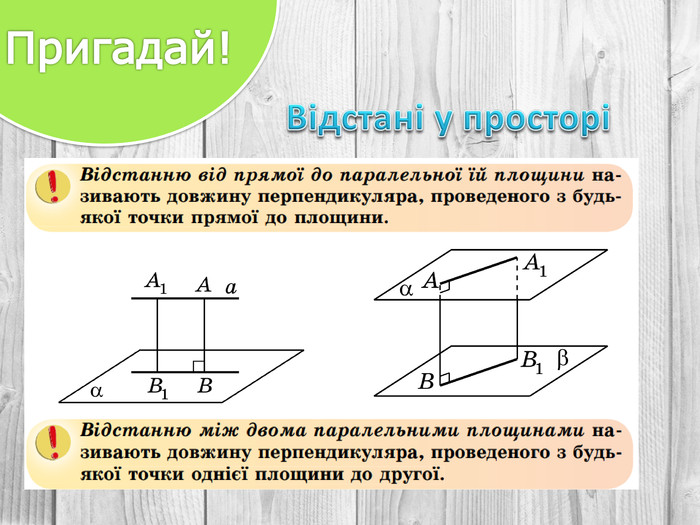
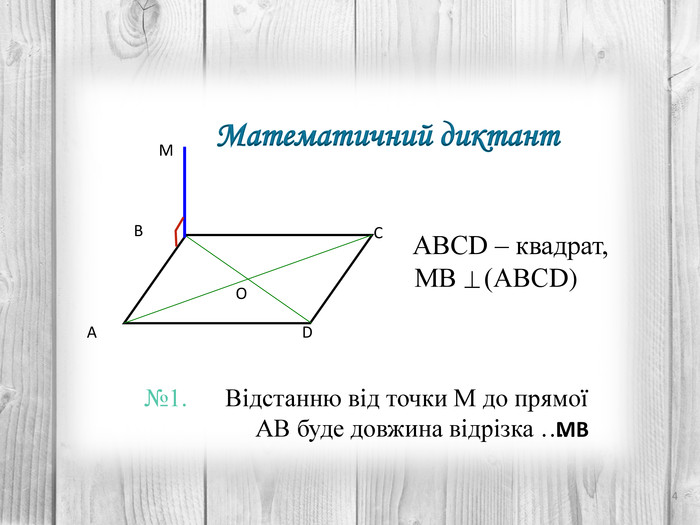
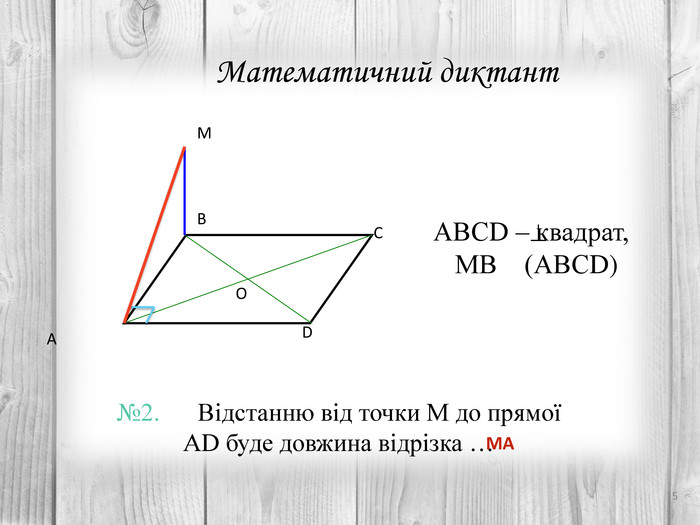
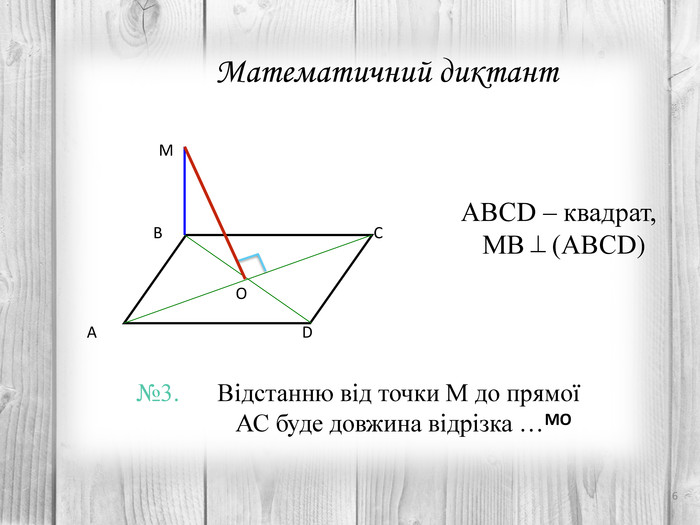
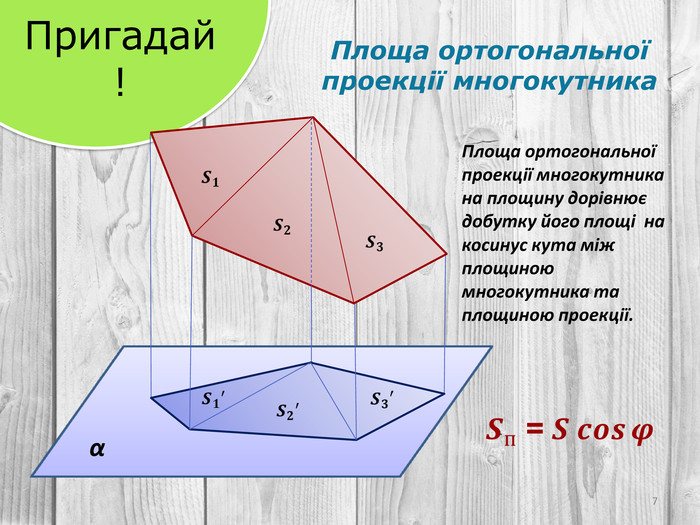
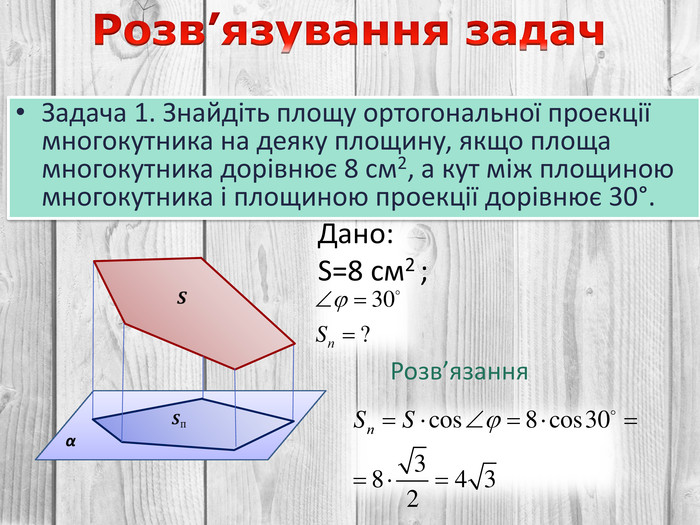
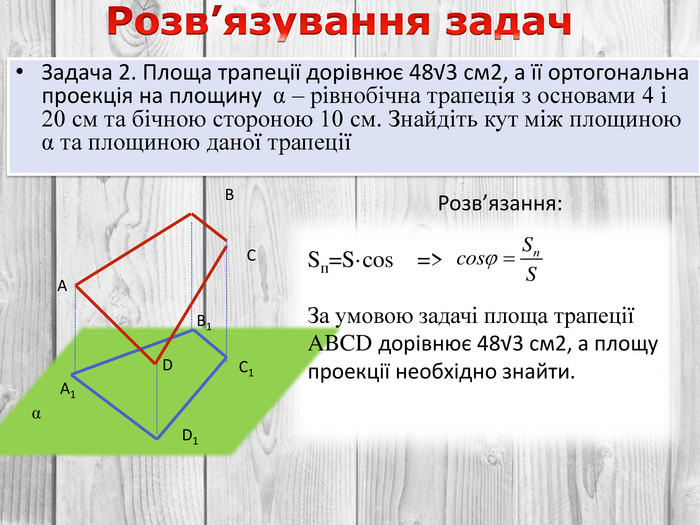
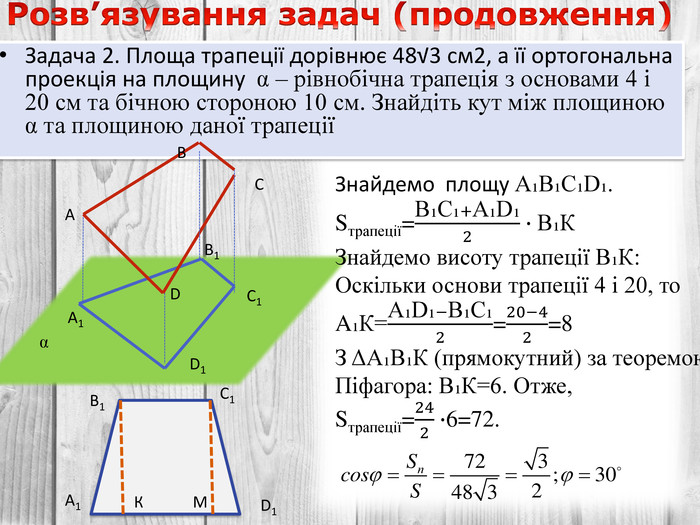
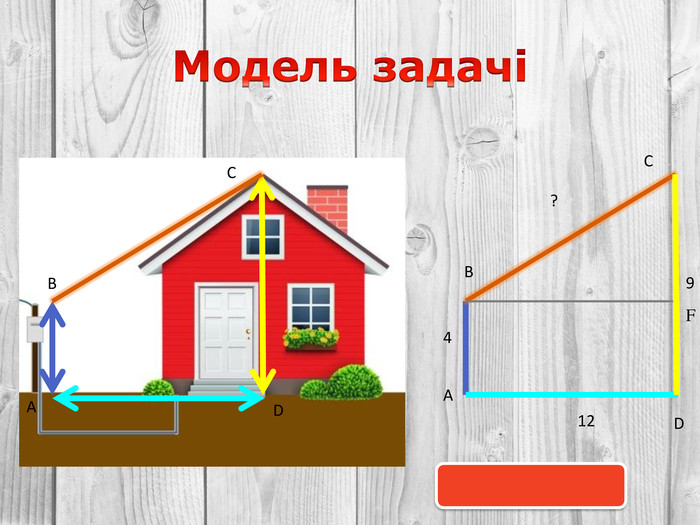
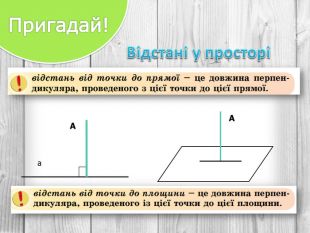
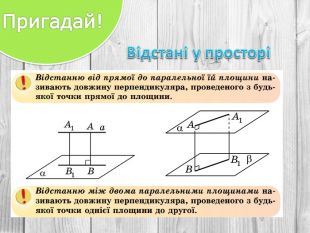
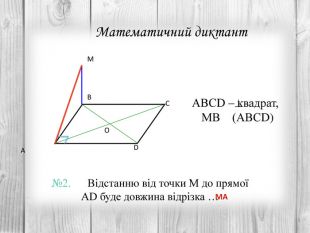
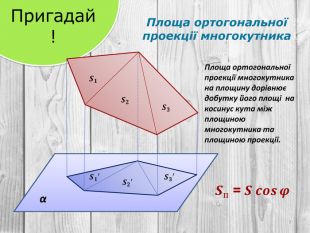
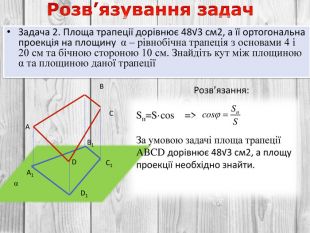
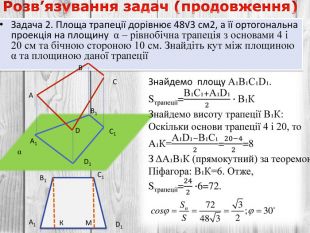
Розв’язування компетентнісно орієнтованих задач до теми "Перпендикулярність прямих і площин у просторі" за підручником Математика 10 клас (рівень стандарт) ав. Істер О.С. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку