Презентація,, Розв'язування лінійних нерівностей із знаком модуля"
Про матеріал
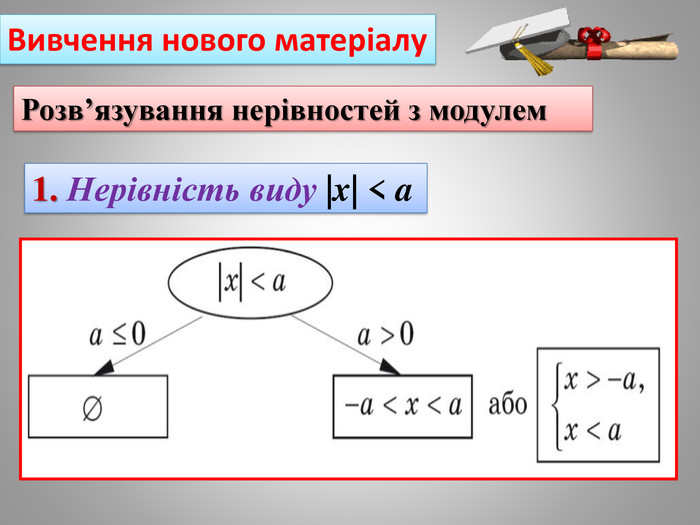
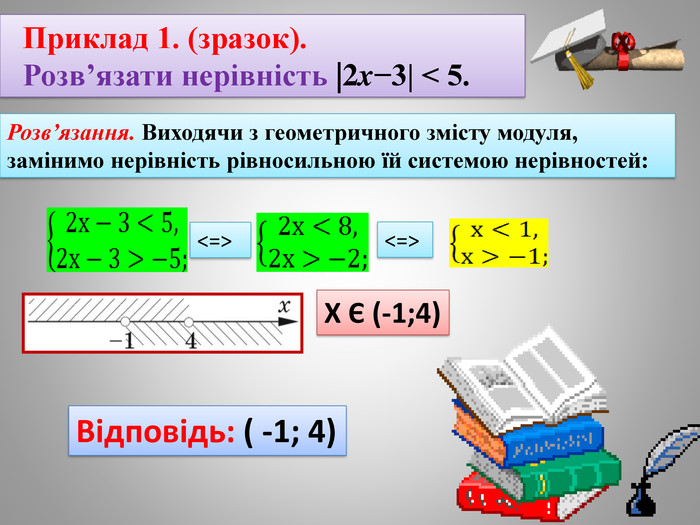
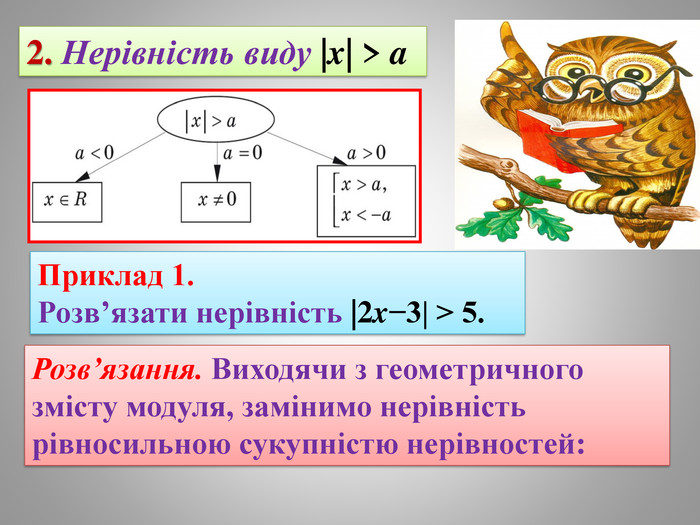
В даній презентації пригадано визначення модуля,показано як використовувати його означення можна навчитися розв'язувати лінійні нерівності з однією змінною.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Істер О. С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку









![Виконання письмових вправ1. Знайдiть на координатнiй прямiй множину чисел, якi задовольняють нерiвнiсть, i запишiть цю множину у виглядi промiжку або об’єднання промiжкiв:1)|x| < 3; 2) |x| > 4; 3) |x+1| > 10,5; 4) |x−3| ≤ 4,7. Відповіді:1) (-3; 3);3) (-∞; -11,5); (9,5;+∞);4) [-7,7; 1,7];2) (-∞; -4); (4;+∞); Виконання письмових вправ1. Знайдiть на координатнiй прямiй множину чисел, якi задовольняють нерiвнiсть, i запишiть цю множину у виглядi промiжку або об’єднання промiжкiв:1)|x| < 3; 2) |x| > 4; 3) |x+1| > 10,5; 4) |x−3| ≤ 4,7. Відповіді:1) (-3; 3);3) (-∞; -11,5); (9,5;+∞);4) [-7,7; 1,7];2) (-∞; -4); (4;+∞);](/uploads/files/29885/43994/46057_images/12.jpg)
![2. Розв’яжiть нерiвнiсть:1) (x−1)(2x+5) > 0; Відповідь:1) (1; +∞), або ( -∞; -2,5);Відповідь:2) [ 0,5; 2] 2. Розв’яжiть нерiвнiсть:1) (x−1)(2x+5) > 0; Відповідь:1) (1; +∞), або ( -∞; -2,5);Відповідь:2) [ 0,5; 2]](/uploads/files/29885/43994/46057_images/13.jpg)