Урок «Перші відомості про математичну статистику. Вибірка, гістограма, середнє значення, мода і медіана вибірки».

Тема: «Перші відомості про математичну статистику. Вибірка, гістограма, середнє значення, мода і медіана вибірки».

Мета: Ознайомити учнів з історією виникнення математичної статистики, її методами дослідження, розвивати уміння аналізувати, робити висновки, прищеплювати математичну культуру, показати застосування набутих знань у практичній діяльності.

Хід уроку

І. Організаційний момент.

ІІ. Історична довідка.

Термін «статистика» походить від латинського слова status – стан, становище. Статистика – наука, що збирає, обробляє, вивчає різні дані, пов’язані з масовими явищами, процесами і подіями. Предметом вивчення статистики є кількісна сторона масових суспільних явищ і процесів у зв’язку з їхньою якісною стороною.

Математична статистика – розділ прикладної математики, присвячений методам систематизації, обробки й використання статистичних даних для наукових і практичних висновків.

Статистика виникла з практичних потреб людей, їх господарської діяльності, необхідності обліку земельних угідь, майна, кількості населення, його зайнятості, вікового складу. У XVII ст.. в Англії зародилася наука «політична арифметика», засновниками якої були англійські вчені               Дж. Граунт та І. Петті . вони не лише описували факти, а й аналізували цифрові дані про явища суспільного життя, виявляли притаманні їм закономірності.

Значних результатів у статистиці досягли видатні українські математики В. Я. Буняковський та М. П. Кравчук.

ІІІ. Вивчення нового матеріалу.

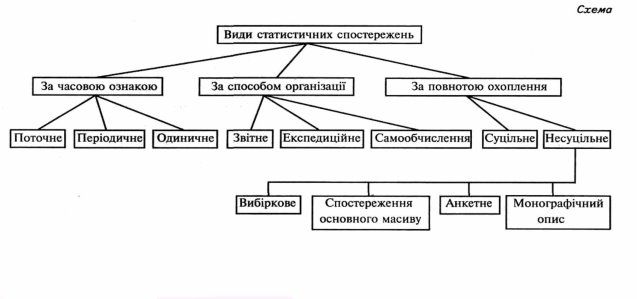
У процесі статистичних досліджень застосовують особливі прийоми вивчення, які в сукупності утворюють статистичний метод. На схемі систематизовано види статистичних спостережень.

Найпростішим видом несу цільного спостереження  є вибіркове спостереження. Сукупність одиниць, відібраних для вибіркового спостереження, називають вибіркою. Статистичне дослідження проводять у три етапи:

1. визначають мету дослідження і об’єкти, які будуть досліджуватися;
2. використовують різні методи збирання даних;
3.   результати статистичних досліджень обробляють і оформляють у вигляді таблиць, діаграм, графіків.

IV. Розв’язування вправ.

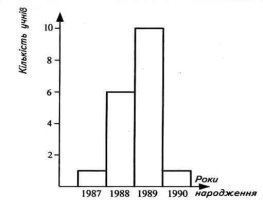
Приклад 1. В одному з класів школи були учні різних років народження. З’ясувалося, що 1987 р. і 1990 р. було по одному учню, 1988 р. народження – 6 учнів і 10 учнів 1989 р. народження.

Розв’язання

Ці дані можна подати таблицею:

А можна побудувати стовпчасту діаграму ( у статистиці їх називають гістограмами).

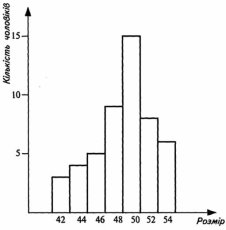
Приклад 2. Швейній майстерні потрібно з’ясувати, скільки чоловічих пальт і яких розмірів пошити. Опитавши 50 чоловік, їх розміри записали в таблицю:

Це – вибірка з 50 значень (даних). Для зручності її групують у класи (за розмірами) і підраховують, скільки значень вибірки містить кожний клас.

Такі таблиці називаються частотними. В них числа другого рядка – частоти; вони показують, як часто зустрічаються у вибірці ті чи інші її значення. Відносною частотою значення вибірки називають відношення його частоти до числа всіх значень вибірки. У розглянутому прикладі частота розміру 44 дорівнює 4, а відносна частота – 8%.

За частотною таблицею можна побудувати гістограму.

Вибірки характеризують центральними тенденціями: середнім значенням, модою та медіаною. Середнім значенням вибірки називають середнє арифметичне усіх її значень. Мода вибірки – те її значення, яке трапляється найчастіше. Медіана вибірки – це число, яке «поділяє» навпіл упорядковану сукупність усіх значень вибірки.

Приклад 3. У вибірці з 9 учнів отримали такі дані про їх зріст: 170см, 176см, 165см, 167см, 179см, 185см, 175см, 180см, 177см. Знайти центральні тенденції вибірки.

Розв’язання

Упорядкуємо дану вибірку: 165, 167, 170, 175, 176, 177, 179, 180, 185.

Знайдемо середнє арифметичне вибірки.

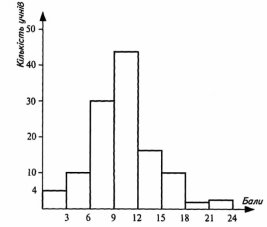
Приклад 4. За розв’язання задач п’ять учасників олімпіади одержали від 0 до 3 балів, десять – від 4 до 6, тридцять – від 7 до 9, сорок чотири – від 10 до 12, шістнадцять – від 13 до 15, десять – від 16 до 18, два – від 19 до 21, три  від 22 до 24 балів. Складіть частотну таблицю, побудуйте гістограму.

1. Складаємо частотну таблицю:

2. Побудуємо гістограму.

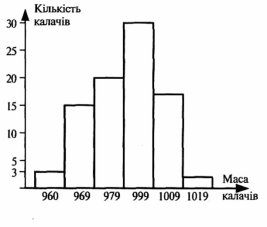
Приклад 5. Пекарня випікає кілограмові калачі. Під час перевірки виявилося, що маса трьох калачів менша від 1кг на 31-40г, п’ятнадцяти – на 21-30г, двадцяти – на 11-20г, тридцяти – на 1-10г; маса сімнадцяти калачів більша від 1кг на 0-9г, а двох – на 10-19г. Побудуйте відповідну гістограму.

Будуємо гістограму.

V. Підсумок уроку.

VI. Домашнє завдання. [5, c.9]