УРОК-ПРЕЗЕНТАЦІЯ "МЕТОД МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ"

УРОК-ПРЕЗЕНТАЦІЯ МЕТОДУ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ (Урок алгебри в 9 класі)

Тема: Математичне моделювання

Мета: сформувати поняття математичного моделювання, розглянути загальне завдання математичного моделювання, показати застосування методу математичного моделювання в різних галузях життя, розвивати культуру мислення, виховувати пізнавальний інтерес.

Обладнання: плакат з висловом: „Використання математичних моделей у різних науках, багатьох галузях людської діяльності показало велике значення цього методу для успішного розвитку останніх” (А. М. Тихонов).

ХІД РОКУ

Вступне слово вчителя

Сьогодні на уроці ви ознайомитеся з новими поняттями — методом математичного моделювання та математичними моделями. Їх будуть презентувати вчений-математик, інженер-конструктор, лікар, еколог, економіст та інші (називає прізвища учнів, які будуть вести урок). Тож надаємо їм слово.

Математик-соціолог. Слово „модель” у повсякденному житті ви чули неодноразово. Так, у газетах можна прочитати, наприклад, що запропонована модель гри футбол певної команди виявилася результативною або, навпаки, не виправдала себе. Моделі можна зустріти в хореографії, віршуванні, економіці, інженерії, архітектурі. Моделі літаків, машин, кораблів супроводжують дитинство кожного хлопчика, а моделі одягу мають особливе значення в житті дівчаток.

Зазвичай в різних ситуаціях замість слова модель говорять: «схема», «креслення», «проект» тощо. Однак усі ці поняття мають приблизно ,один і три самий зміст. Він полягає в тому, що якесь складне реальне явище ми замінюємо деякою спрощеною схемою, копією. Так, інженер вивчає і передбачає роботу верстата за кресленнями — моделями верстата. Хореограф конструює танець не на сцені, а на папері, де партнери зображаються квадратиками, а партнерші — кружечками. Це схема-модель майбутнього танцю. Композитор, створивши мелодію, записує її за допомогою нот. Ноти мелодії — це її модель. Особливого значення набуває моделювання в техніці.

Моделюванням називають побудову копії (моделі) якогось явища, процесу, об'єкта тощо.

Інженер-конструктор. Я хочу сказати, що в науці і практиці добре відомий метод фізичного моделювання. Ним користуються в різних галузях машинобудування, приладобудування, будівельній справі. Адже, перш ніж створити нову машину, літак, корабель чи верстат, інженер-конструктор створює зменшену модель об'єкта, досліджує необхідні параметри його діяльності, вдосконалює, а потім виробляється власне об'єкт — машина, літак та ін. Процеси, які відбуваються в моделі й оригіналі, мають однаковий характер.

Необхідність створення фізичних моделей диктується багатьма практичними завданнями. Наприклад, Волховську ГЕС будували на такому місці, де залягав пісок. За. правилами гідротехніки, його потрібно було виймати і греблю будувати на гранітній основі. Все це, звичайно, вимагало багато коштів, матеріалів, часу. Під керівництвом відомого інженера Графтіо була створена модель русла річки, за якою дослідили, як змінюватиме положення гребля під тиском води, якщо вона побудована на піщаній основі. Зроблені висновки мали велике практичне значення. ГЕС було побудовано з найменшими витратами.

Учений - математик. Особливу роль у науці та практиці відіграють математичні моделі. Що ж таке математична модель?

Розглянемо задачу. Поживність 1 кг сіна складає 0,42, а силосу — 0,20 кормових одиниць. Сіно містить 85 %, а силос — 27 % сухої речовини. Скільки сіна і скільки силосу потрібно давати корові на добу, якщо вона повинна отримати 6 кормових одиниць і 9 кг сухої речовини?

Розв'язання. Нехай раціон корови містить х кг сіна і у кг силосу. Тоді маємо:

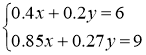
кг, кг.

У цій задачі ми мали справу з нематематичними поняттями: сіно, силос, корова, кормові одиниці. Це прикладна задача. Щоб її розв'язати, складаємо систему рівнянь, що є математичною моделлю даної прикладної задачі.

Моделлю називають спеціально створений об'єкт, який відображає властивості досліджуваного об'єкта.

Математичні моделі створюють із математичних понять і відношень: геометричних фігур, чисел, функцій, рівнянь, нерівностей, їх систем. Розв'язування прикладної здачі здійснюється в три етапи:

1. Створення математичної моделі пропонованої задачі (для нашого прикладу — це система двох лінійних рівнянь з двома невідомими).

2. Розв'язування відповідної математичної задачі.

3. Аналіз відповіді.

Схематично ці етапи можна показати так:

Тут А — прикладна задача, В — її математична модель, С — відповідь для моделі, D — відповідь до прикладної задачі. Аналіз відповіді є важливим етапом розв'язання задачі. Адже буває так, що корінь рівняння, що є моделлю задачі, задовольняє рівняння, але не задовольняє умову задачі.

Перехід від А до В — це створення потрібної моделі, тобто процес моделювання. Взагалі, щоб створити модель, треба знати не лише математику, а й ту прикладну галузь, про яку йдеться у задачі. Запам'ятайте, що математичними моделями здебільшого є функції, рівняння, нерівності, системи рівнянь та системи нерівностей.

Наприклад, система рівнянь

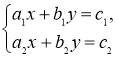
є математичною моделлю напруги в електричному колі (в електротехніці), рівноваги для системи важелів або пружин (у механіці), завантаженості верстатів (у плануванні) та ін.

Функція є математичною моделлю, яка описує зростання продуктивності праці, зміну атмосферного тиску розмноження бактерій, приріст деревини, населення, збільшення вантажопідйомності транспорту тощо.

Лікар. Математичному моделюванню відведено значну роль і в медицині. За допомогою математичного моделей можна створити органи людини. Що ж собою являє така модель? У найпростішому випадку – це формули, частіше – системи з десятків і сотень рівнянь, нерівностей, які математично виражають діяльність окремих органів людини, перебіг біологічних процесів в організмі.

Саме з математичним моделюванням, на думку вчених зв’язний процес визволення людства від багатьох недугів, у тому числі й серцево-судинних захворювань.

А чи можна, не чекаючи спалаху грипу чи іншого інфекційної захворювання, передбачити, ти почнеться епідемія? Тік. Учені-медики уже створили математичну модель грипу. Це формули з кількома десяткам інтегралів і систем рівнянь; нерівностей. За їх допомогою визначають, чи хвора людина стає особливо безпечною, яка кількість жителів регіону буде охоплена хворобою і в який період. Такий діагноз дозволяє медикам завчасно підготувати профілактичні та лікувальні засоби.

В Інституті серцево-судинних захворювань створено лабораторію математичного моделювання. Тепер стало можливим створювати індивідуальні математичні моделі відповідно до стану здоров'я кожного пацієнта і за їх допомогою лікувати небезпечні хвороби.

Вчений еколог. Математичні моделі знаходять широке застосування в екології. Так, у Науково-дослідному інституті водних проблем розроблені математичні моделі прогнозування якості води в Чорному та Азовському морях. Створені моделі дозволяють передбачити негативні зміни, які загрожують екосистемі цих водних басейнів, та вжити своєчасно заходів, що запобігають забрудненню та руйнівній експлуатації їх багатств.

Математики й біологи побудували математичні моделі співіснування видів, один з яких є хижаком відносно іншого. Ця модель є системою двох диференціальних рівнянь. Дослідження цієї моделі показало, що хижак повністю знищує інший вид. Види співіснують, періодично замінюючи свою чисельність. Тому не можна винищувати, наприклад, вовків. Все в природі має право на життя.

Економіст. Математичні моделі набули широкого застосування в економіці. Розглянемо задачу. Треба скласти математичну модель заробітної платні робітникам згідно з відрядно-преміальною системою.

Нехай z – заробітна платня, х – кількість виготовленої продукції, а – тарифна ставка одиниці продукції, р – премія за перевиконування норми.

Маємо модель:

Економіко-математичні моделі дозволяють розв’язувати багато задач, зокрема так званих оптимізацій них, які виникають у найрізноманітніших видах людської діяльності. Ось одна з таких задач.

У цеху одного із заводів випускають прилади двох видів. Виробнича потужність цеху - 100 приладів першого виду або 300 другого виду. Але відділ технічного контролю в змозі перевірити тільки 150 виробів на добу. Крім того, вироби першого виду вдвічі дорожчі за вироби другого виду. Потрібно скласти такий план випуску продукції, який за даних умов забезпечував би цеху найбільший прибуток. (Ми її розв'яжемо на занятті гуртка.)

Учений-кібернетик. Останнім часом у життєвій практиці використовується імітаційне моделювання. Що ж таке імітаційна модель? Це математична модель з подальшим дослідженням та експериментами на ЕОМ. Імітаційне моделювання застосовується у випадках, коли прямий експеримент неможливий. Так, у лабораторії не можна змоделювати атмосферні процеси, зробити термоядерний реактор або штучно відтворити етапи розвитку Всесвіту. Тут на допомогу приходить імітаційне моделювання. Тож математиками, фізиками й біологами були розроблені моделі глобальних біосферних процесів, які можуть відбутися після ядерної війни. Результати імітаційного моделювання показали, що ядерний конфлікт призведе не тільки до загибелі людей від радіації, вибухів, генетичних змін. У результаті ядерних вибухів на всій планеті розпочнуться самопідтримуючі пожежі. В атмосфері будуть носитися величезні хмари сажі, пилу. Настане так звана ядерна ніч. На Землі запанує ядерна зима. Температура знизиться до - 40°-50°. Все живе на Землі зникне.

Тож завдання народів світу — зберегти мир на планеті.

Вчитель. А тепер перевіримо, як ви зрозуміли прослуханий матеріал. Прошу дати відповіді на запитання:

1. Де ви зустрічали моделі в повсякденному житті?

2. Що таке фізичні моделі (моделювання)? Де вони зустрічаються?

3. Що таке математична модель?

4. Де використовується метод математичного моделювання?

5. Що таке імітаційне моделювання? Де воно використовується?

Домашнє завдання.

№ 277, № 278, № 285, § 63.

Підсумок уроку.