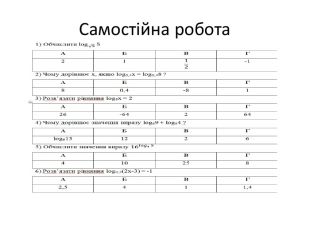
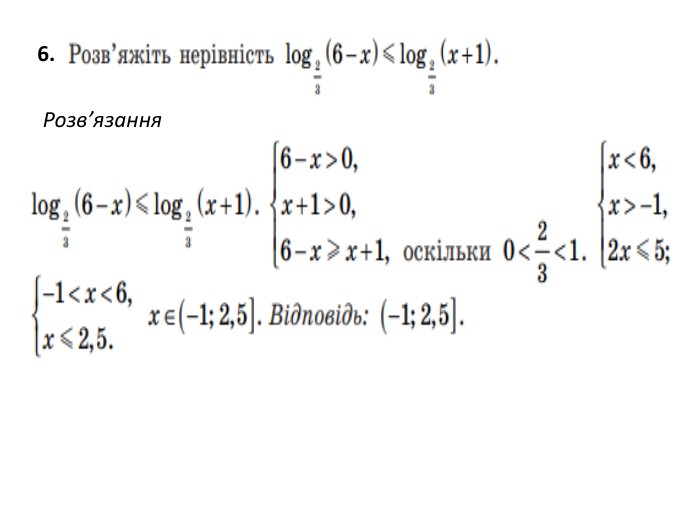Презентація. "Розв'язування логарифмічних рівнянь і нерівностей."
Про матеріал
Узагальнити і систематизувати знання з теми "Логарифмічна функція."
Розвивати навички розв'язування логарифмічних рівнянь і нерівностей.
Перевірити рівень засвоєння даної теми. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку