презентація "Розв’язування задач з теми: Рух тіла під дією кількох сил по горизонталі""
Про матеріал
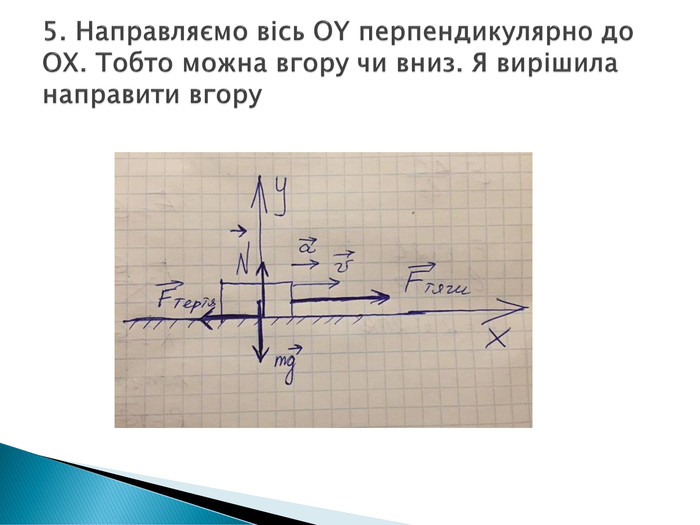
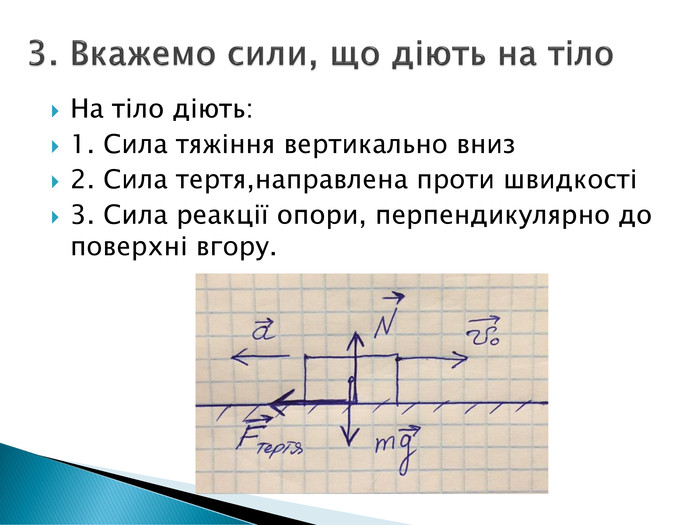
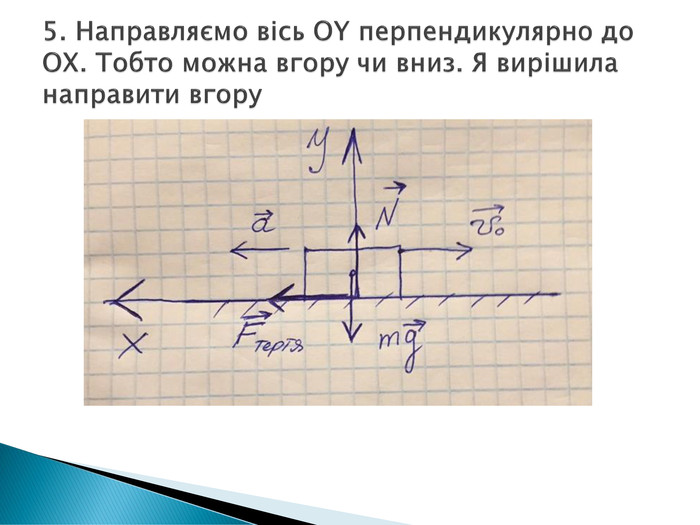
презентація "Розв’язування задач з теми: Рух тіла під дією кількох сил по горизонталі"" з прикладами розв"язання задач і задачами для самостійного опрацювання Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Фізика 9 клас (Бар'яхтар В.Г., Довгий С.О., Божинова Ф.Я., Кирюхіна О.О. (за редакцією Баряхтара В.Г., Довгого С.О.))
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку