Презентація «Розвиток пізнавальної активності учнів у процесі вивчення математики».

Проблема «Розвиток пізнавальної активності учнів у процесі вивчення математики».

Завдання спрямовані на формування і розвиток в учнів: цілісного сприйняття світу, розуміння ролі математики у пізнанні дійсності; готовності до розпізнавання проблем, які можна розв’язати математичними методами, здатності розв’язувати контекстні задачі; здатності логічно міркувати, обґрунтовувати свої дії, виконувати дії за алгоритмом; готовності застосовувати обчислювальні навички у практичних ситуаціях; уміння користуватися математичною термінологією, знаковою і графічною інформацією; здатності орієнтуватися на площині та в просторі; розуміння сутності процесу вимірювання величин; » інтересу до вивчення математики; творчого підходу та емоційно-ціннісного ставлення до виконання математичних завдань; уміння навчатися.

Математичні поняття молодших школярів ефективно формуються за допомогою пізнавальних завдань,спрямованих на розвиток мислительного компонента навчальної діяльності. Пізнавальні завдання сприяють формуванню поняття про конкретні об’єкти, явища навколишнього світу і потребують певних розумових зусиль. Такі завдання передбачають активний пошук, де вчаться розрізняти істотні і неістотні ознаки, виділяють головне, міркують, а не сприймають готову відповідь чи відтворюють добре засвоєні дії. Для стимулювання пізнавальної діяльності учнів корисно:- доповнювати математичний зміст завдань різними практичними проблемами;- з’ясовувати зв’язки виучуваного з життям;- подавати матеріал у цікавій формі;- творчо опрацьовувати одержану інформацію. Треба правильно спрямовувати ігрову діяльність учнів, підготувавши необхідні наочні посібники, демонстраційний матеріал, відео-матеріали, широко використовувати ІКТ, інтернет-ресурси

Задачі в математичній освіті посідають особливе місце. Це специфічний розділ програми, зміст якого учні мають засвоїти, а з другого – виступають як дидактичний засіб навчання і розвитку школярів. Функції задач1. пізнавальна (з’ясування елементів арифметичної теорії)2. дидактична (загальне складне уміння розв’язувати задачу)3. розвивальна (логічне мислення, аналіз, синтез, порівняння, узагальнення)4. виховна (формує моральні риси особистості, активна громадянська позиція). Діяльність учнів над розв’язанням задачі на уроці організовується у формі:- колективної фронтальної роботи; - індивідуальної самостійної роботи;- напівсамостійної групової роботи.

На розвиток пізнавальних інтересів учнів позитивно впливають такі види завдань з логічним навантаженням:- завдання з елементами дослідження ( вправи зі словами: «порівняйте», «відмітьте головне», «обґрунтуйте», «доведіть», «узагальніть» та інше);- завдання, при виконанні яких учні «відкривають» для себе зв’язки, залежності, закономірності тощо і переконуються в їх справедливості (вправи на здійснення простих висновків, класифікацій та групування предметів);- практичні вправи і завдання на використання різних тверджень. Глибше усвідомити зв’язки і залежності між величинами в задачах допомагають спеціальні вправи функціонального змісту. Їх три групи: - задачі-запитання;- прості задачі підвищеної трудності;- приклади, що пропонуються парами. Вправи функціонального змісту розвивають логічне мислення дітей, їхню кмітливість, комбінаторні здібності, а головне – сприяють усвідомленню математичних закономірностей, формуванню навичок свідомого вибору дій, практичних умінь і загалом підвищують культуру мислення.

Характер навчально-пізнавальної діяльності учнів відображають такі структурні елементи: - постановка й усвідомлення учнями пізнавального завдання; - сприймання навчального матеріалу; - осмислення навчального матеріалу і засвоєння його основної інформації; - формування наукових понять, узагальнення і систематизація; - закріплення і удосконалення знань, їх запам’ятовування, формування навичок і вмінь; - застосування навичок у практиці, використання у життєвих ситуаціях; - зворотній зв’язок і перевірка засвоєння, аналіз і самоаналіз досягнень учнів. Відтворення і закріплення набутих знань. Розвиток самостійності творчостіПізнавальні завдання поділяються на:

У роботі з нестандартними завданнями домінує пізнавальна гра. Дуже корисні завдання: на розвиток і удосконалення уваги; на розвиток сприйняття і уяви; на розвиток пам’яті; на розвиток мислення. Математичні завдання умовно можна поділити на: Виділяють такі групи вправ: завдання, пов’язані з важливими поняттями і методами математики; вправи з елементами дослідження; практичні завдання і вправи; самостійно складені учнями вправи спочатку за аналогією, пізніше за даною умовою; вправи на кмітливість; вправи з логічним навантаженням, математичні ребуси, кросворди; цікаві вправи та ігри. Стандартні (розв’язання за відомим алгоритмом,зразком, аналогією)Нестандартні (творчі)

Розрізняють кілька рівнів у системі пізнавальних завдань і творчих тренувальних вправ за їх складністю. Завдання першого рівня стверджувальні (учень лише обґрунтовує твердження). Завдання другого рівня дають змогу самостійно дійти певних висновків, довести їх правильність тощо. Вправи й задачі третього рівня стимулюють дітей до активної розумової діяльності, до творчого пошуку. Глибше усвідомити зв’язки і залежності між величинами в задачах допомагають спеціальні вправи функціонального змісту. Їх три групи: - задачі-запитання; - прості задачі підвищеної трудності; - приклади, що пропонуються парами. Вправи функціонального змісту розвивають логічне мислення дітей, їхню кмітливість, комбінаторні здібності, а головне – сприяють усвідомленню математичних закономірностей, формуванню навичок свідомого вибору дій, практичних умінь і загалом підвищують культуру мислення.

Найбільший вплив на розвиток математичних здібностей школярів мають такі вправи: 1) логічного змісту; 2) комбінаторні; 3) з елементами дослідження; 4) на кмітливість. Два хлопчики грали на гітарі, а один на баяні. На якому інструменті грав Юрко, якщо Михайлик з Петриком та Петрик з Юрком грали на різних інструментах?У коробці 7 червоних і 5 синіх олівців. Яку найменшу їх кількість треба взяти навмання, об серед них обов’язково було б хоча 2 червоних?Визнач правило, за яким складено ряд чисел, і напиши наступне число: а) 1,2,4,8 …, б) 1, 14, 27, 40 … . У двох хлопчиків є поштові листівки. Коли б перший подарував другому одну листівку, х стало б у 2 рази більше, ніж у першого. А коли б другий подарував першому одну листівку, то листівок стало б порівну. Скільки листівок у кожного хлопчика?

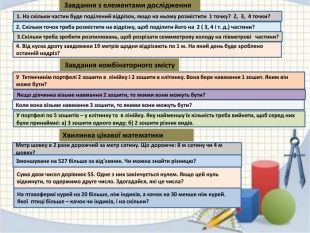
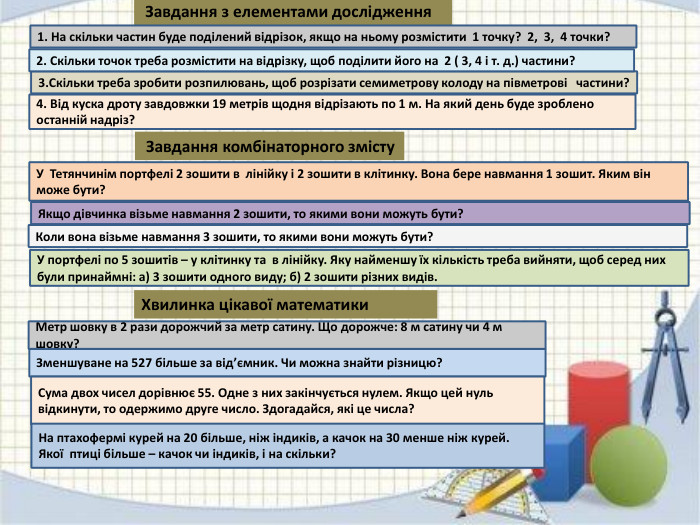
Завдання з елементами дослідження1. На скільки частин буде поділений відрізок, якщо на ньому розмістити 1 точку? 2, 3, 4 точки?4. Від куска дроту завдовжки 19 метрів щодня відрізають по 1 м. На який день буде зроблено останній надріз?3. Скільки треба зробити розпилювань, щоб розрізати семиметрову колоду на півметрові частини?2. Скільки точок треба розмістити на відрізку, щоб поділити його на 2 ( 3, 4 і т. д.) частини? Завдання комбінаторного змісту. У портфелі по 5 зошитів – у клітинку та в лінійку. Яку найменшу їх кількість треба вийняти, щоб серед них були принаймні: а) 3 зошити одного виду; б) 2 зошити різних видів. Якщо дівчинка візьме навмання 2 зошити, то якими вони можуть бути?Коли вона візьме навмання 3 зошити, то якими вони можуть бути?Хвилинка цікавої математики. У Тетянчинім портфелі 2 зошити в лінійку і 2 зошити в клітинку. Вона бере навмання 1 зошит. Яким він може бути?Метр шовку в 2 рази дорожчий за метр сатину. Що дорожче: 8 м сатину чи 4 м шовку?Зменшуване на 527 більше за від’ємник. Чи можна знайти різницю?Сума двох чисел дорівнює 55. Одне з них закінчується нулем. Якщо цей нуль відкинути, то одержимо друге число. Здогадайся, які це числа?На птахофермі курей на 20 більше, ніж індиків, а качок на 30 менше ніж курей. Якої птиці більше – качок чи індиків, і на скільки?

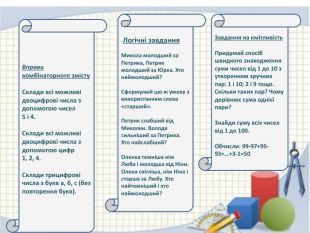
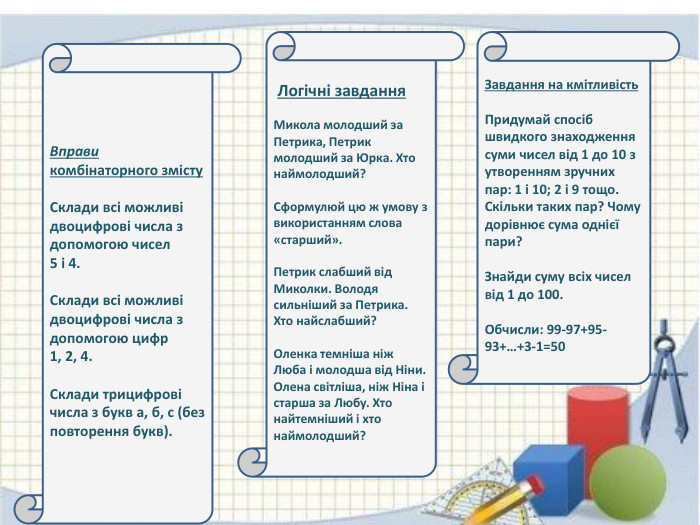
Логічні завдання. Микола молодший за Петрика, Петрик молодший за Юрка. Хто наймолодший? Сформулюй цю ж умову з використанням слова «старший». Петрик слабший від Миколки. Володя сильніший за Петрика. Хто найслабший?Оленка темніша ніж Люба і молодша від Ніни. Олена світліша, ніж Ніна і старша за Любу. Хто найтемніший і хто наймолодший?Завдання на кмітливість. Придумай спосіб швидкого знаходження суми чисел від 1 до 10 з утворенням зручних пар: 1 і 10; 2 і 9 тощо. Скільки таких пар? Чому дорівнює сума однієї пари?Знайди суму всіх чисел від 1 до 100. Обчисли: 99-97+95-93+…+3-1=50 Вправи комбінаторного змісту. Склади всі можливі двоцифрові числа з допомогою чисел 5 і 4. Склади всі можливі двоцифрові числа з допомогою цифр 1, 2, 4. Склади трицифрові числа з букв а, б, с (без повторення букв).

Вправи на дослідження. Як зміниться частка, якщо ділене і дільник збільшити (зменшити) в 3 рази? (( За потреби добери конкретні приклади). Як зміниться частка, якщо ділене збільшити в 3 рази, дільник зменшити в 4 рази?Як зміниться частка, якщо ділене зменшити в z разів, а дільник збільшити в r разів?Завдання, в яких треба враховувати положення точки або просторове розміщення предметів. Від дерева хлопчик пробіг 20 метрів, а потім повернувся і пробіг у протилежному напрямі 35 метрів. На якій відстані від дерева він зупинився?Три лелеки стали в один ряд. Відстань між сусідами лелеками 9 метрів. Яка відстань між крайніми лелеками? Задачі-жарти. Брат з’їв 4 сливи, а сестра 3. Скільки слив з’їла їхня бабуся?На груші росло 60 груш, а на вербі на 12 груш менше. Скільки груш росло на вербі?Сестра старша від брата на 7 років. На скільки років вона буде старша за брата через 3 роки?Чотири хлопчики вирушили з міста в село, а назустріч ім. – троє дівчаток. Скільки йшло дітей з міста в село?Троє коней за годину пробігли 15 км. Скільки км пробіг кожен кінь?

Залучаючи здібних учнів до розв’язання нестандартних вправ, ми тим самим інтенсифікуємо навчання, розвиваємо творче мислення школярів, прищеплюємо стійкий інтерес до предмета. Що є запорукою успішного його вивчення у середніх та старших класах. Однак слід пам’ятати, що така робота буде ефективною тільки за умов доброзичливого ставлення до кожного здобувача освіти, заохочення його до висловлювання різних ідей постановки найрізноманітніших запитань. ДЯКУЮ!