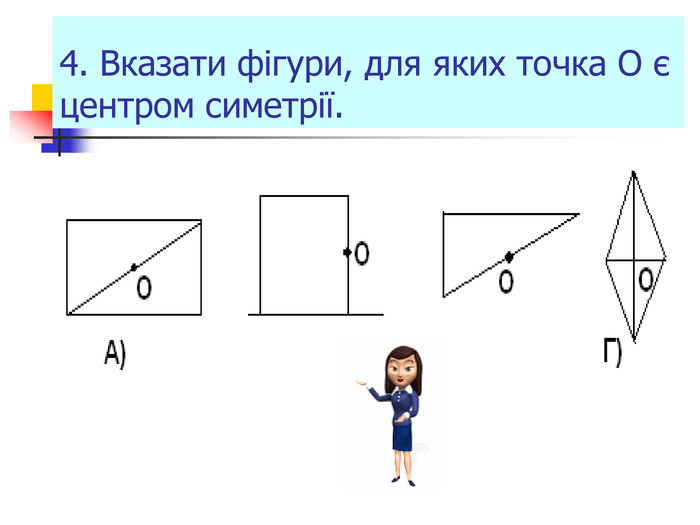
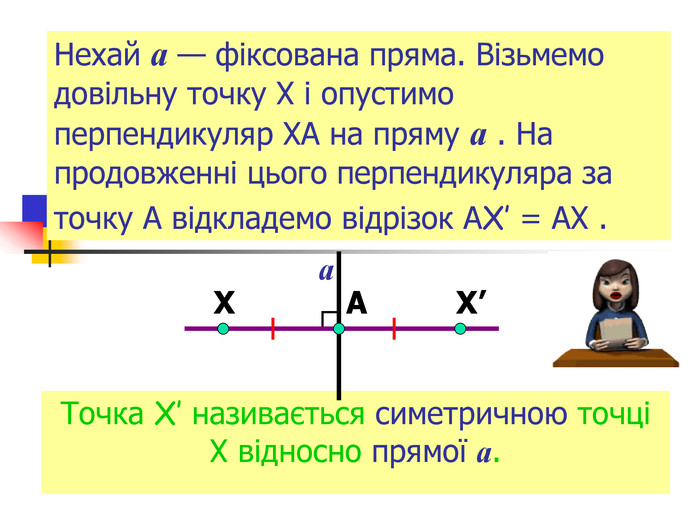
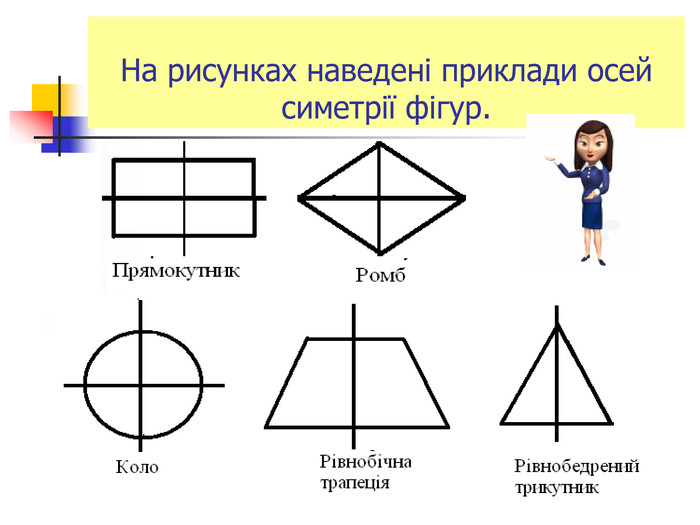
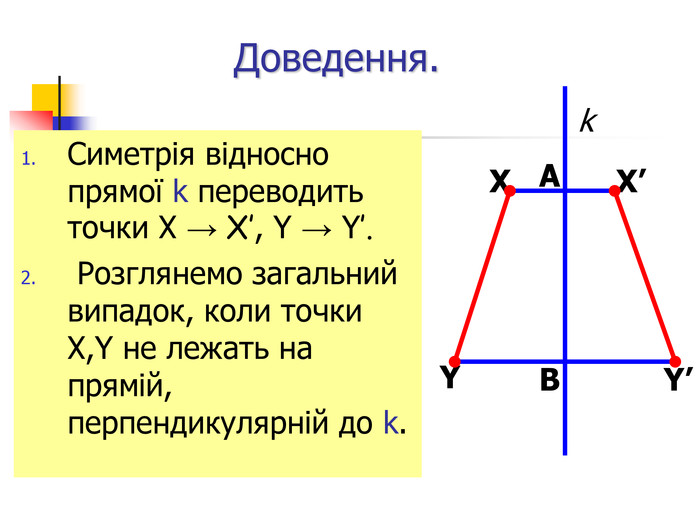
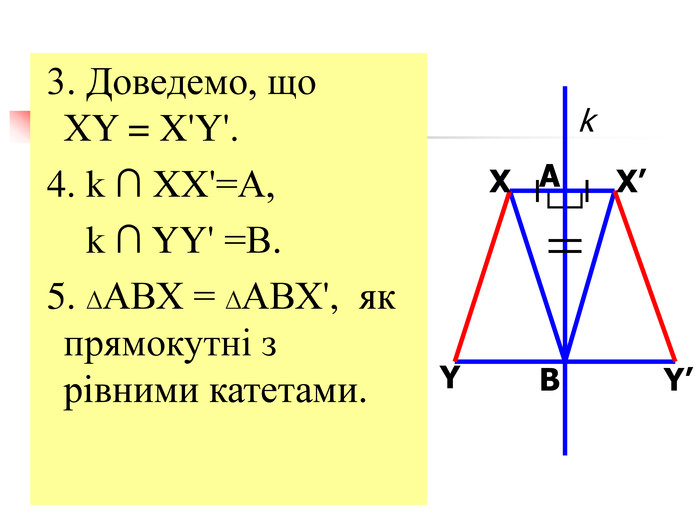
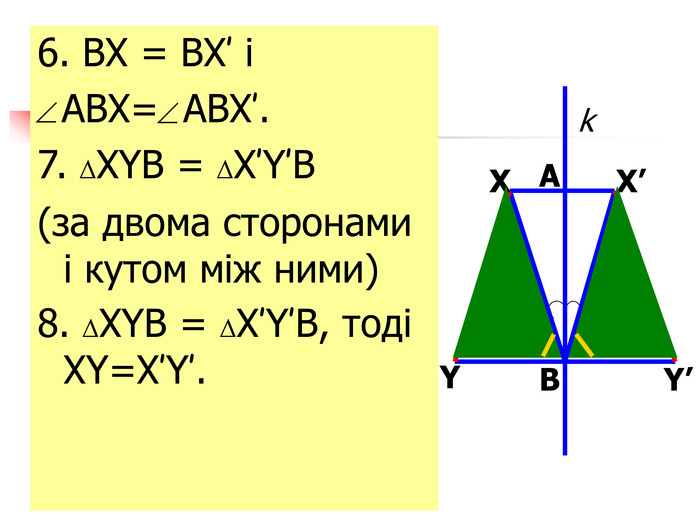
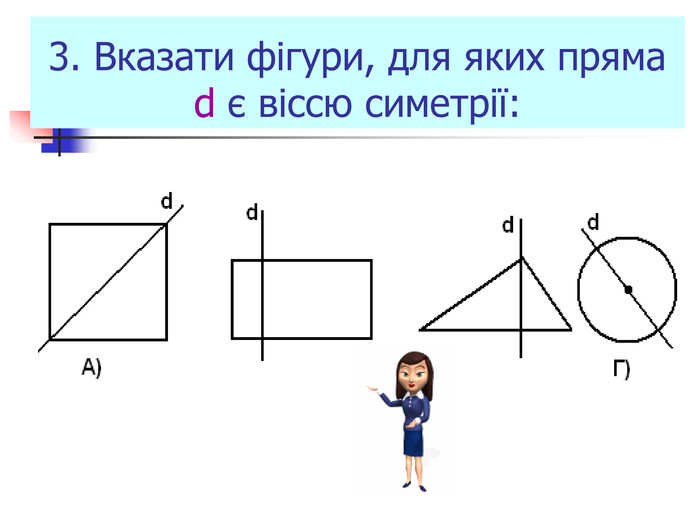
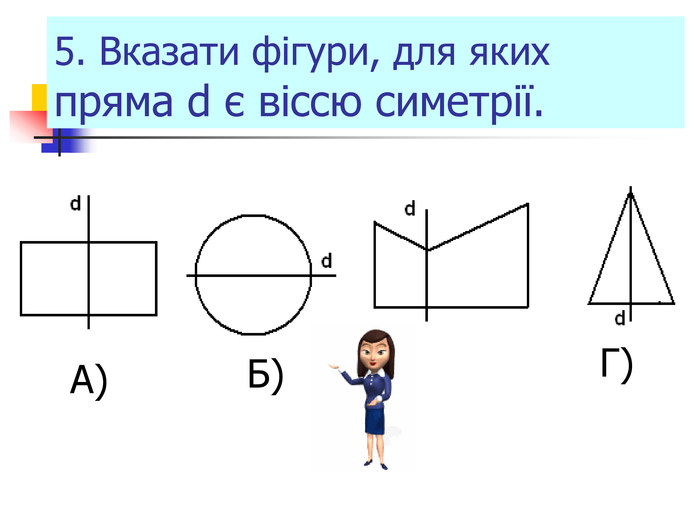
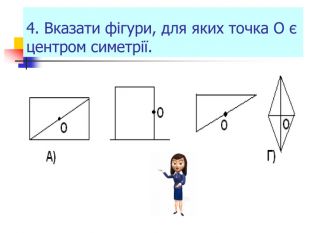
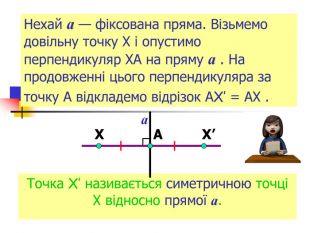
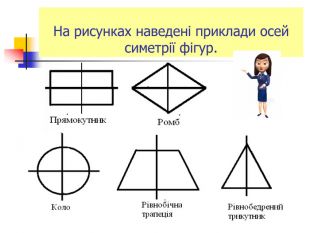
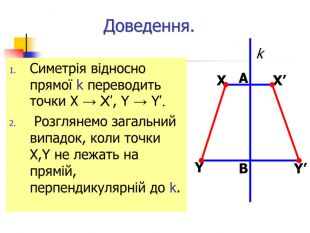
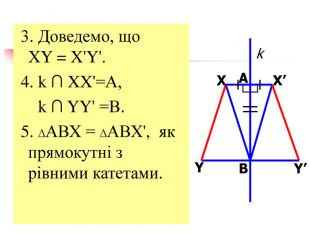
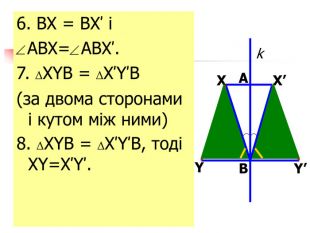
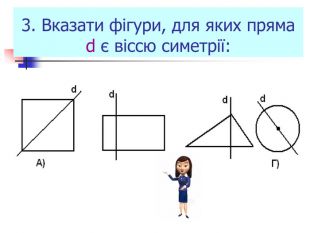
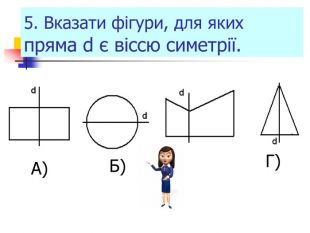
Презентація "Симетрія"
Про матеріал
Презентація "Симетрія" передбачає виробленню в учнів умінь самостійно здобувати і застосовувати знання, тобто самостійно вчитися Учні також зможуть перевірити свої знання,виконавши тестові завдання. Сподіваюся, що цей матеріал принесе користь учителю математики та учням. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Геометрія 9 клас (Бурда М.І., Тарасенкова Н.А.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку