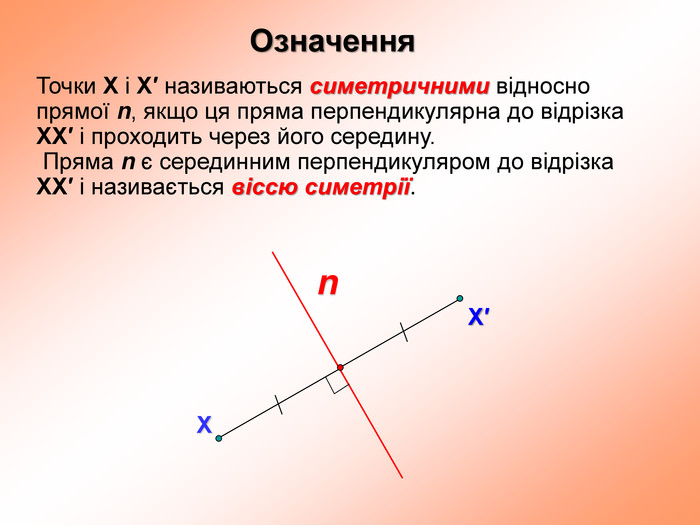
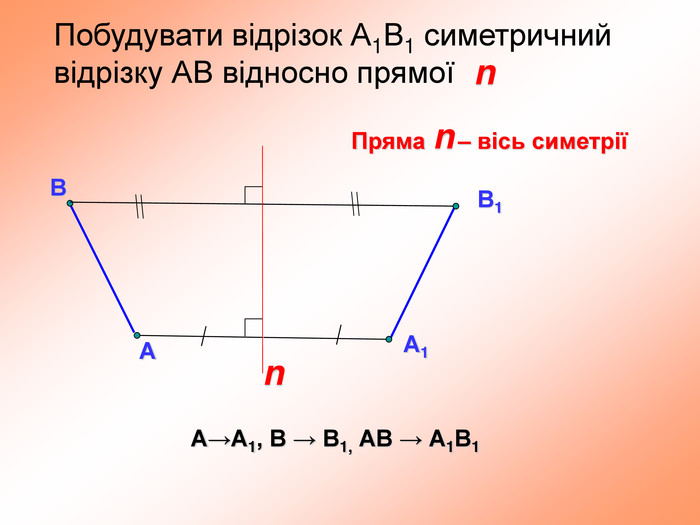
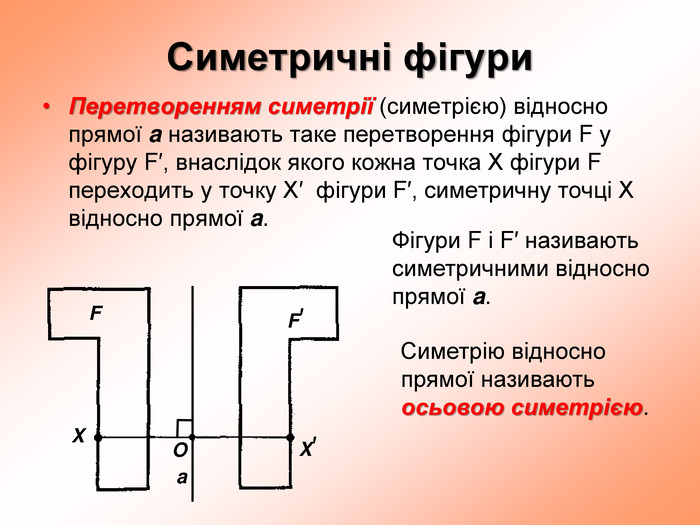
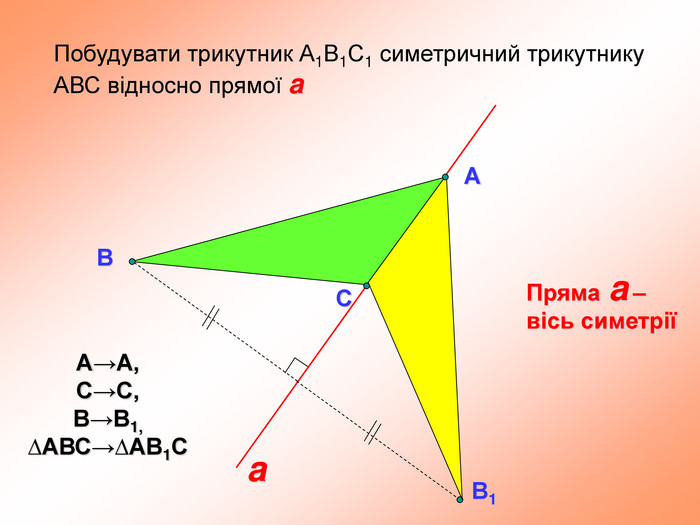
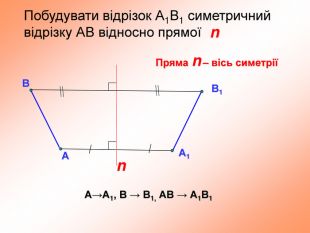
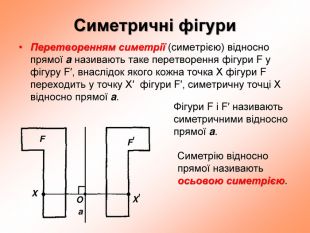
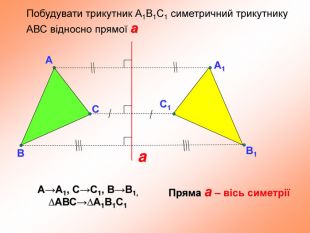
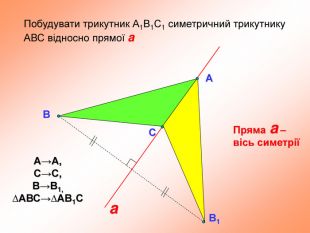
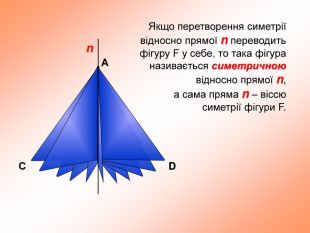
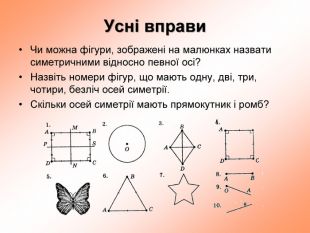
презентация "симметрия относительно прямой"
Про матеріал
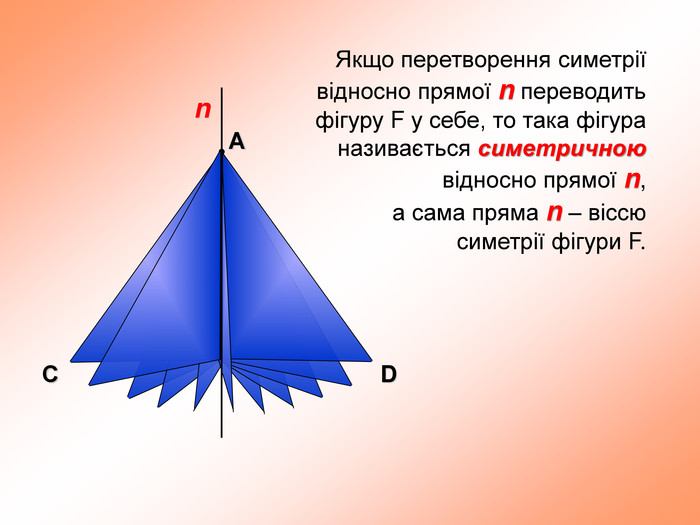
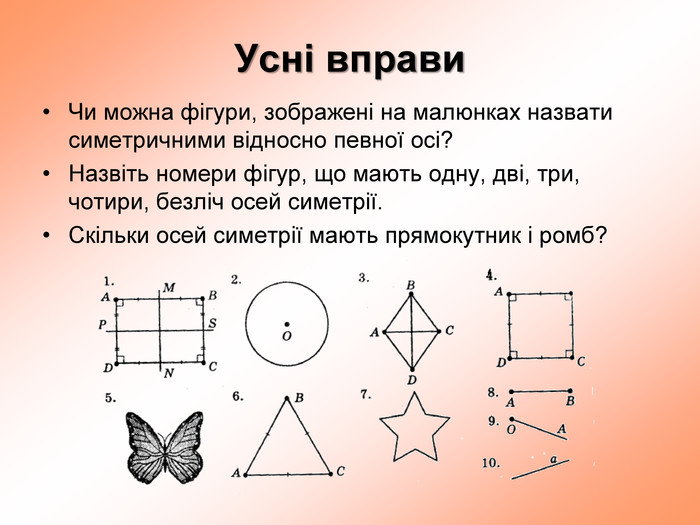
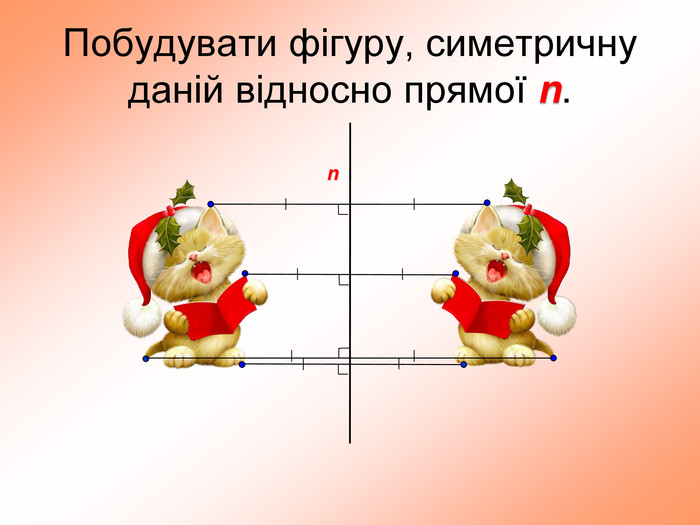
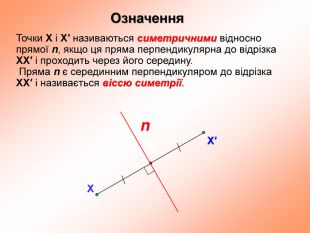
презентация поможет ученикам понять свойства осевой симметрии и послужит алгоритмом для решения задач при самостоятельном изучении темы во время карантина Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку