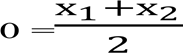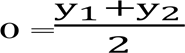Презентація. Тема:" Декартові координати на площині"
В даному матеріалі наведено приклад роботи учнів в групах. Завдання сприяють вивченю теоретичного матеріалу, формуванню навичок розв'язування задач та їх доведення.
Мета. Узагальнити та систематизувати знання учнів із теми: «Декартові координати на площині». Розвивати вміння міркувати, аналізувати та робити висновки. Сприяти самовихованню навичок спілкування, відповідальності в роботі з командою та самостійності в прийняті рішення.
|
Девіз уроку: « Необхідно, щоб той, хто що – небуть уміє, навчав цього інших, які мають у цьому потребу». (Альбрехт Дюрер) |
|
Микола Яругін: «І математика безмежно різноманітна і міститься в усьому». Ми з вами закінчуємо вивчення однієї з найцікавіших тем геометрії «Декартові координати на площині». Чому найцікавіших? Відповім так. Знання про координатну площину, властивості фігур на координатній площині допомагає в найнесподіваніші моменти. А деколи й рятує життя. Сайрес Сміт із твору Ж. Верна «Таємничий острів» своїми знаннями геометрії зумів визначити координати острова, де вони опинилися, і тим самим врятував життя своїм друзям. |
Сьогодні ви спробуєте на практиці застосувати свої знання.
Працює чотири команди: 1) «Теоретики», 2) «Практики», 3) «Дослідники», 4) «Філософи».
|
Запитання до команди «Теоретики». 1) Як знайти відстань між двома точками, якщо відомо їх координати? 2) Як знайти координати середини відрізка якщо відомо координати його кінців? 3) Що називають рівнянням фігури, заданої на площині ху? 4) Який вигляд має рівняння кола із центром у точці (a, b) і радіусом R? |
|
Команда «Практики». 1) Запишіть рівняння кола із центром у початку координат і радіусом R. 2) Запишіть рівняння прямої на площині ху. 3) Запишить рівняння: а) вертикальної прямої; б) невертикальної прямої. 4) Сформулюйте необхідну і достатню умовупаралельності двох невертикальних прямих на координатній площині. |
Команда «Дослідники» 1) У якому вигляді зручно записувати рівняння невертикальної прямої? 2) Що називають кутовим коефіцієнтом прямої?
3) У чому полягає суть методу координат?
4) Як можуть розміщені пряма і коло ?
Команда «Філософи»
1) Коли зародилася ідея координат?
2) Хто першим використав ідею координат? 3) У чиїх роботах була розкрита ідея координат?
4) Чому систему координат на площині називають декартовою?
|
Команда «Теоретики» 1) Які координати має середина відрізка АВ, якщо А (-6;7), В(4; -9)? 2) Чому дорівнює відстань між точками С(8;-11) і D(2; -3)? 3) Які координати має центр кола (х- 5)² + (у+9)² = 16 і чому дорівнює радіус кола? 4) Знайдіть центр і радіус кола,діаметром якого є відрізок МК, якщо М(14;12) і К(-10;2). |
Команда «Практики».
1) Чотирикутник ABCD- параллелограм.
Задано три його вершини: В(-2;3),С(10;9), D(7;0).Знайдіть координати вершини А
2) Які координати має точка осі ординат рівновіддалена від точок А(4;- 5) і В(2;3)?
3) Складіть рівняння прямої, яка проходитьчерез точки М (-2; -2) і N(2,10).
Команда «Дослідники» 1)Знайдіть координати точки перетину прямих 2х-5у=7 і –х+3у=12.
2) Доведіть, що коло (х+4)² +(у-1)² =13 і пряма х-у= - 4 перетинаються, і знайдіть координати точок їх перетину.
3) 
Доведіть, що дане рівняння х² +у² +6х -2у10=0 є рівнянням кола, і вкажіть координати центра та радіус цього кола.
Команда «Філософи»
1) Чому дорівнює кутовий коефіцієнт прямої; а) у=2х-7; б) у= -3х; в) у= х+5; г) у=32х; д) 5х-3у =7.
2) Серед даних прямих укажіть пари паралельних прямих: а) х-3у= -5; б) 3х+2у= 15; в)-2х+6у= -17; г) 8х-у= -19; д) 9х+6у=1.
3) 
Складіть рівняння прямої, яка проходить через точку К (2; -3) і паралельна прямій у=-3х+1.
IV Дуель капітанів Встановити відповідність:
|
Додаткове завдання: 1) Точки А (-3;5), В (2; 4) і С (1; 3) – вершини трикутника АВС. Складіть рівняння прямої, яка містить медіану ВМ трикутника АВС. 2) Знайдіть довжину хорди кола (х+1)² +(у2)² =25, яка лежить на прямій у =3х. 3) Складіть рівняння кола, яке проходить через точку D (-8; -2), якщо центр кола належить осі ординат, а радіус дорівнює 10. |
|
Домашнє завдання Повторити: § 8-11. Розв’язати: № 1-5, 7, 8, 11, 12. Молодці! Пам’ятайте: «Вчитися можна тільки весело… Щоб перетравлювати знання, потрібно поглинати їх з апетитом». (Анатоль Франс) |
|
Теоретики 1) АВ = 2) х 3) Рівняння фігури – рівняння з двома змінними ху, яке має властивості: а) якщо точка € F, то її координати є розв’язком рівняння; б) будь- який розв’язок (х;у) даного рівняння є координатами точки, яка належить фігурі F. 4) ( х- а)² + (у-в)² = R². 5) С(-1;-1). 6) АВ = 10. 7) А (5;-9); R= 4. 8) О (2;7) R= 4. |
Команда «Практики»
1) х² +у² = R². 2) ax +by = c.
3) 
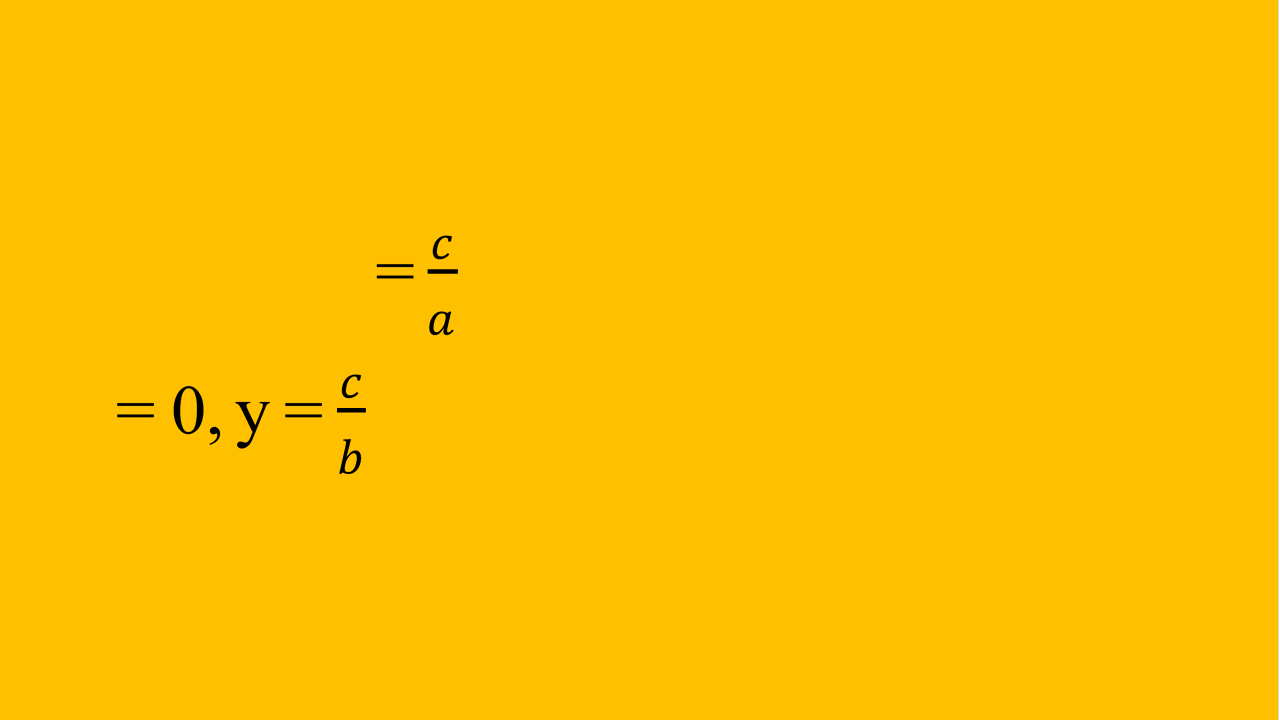b = 0, x – вертикальна пряма, a – невертикальна пряма.
4) 𝑘1 = 𝑘2 𝑏1 ≠ 𝑏2, 5)ОВД(2,5;1,5), А(-5;-6).
6)М (0; -1,75). 7) у = 3х + 4.
Команда «Дослідники»
1) у = кх+ в. 2) Кутовий коефіцієнт – к= тангенсу кута, утвореного прямою з додатним напрямом системи координат.
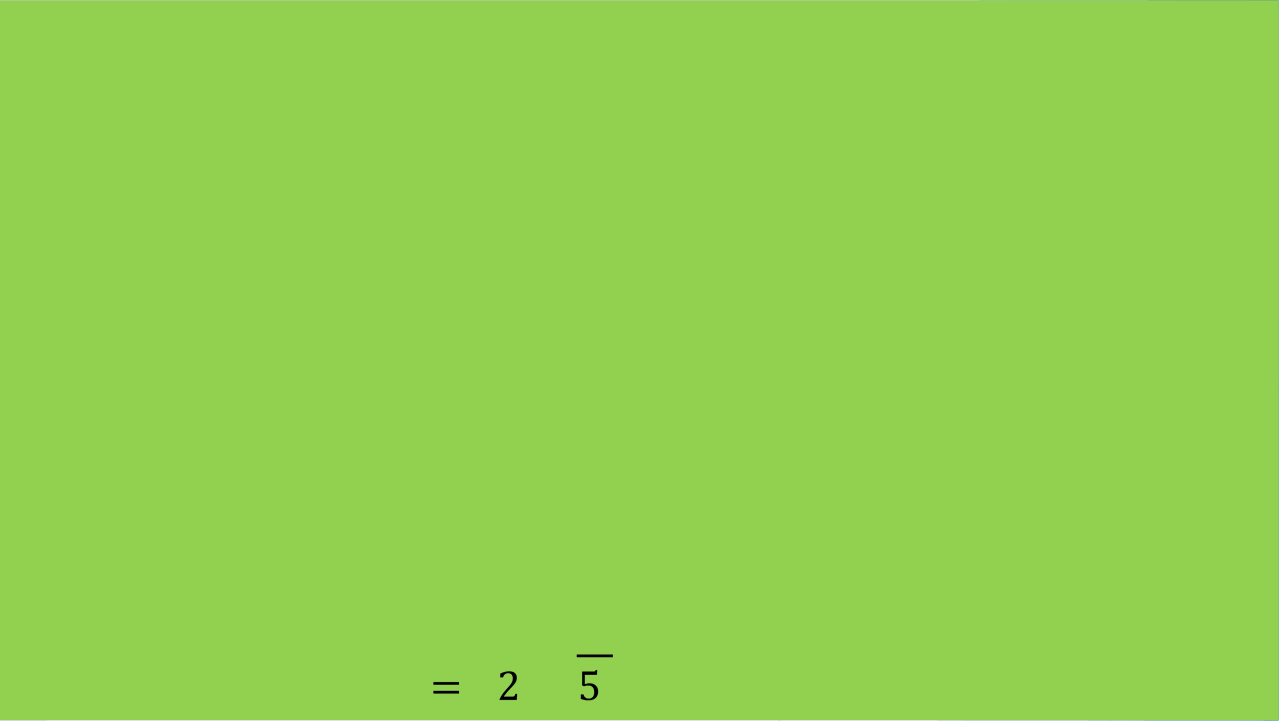3)Суть методу координат полягає в тому, що задача про пошук властивостей фігури зводиться до задачі про дослідження її рівняння. 4) Пряма і коло: а) перетинаються (дві спільні точки); б) пряма дотикається (одна спільна точка); в) не мають спільних точок.
5) (31; 81).6) (-6; -2), (-1; 3).
7) А(-3; 1), R .
Команда «Філософи»
1) У II ст. до н. е.
2) 
2) У II ст. до н. е. Гіппарх використав ідею координат для визначення місця розташування об’єктів на поверхні Землі.
3) Ідеї були розкриті в XVII ст. Ферма і Декартом.
1) На честь Рене Декарта.
2) а) к = 2, б) к = -3, в) к =1, г) к = -2, д) к =5.
3) 6) б) і д) к = - ; а) і в) к = - .
4) У = - 3х + 3.
Додаткове завдання: 1) М (-1; 4), у = 4.
2) А (1; 3), В (- .
3) х² + (у + 8 )² = 100.
про публікацію авторської розробки
Додати розробку