Презентація «Системы линейных уравнений с двумя переменными. Графический способ решения систем линейных уравнений с двумя п
Про матеріал
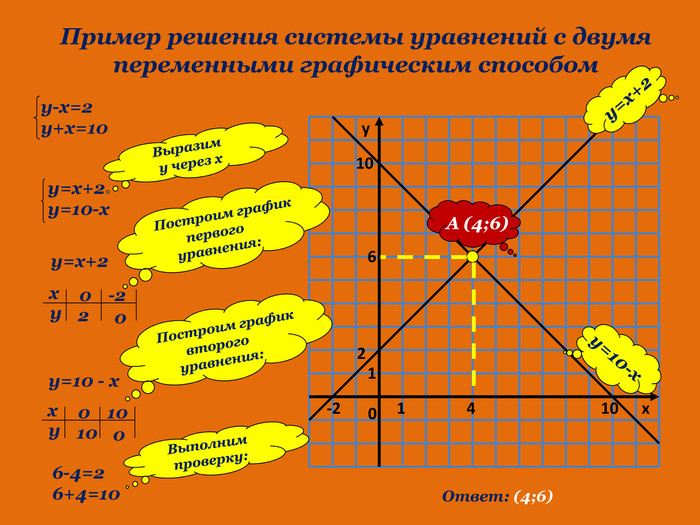
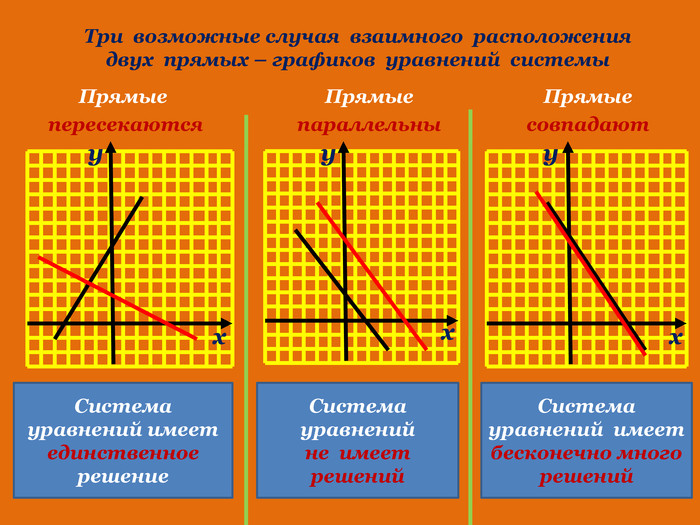
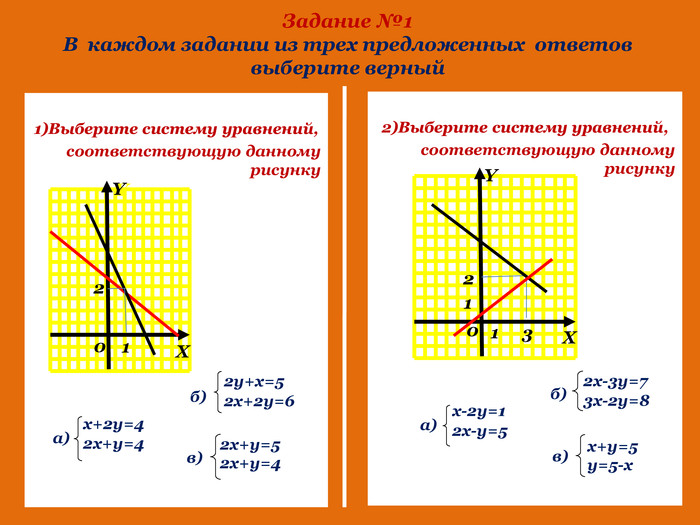
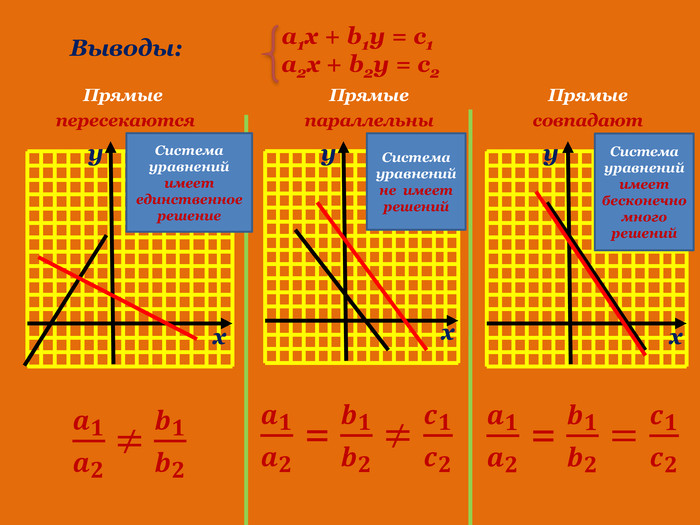
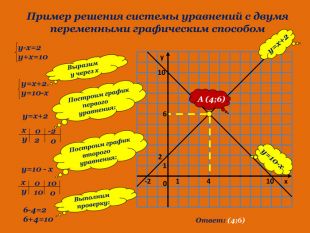
Презентація до розробки уроку алгебри в 7 класі на тему "Системи лінійних рівнянь з двома змінними. Розв язування систем двох лінійних рівнянь з двома змінними (за допомогою онлайн графічного калькулятора "DESMOS")
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Большое спасибо вам за работу. Очень лаконично и понятно!
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
Системи рівнянь із двома змінними Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку