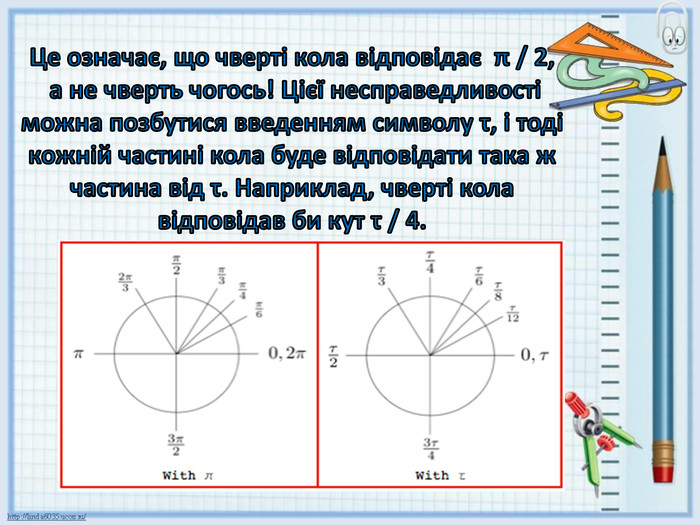
Презентація "Стала величина тау"
Про матеріал
Презентація для факультативного курсу з алгебри містить цікаву інформацію стосовно сталої величини «тау»
Презентацію можна використовувати під час проведення уроку з алгебри для 10-го класу на тему «Тригонометричні функції»
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
+12 балів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку








![«Якщо ви задаєте геометричну постійну кола через відношення довжини кола до діаметру, то це не що інше як поділ її на подвоєний радіус, і ця [додатково введена] двійка переслідуватиме вас впродовж всіх обчислень», - продовжує він. «Якщо ви задаєте геометричну постійну кола через відношення довжини кола до діаметру, то це не що інше як поділ її на подвоєний радіус, і ця [додатково введена] двійка переслідуватиме вас впродовж всіх обчислень», - продовжує він.](/uploads/files/487/9161/9251_images/8.jpg)