УРОК-КЕЙС «ТРИГОНОМЕТРІЯ»

Автор кейса: Шарабурова О. О.

Рівень (клас): 10

Тема: Тригонометричні формули

Мета уроку:

Дидактична:

-         Формувати в учнів систему практичних і наукових знань, умінь        та        навичок             з          теми тригонометричні   формули, зокрема, засвоєння й закріплення основних математичних формул,

виведення нових формул множення тригонометричних функцій, повторення законів, теорій та правил, наукових понять з фізики, астрономії,     біології         та             інших             навчальних             дисциплін, де використовується тригонометрія, із застосуванням вправ, задань і дидактичних матеріалів;

-         Систематизувати знання учнів з метою всебічного осмислення ними даної теми.

Розвивальна:

-         Навчитися аналізувати об’єкти, знаходити закономірності, робити самостійні висновки з прочитаного та побаченого;

-         Вдосконалювати, розвивати уміння та навички щодо розв’язання задач на застосування тригонометричних формул;

-         Продовжити роботу з розвитку логічного мислення, математичної мови та пам’яті, математичного аналізу та синтезу. 

Виховна:

-         Продовжити формування навичок естетичного оформлення записів у зошитах;

-         Привчати до вміння спілкуватися та вислуховувати інших;

-         Виховувати свідому дисципліну;

-         Розвивати творчу самостійність та ініціативу;

-         Стимулювати мотивацію та інтерес до вивчення тригонометрії. 

 

Розгортка за предметами:

 

Історія

Астрономія

Фізика

Біологія

Музичне виховання

Фізична культура

Креслення

Алгебра

 

Вступ.

 

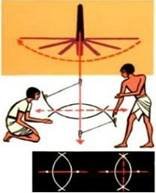
Тригонометрія виникла з практичних потреб людини. За її допомогою ще з давніх часів люди визначали відстань до недосяжних предметів, складали географічні карти, здійснювали виміри землі та розрахунки у будівництві. Тобто тригонометрія у своєму базовому стані носила геометричний характер. Згодом тригонометрія набувала аналітичного наповнення та тригонометричні залежності стали розглядати як функції.

 

Історія

 

Історія тригонометрії бере початок у Стародавній Греції більш ніж 3000 років тому.

Одним з найважливіших досягнень тих часів є визначення співвідношення катетів і гіпотенузи в прямокутних трикутниках, яке пізніше отримало назву теореми Піфагора.

 

Історія розвитку тригонометрії у Стародавній Греції пов’язана з ім’ям астронома Клавдія Птоломея – автора геоцентричної системи світу до Коперника. Грекам не були відомі синуси, косинуси й тангенси. Вони користувалися таблицями, які дозволяли знаходити значення хорди кола за допомогою дуги, якою вона стягувалася. Одиницями для виміру хорди були градуси, хвилини й секунди. Один градус прирівнювався до одної шістдесятої радіусу.

Також  дослідження древніх греків просунули розвиток сферичної тригонометрії. Зокрема, Евклід у своїх «Початках» приводить теорему про закономірності співвідношень об’ємів куль різного діаметра. Його праці в цій галузі стали своєрідним поштовхом у розвитку ще і суміжних галузей знань. Це, зокрема, технологія астрономічних приладів, теорія картографічних проекцій, система небесних координат і т.і.

У IV столітті центр розвитку математики перемістився в Індію. Індійські математики були першими у застосуванні тригонометрії для астрономічних розрахунків.

Історія виникнення тригонометрії як відокремленого розділу математичного навчання почалася в Середньовіччі. Саме тоді вчені замінили хорди синусами. Це відкриття дозволило ввести функції, що стосуються дослідження сторін і кутів прямокутного трикутника. Тобто саме тоді тригонометрія почала відокремлюватися від астрономії, перетворюючись в розділ математики. Перші таблиці синусів були в Аріабхати, вони були проведені через 3⁰, 4⁰, 5⁰.

 

 

Пізніше      з'явилися     докладні      варіанти       таблиць, зокрема, Бхаськара привів таблицю синусів через 1⁰.

 

 

 

 

Історія тригонометрії в Європі почалася у XII столітті та пов'язана з ім'ям англійця Річарда Уоллінгфордского, який став автором твору «Чотири трактати про прямих і звернених хордах».

До XV століття багато авторів у своїх працях згадують про тригонометричні функції. Тому в другій половині XVI століття ця тема зацікавила багатьох видатних людей того часу, в тому числі Миколу Коперника, Йоганна Кеплера, Франсуа Вієта.

 

Коперник відвів тригонометрії кілька глав свого трактату «Про обертання небесних сфер» (1543). Трохи пізніше, в 60-х роках XVI століття, Ретик – учень Коперника – приводить в своїй праці «Оптична частина астрономії» п’ятнадцятизначні тригонометричні таблиці.

 

                                                                Франсуа      Вієт     в     «Математичному

каноні» (1579) дає ґрунтовну і систематичну, хоча і бездоказову, характеристику пласкої та сферичної тригонометрії.

 

Додання тригонометрії сучасного змісту і виду стало заслугою Леонарда Ейлера. Його трактат «Введення в аналіз нескінченних» (1748) містить визначення терміна «тригонометричні функції», яке еквівалентно сучасному. Таким чином, цей вчений зміг визначити зворотні функції. Але і це ще не все. Визначення тригонометричних функцій на всій числовій прямій стало можливим завдяки дослідженням Ейлера не тільки допустимих негативних

кутів, але і кутів більших за 360⁰. Саме він в своїх роботах вперше довів, що косинус і тангенс прямого кута негативні. Розкладання цілих ступенів косинуса і синуса теж стало заслугою цього вченого. Загальна теорія тригонометричних рядів і вивчення збіжності отриманих рядів не були об'єктами досліджень Ейлера. Однак, працюючи над вирішенням суміжних завдань, він зробив багато відкриттів в цій області. Саме завдяки його роботам продовжилась історія тригонометрії.

 

 

Завдання:

Знайдіть    та        ознайомтеся          з          історією        появи            назв   основних тригонометричних функцій  cos, sin, tg, ctg.

Астрономія

 

Необхідність у розв’язанні трикутників раніш за все виявилася в астрономії. Тому протягом довгого часу тригонометрія вивчалася й розвивалася як один з розділів астрономії.

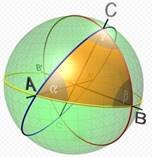
На будь-якій кулі, як і на поверхні Землі, відстані між точками можна розраховувати за кутами, під якими їх видно з центра кулі. 

 

 

Задачу про визначення усіх елементів, так званих, сферичних трикутників розв’язав Франсуа Вієт.

 

За правилами сферичної тригонометрії здійснюється перетворення азимутальних і екваторіальних координат. У сучасній математиці ці перетворення координат описуються матрицями перетворень.

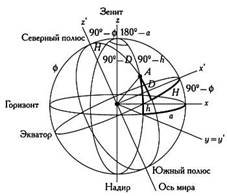На ілюстрації положення зірки А визначається вектором, три складові якого визначаються проекціями зірки на площину горизонту (площину ху) і вісь зеніт-надир (вісь z). Таким чином, положення зірки задається трьома координатами: х, у, z.

Отже, в горизонтальних координатах положення зірки А можна визначити як вектор

(r • cos(h) • cos(a), r • cos(h) • sin(a), r • sin(h)).

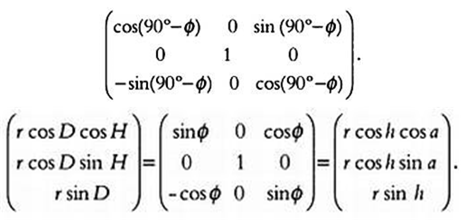Аналогічно визначається положення зірки щодо небесного екватора (площини x'y') та осі світу (осі z'), тобто осей екваторіальних координат х'у'z': (r • cos(D) • cos(H), r • cos(D) • sin(H), r • sin(D)). Як показано на попередньому малюнку, ми можемо перейти від координат х, у, z до координат х'у'z 'всього лише виконавши поворот щодо осі у, яка збігається з віссю у' на кут (90⁰-ф), де ф - широта. У результаті х перейде у вісь х' вісь z - у вісь z'. Матриця перетворень щодо другої осі (осі у=у ') для кута (90⁰-ф) записується так:

 

 

 

 

 

 

маємо

 

 

 

Отже, формули перетворення координат записуються так:

 

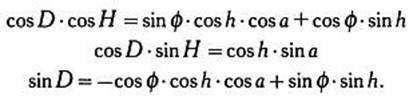
Ті ж співвідношення, що виводяться за допомогою матриці перетворень, можна отримати за формулами сферичної тригонометрії Бесселя, розглянувши трикутник «полюс-зеніт-зірка».

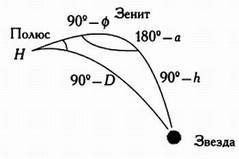Сферичний трикутник «полюс-зеніт-зірка» як і    раніше          широко             використовується             в сферичній або позиційній астрономії, так як він містить всю інформацію, представлену на попередній ілюстрації. Слід враховувати, що сторонами цього трикутника є дуги великого кола небесної сфери. Отже, їх довжина вимірюється в градусах, однак, за традицією,

часовий кут і пряме сходження відраховуються в годинах, хвилинах і секундах. Перейти від годин до градусів дуже просто - достатньо врахувати, що 360⁰ еквівалентні 24 годинам або, що аналогічно, 15⁰ еквівалентні 1 годині.

 

Завдання: Горизонтальний паралакс Сонця 8,794´´, а видимий кутовий діаметр Сонця дорівнює 32´02´´. У скільки разів радіус Сонця більший за радіус Землі?

 

Фізика

 

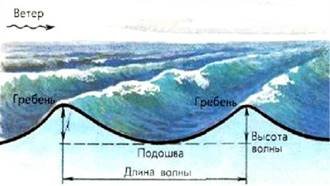Розглядаючи графіки тригонометричних функцій, можна згадати, що в повсякденному житті      є          схожі криві.

Наприклад, хвилі на морі мають      форму,          що      нагадує синусоїду. І це не випадково, бо багато      фізичних      величин періодично змінюються і можуть бути описані         за        допомогою тригонометричних функцій.

 

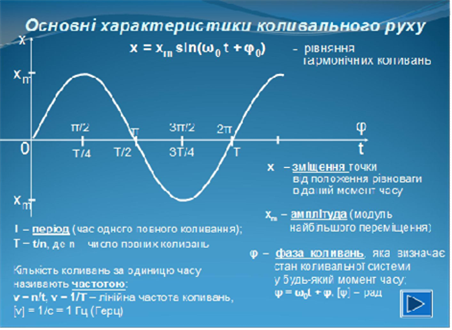
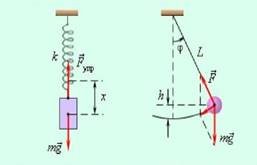Коливання – найпоширеніша форма руху в навколишньому світі    та        техніці. Коливаються дерева, хвилі під дією вітру, поршні у двигуні автомобіля тощо.

 

Прикладами простих коливальних систем можуть слугувати вантаж на пружині або математичний маятник.

 

Коливання, при яких змінення фізичних величин здійснюються за законами косинуса чи синуса, називаються гармонічними коливаннями.

Фізика це наука про природу. Але вона не може існувати без математики. Мудрі слова сказав Галілео Галілей: “ Велика книга природи написана на мові математики ”.

Сьогодні ми можемо сказати, що багато природних явищ написані на мові тригонометричних рівнянь.

Як виникає веселка? Північне сяйво? За яким графіком рухається Сонце?

Як тригонометрія може допомогти знайти відповіді на ці питання? ».

 

Вперше теорія веселки була дана в 1637 році Рене Декартом. Він пояснив веселку, як явище, пов'язане з відображенням і заломленням світла в дощових краплях.

                                                                                                                                                       =      ,

                                                                                               де              = 1,        ≈ 1,33         -        відповідно

показники                     заломлення                     повітря                     і                      води, 

− кут падіння,               − кут заломлення світла.

 

Проникнення          у          верхні           шари атмосфери Землі заряджених частинок сонячного вітру визначається взаємодією магнітного поля планети з сонячним вітром і називається Північним сяйвом.

Сила, що діє на рухому в магнітному полі заряджену частинку називається силою Лоренца. Вона

пропорційна заряду частинки і векторному добутку поля і швидкості руху частинки.

F=qvBsin – сила Лоренца, де q - заряд; v – швидкість заряду; B – магнітна індукція;  кут між векторами v та B.

 

Видимий рух Сонця відносно горизонту протягом дня також відбувається за законом синуса. А який графік відтворює положення Сонця на початку сходу й наприкінці його заходу у перший день кожного місяця протягом року?

 

 

Завдання: За допомогою відривного календаря побудуйте графіки сходу та заходу Сонця за даними на перше число кожного місяця протягом будь-якого року. На вісі у відкладайте час сходу (заходу) Сонця, на вісі х – місяць року.

 

Дуже влучно усі періодичні процеси у природі описав у своєму вірші наш земляк, автор підручників з математики, алгебри та геометрії Григорій Петрович Бевз.

 

Зима за літом, ніч за днем. Плюс змінюється мінусом,

Все у природі і в людей йде за законом синуса.

То вверх крокуємо, то вниз, удачі за невдачами,

По синусоїді кудись всі пливемо неначе ми.

 

Завдання:

Розв’яжіть задачі.

 

1) 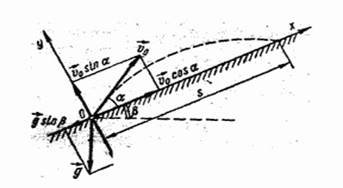           Камінь кинули на схилі гори під кутом α до її поверхні. Визначте     дальність             польоту каменя,   якщо початкова швидкість каменю дорівнює v₀, кут нахилу гори до горизонту β.

Опір повітря не враховувати.

 

 

 

2)            М’ячик кидають під гострим кутом до пласкої горизонтальної поверхні землі. Відстань, яку пролітає м’ячик, розраховується за по формулою L = v₀²/gsin2 (м), де v₀ = 11 м/c - початкова швидкість м’яча, а g - прискорення вільного падіння (g = 10 м/c). При якому найменшому значенні кута  (у градусах) м’яч перелетить річку завширшки 6,05 м?

 

3)            Катер повинен перетнути річку завширшки  70 м (L) та зі швидкістю течії  v = 0,5 м/c так, щоб причалити точно навпроти місця відправлення. Катер може рухатися з різними швидкостями, при цьому час у дорозі (у секундах) визначається виразом t = L/vctg, де гострий кут між напрямом руху катера та берегом відправлення. Під яким мінімальним кутом (у градусах) треба йти катеру, аби час у дорозі був не більше 140 c?

 

 

Біологія

 

 

Рухи у тваринному світі відбуваються за законом синуса. Крила птахів, хвости китів, тіло змії рухаючись, відтворюють графік синусоїди.

 

 

Завдання:

Наведіть інші приклади процесів у тваринному світі, які можна описати за допомогою тригонометрії.

 

Згідно з теорією «трьох головних людських біоритмів», кожна людина поєднує в собі набір різних біоритмів: інтелектуальний, емоційний та фізичний. Усі біоритми стартують одночасно в момент народження і відразу ж починають рости, потім зменшуються, потім знову ростуть, періодично повертаючись до початкового значення. Усі зміни відбуваються для всіх біоритмів періодично, але не синхронно. 

Інтелект, емоції та фізичний стан людини є періодичними процесами, вони мають безпосередній зв‘язок з тригонометрією.

 

Інтелектуальний ритм має період 33 дні і керує пам'яттю, здатністю до навчання, розумовою активністю, ясністю мислення.

 

Емоційний ритм триває 28 днів і впливає на почуття, настрій, емоції, душевність. 

 

Фізичний ритм складає 23 дні. Він регулює фізичну активність, силу, швидкість, координацію, опір хворобам, витривалість.

 

 

 

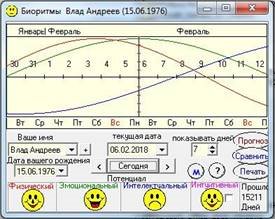
Завдання:

Скачайте програму з будь-якого сайту в Інтернеті, скористайтеся графіками власного біологічного ритму для визначення періодів найкращої загальної власної форми, коли збігаються інтелектуальний, емоційний та фізичний ритми.

 

У результаті дослідження, проведеного студентом іранського університету Шираз Вахидом-Резою Аббасі, медики вперше отримали можливість упорядкувати інформацію, що відноситься до електричної активності серця або, іншими словами, електрокардіографії.

Формула, яка отримала назву тегеранської, була представлена широкій науковій       громадськості        на       14-й конференції географічної медицини і потім — на 28-й конференції з питань застосування комп’ютерної техніки в кардіології, що відбулася в Нідерландах.  Ця формула являє собою комплексне алгебраїчно-тригонометричне рівняння, що складається з 8 виразів, 32 коефіцієнтів і 33 основних параметрів, включаючи кілька додаткових для розрахунків у випадках аритмії. Як стверджують медики, ця формула в значній мірі полегшує процес опису основних параметрів діяльності серця, прискорюючи тим самим постановку діагнозу і початок власне лікування.

 

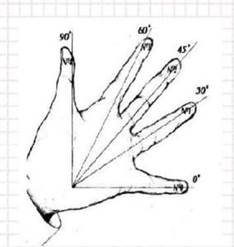Дуже часто виникає потреба у знанні напам’ять значення cos, sin, tg, ctg для кутів 0⁰, 30⁰, 45⁰, 60⁰, 90⁰.

Якщо провести лінії, як показано на малюнку, через мізинець та великий палець, то вони перехрестяться у точці, яка називається «місячний бугор». Утворюється кут 90⁰. Лінія мізинця утворює кут 0⁰, а промені, проведені з «місячного бугра» через безіменний, середній та вказівний пальці, утворюють кути 30⁰, 45⁰ та 60⁰ відповідно.

 

Треба запам’ятати лише одну формулу

  , де n – номер відповідного пальця:

мізинець – 0; безіменний – 1; середній – 2; вказівний – 3; великий – 4.

 

 

 

 

 

 

 

 

 

 

 

№ пальця	Кут 	Значення sin
0	00
1	300
2	450
3	600
4	900

                                                                                                 2                       

 

Завдання:

Користуючись наведеною інформацією складіть аналогічну таблицю занчень для cosвраховуючи його сутність.

 

Музичне виховання

 

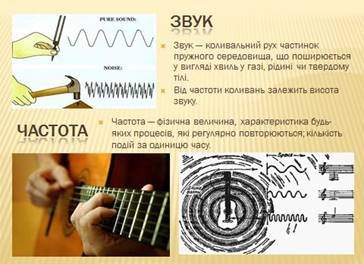Гармонічні коливання можна спостерігати слухаючи музику, адже при цьому в повітрі утворюються звукові хвилі; граючи на гітарі, бо струна          набуває        форми, близької до синусоїди.

 

Завдання:

Дайте відповідь.

Як        коливається            вушна мембрана слухача         під впливом звуку камертону?

 

 

Фізична культура

 

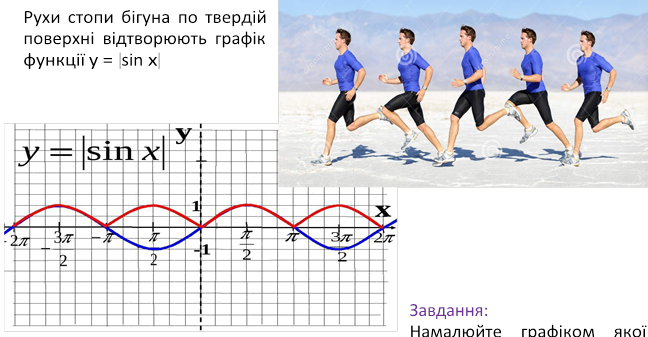
функції можна відобразити рухи п’ятки бігуна по воді; по гумі; по паралону завтовшки 30 см.

 

 

Креслення

 

Для того, щоб створити таки елегантні форми архітекторам та

 

 

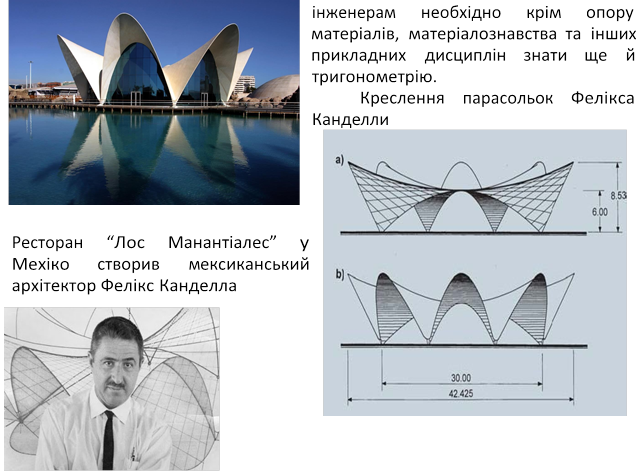
Виноробня у місті Логроньо провинції Ла Риоха

 

Іспанський архітектор

Сант’яго Калатрава

 

Океанографічний парк у Валенсії

 

Високошвидкісна залізнична станція

в Реджо-Емілія, Італія

 

Завдання: Графіки яких функцій використовували архітектори у розрахунках об’єктів, зображених на фотографіях?

 

Алгебра

 

Домашнім             завданням на       цей     урок   було   виконання   вправ математичного тренажеру.

Тренажер «Перетворення тригонометричних виразів»

1.Спростити вираз:

  1) 1 – cos²                                              2) sin²- 1

  3) cos² + ( 1 – sin²)                             4)  sin²+ 2 cos²- 1

  5) ( 1 - sin)(1 + sin) 6)  (cos- 1)( cos+1)

  7) 1 - sin² - cos²                                  8)  cos² - (1 - 2 sin²)  

  9) sin cos tq 10)   sin cos ctq  - 1

11) sin²+  cos²+tq²                            12)  tq ctq + ctq²

                             1sin                                                                           1                1

13)    tq 14)            cos    1cos 1cos

2.Доведіть, що при усіх допустимих значеннях , значення виразу не залежить від:

                          1 2cossin                                                           sin²cos²1

                1)    ₂ 2)    ₂

                          (sin cos)                                                                    sin 

                               1                1                                                         1sin 1sin

                3)             ₂              ₂            4)                               

                            1 tq  1 ctq                                                          cos cos

5) (sin+cos)² – 2sincos                 6) sin⁴+ cos⁴+2sin²cos²

                             2sin²cos²                                                        sin⁴cos⁴

                7) _{2                                              2}                               8) _{2                     2}                           

                             3sin 3cos                                                          sin cos 

3. Доведіть тотожність:            

1)    (sin+sin)(sin- sin) – (cos+cos)( cos- cos) = 0

2)    ctq² - cos² = ctq² cos²

                                   cos²sin² _{2                        2}                                         14sin²cos²

3)    _{2 2} = sin cos                 6) ₂ +2sincos= 1 ctq tq       (sin cos)

                            cos³sin³                                                                       _{2                              2}             2

4)     = cos- sin                  7) (1+tq) + (1 - tq) =        ₂                       

                            1 sincos                                                                                                      cos 

                                    cos cos                                                        tq tq

5)    1sin 1sin= 2tq                      8) ctq ctq= tqtq

 

 

 

Давайте пригадаємо основні тригонометричні формули.

 

 

 

Як бачимо, формул багато. Чи потрібно їх усі запам’ятовувати? Ні, є інший шлях – через базові можна вивести інші.

Наприклад, подивіться як виводяться відомі вам формули синуса подвійного й потрійного кута.

 

Як одержати формули потрійного кута?

 Підставимо у формулу

sin(b)= sincosb cossinb b =2  Одержимо:

sin(2)= sincos2 cossin2 =sin(cos²   sin²) 2sincoscos =sin(1 sin²  sin²)

2sin(1 sin²)=sin  2sin³ 2sin  2sin³ = = 3sin  4sin³

 Отже:         sin3 = 3sin  4sin³

 

 

З тригонометричними функціями ми виконували віднімання й додавання. А як з іншими діями?

 

 

 

Як ви вважаєте, які формули для цього можна використати?

 

Виконаємо вивід цих формул.

 

sin(b) = sincosb+ cossinb

+ sin(b) = sincosb- cossinb

sincos= 1/2(sin( +sin())

 

cos(b) = coscosb - sinsinb

⁺ cos(b) = coscosb + sinsinb coscos =1/2(cos()+cos())

 

cos(b) = coscosb - sinsinb

^- cos(b) = coscosb + sinsinb coscos =1/2(cos()-cos())

 

Завдання:

Вивести формулу тангенса потрійного кута.

 

 

Підведення підсумків уроку

 

№	Найменування	Зміст
1	Результати уроку- кейсу можна доповнити такими знахідками учнів:
2	На допомогу учню та учителю:	http://edufuture.biz/index.php?title=Заглавная_страница
3	Джерела інформації для уроку-кейсу:	http://fb.ru/article/211382/istoriya-trigonometriivozniknovenie-i-razvitie; http://detectivebooks.ru/book/34458764/?page=19; https://studopedia.su/16_20719_trigonometriya-vastronomii.html; https://kopilkaurokov.ru/matematika/presentacii/uchiebnyiproiekt-trighonomietriia-v-okruzhaiushchiem-nas-mirie-izhizni-chielovieka; http://dariya228.eto-ya.com/5-2; http://dariya228.eto-ya.com/5-2; Власна презентація «Тригонометричні формули»
4	Локація проведення уроку-кейсу:	Урок-кейс проходить у навчальному кабінеті.
5	Домашнє завдання:	Виконати запропоновані завдання та підготувати запитання, які виникли в ході ознайомлення з уроком-кейсом.
6	Тривалість:	90 хвилин (спарений урок)
7	Отримані результати і напрацьовані компетенції:	-                      вміння швидко відшуковувати необхідну інформацію за темою; -                      вміння використовувати отриману інформацію з практичною метою; -                      засвоєння конкретних знань з алгебри, фізики та інших предметів, наведених у розгортці;
		- поглиблення полікультурної, інформаційної, комунікативної компетенцій.
8	Теги:	теорема Піфагора, тригонометрія, основні тригонометричні функції, графіки тригонометричних функцій, тригонометричні формули, сферична тригонометрія, трикутник «полюс-зеніт-зірка», надир, паралакс, вектор, проекція, механічні коливання, звукові хвилі, гармонічні коливання, заломлення світлового променя, Північне сяйво, теорія веселки, біоритми, формула серця.