Презентація "Статистика "

Математична статистика (з використанням Excel) . * *

Зміст

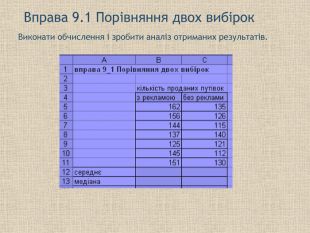
Урок 1 Основні поняття: статистика, статистичні дані, генеральна сукупність, вибірка, об'єм вибірки, якість вибірки. Практичне завдання Узагальнення отриманих знань і результатів виконання завдання

Основні поняття Математична статистика - це розділ математики, присвячений методам збору, аналізу і опрацювання статистичних даних для наукових и практичних цілей. В науку термін «статистика » ввів німецький учений Готфрід Ахенваль у 1746 році. Математична статистика досліджує масові явища, застосовується в соціології, економіці, психології на виробництві і т.д. Статистичні дані це дані, отримані в результаті обстеження великої кількості об'єктів чи явищ. Приклад : кількість тон пшениці, яку збирають з одного гектара по різних областях України надає можливість визначити, яка територія є найврожайнішою і т.д.

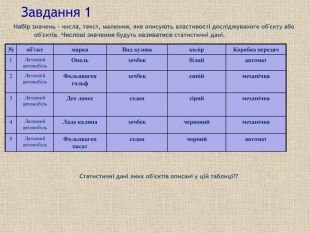
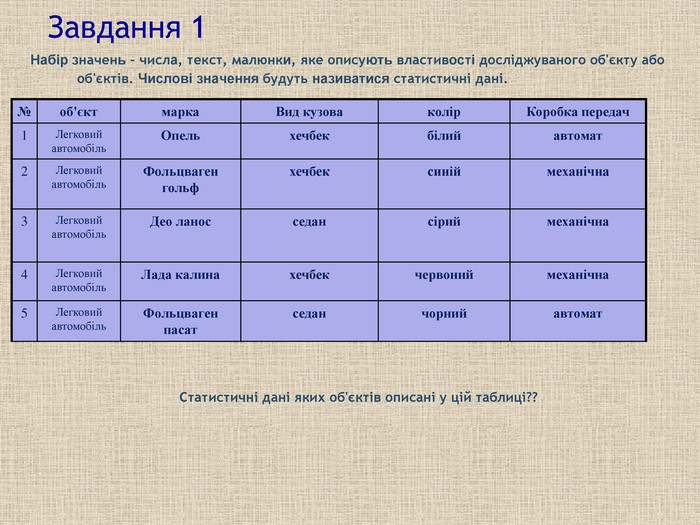
Завдання 1 Набір значень – числа, текст, малюнки, яке описують властивості досліджуваного об'єкту або об'єктів. Числові значення будуть називатися статистичні дані. № об'єкт марка Вид кузова колір Коробка передач 1 Легковий автомобіль Опель хечбек білий автомат 2 Легковий автомобіль Фольцваген гольф хечбек синій механічна 3 Легковий автомобіль Део ланос седан сірий механічна 4 Легковий автомобіль Лада калина хечбек червоний механічна 5 Легковий автомобіль Фольцваген пасат седан чорний автомат Статистичні дані яких об'єктів описані у цій таблиці??

Генеральна сукупність, вибірка Множина всіх об'єктів, які підлягають дослідженню, називається генеральною сукупністю, а підмножина випадково вибраних об'єктів(відібрана по конкретному правилу кількість об'єктів) із генеральної сукупності називається вибірковою сукупністю або просто вибіркою. Приклад генральної сукупності: Все населення України, учні Сл-Шаргородської школи, робітники підприємства «Склосталь» т.д. Приклад 2.1. Множина деталей виготовлених у цеху є скінченною генеральною сукупністю. Приклад 2.2. Множина можливих значень, які можна отримати у результаті вимірювання фізичної величини є нескінченною генеральною сукупністю Приклад 2.3.Множина усіх легкових автомобілів шаргородського району є генеральною сукупністю. А статистичні дані про легкові автомобілі з таблиці будемо називати вибіркою. Кожне значення вибірки називають варіантою

Об'єм вибірки, що це? Якщо для дослідження надаються статистичні дані про 50 однотипних об'єктів, то проводять дослідження над усіма об'єктами. Якщо для дослідження надаються статистичні дані про значно більшу кількість, для вибірки беруть 0,01% випадкових статистичних даних Приклад Якщо під час імпорту з трьох тисяч упаковок товару (генеральна сукупність) для контролю якості відібрали 300 упаковок (вибірка), то об'єм генеральної сукупності складає 3000, а об'єм вибірки –300. Тобто, число елементів вибірки називають об’ємом вибірки, а число елементів генеральної сукупності – об’ємом генеральної сукупності.

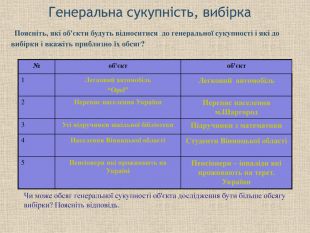
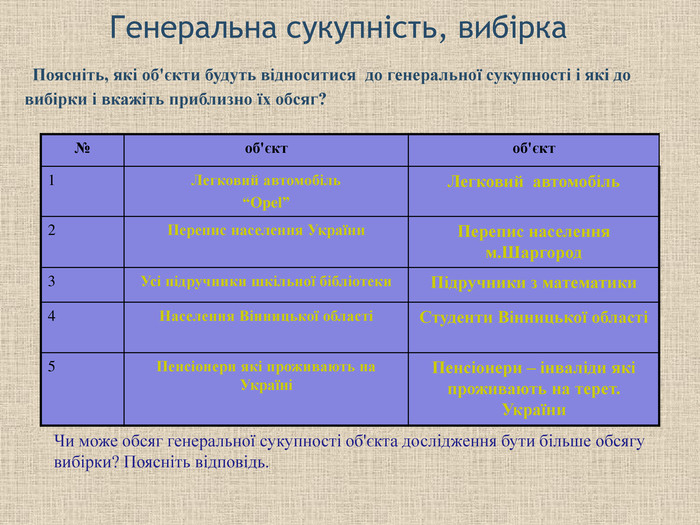
Генеральна сукупність, вибірка № об'єкт об'єкт 1 Легковий автомобіль “Opel” Легковий автомобіль 2 Перепис населення України Перепис населення м.Шаргород 3 Усі підручники шкільної бібліотеки Підручники з математики 4 Населення Вінницької області Студенти Вінницької області 5 Пенсіонери які проживають на Україні Пенсіонери – інваліди які проживають на терет. України Поясніть, які об'єкти будуть відноситися до генеральної сукупності і які до вибірки і вкажіть приблизно їх обсяг? Чи може обсяг генеральної сукупності об'єкта дослідження бути більше обсягу вибірки? Поясніть відповідь.

Завдання Поясніть, які пари об'єктів можна віднести до генеральної сукупності і вибірки, які ні? Поясніть свою відповідь. об'єкт об'єкт Зріст дорослих людей Зріст дітей Машини “КАМАЗ”в автопарку Машини вантажні Літнє взуття Зимове взуття Миші комп'ютерні Миші звичайні Зошити учнівські Зошити у клітинку одного учня

Якість вибірки  Зауваження Не треба вибирати дуже багато даних для дослідження – буде складно опрацьовувати отримані дані. Не треба обмежуватись вибіркою декількох сусідніх даних. Краще врахувати випадкові значення вибірки. Репрезентативність вибірки (якщо вона за своєю структурою максимально повторює структуру генеральної сукупності) Приклад Частина жінок і чоловіків серед населення міста складає відповідно 48% и 52%. Ці ж пропорції треба виконувати при вибірці дослідження. Якщо вони будуть порушені і на питання анкети відповіли 55% жінок и 45% чоловіків, то результати дослідження будуть мати суттєві помилки вибірки.

Приклад нерепрезентативної вибірки   У США одним з найбільш відомих історичних прикладів нерепрезентативної вибірки вважається випадок, що відбувся під час президентських виборів в 1936 року[1]. Журнал «Літрері Дайджест», що успішно прогнозував події декількох попередніх виборів, помилився в своїх прогнозах, розіславши десять мільйонів пробних бюлетенів своїм підписчикам, людям, вибраним по телефонним книгах всієї країни, і людям з реєстраційних списків автомобілів. У 25 % бюлетенів (майже 2,5 мільйона) голосів, що повернулися, були розподілені таким чином: 57 % віддавали перевагу кандидату-республіканцю Альфу Лендону 40 % вибрали діючого на той час президента-демократа Франкліна Рузвельта На дійсних же виборах, як відомо, переміг Рузвельт, набравши більше 60 % голосів. Помилка «Літрері Дайджест» полягала в наступному: бажаючи збільшити репрезентативність вибірки, — оскільки їм було відомо, що більшість їхніх передплатників вважають себе республіканцями, — вони розширили вибірку за рахунок людей, вибраних з телефонних книг і реєстраційних списків. Проте вони не врахували сучасних їм реалій і насправді набрали ще більше республіканців: у часи Великої депресії володіти телефонами і автомобілями могли собі дозволити переважно представники середнього і верхнього класу (в більшості республіканці, а не демократи). * *

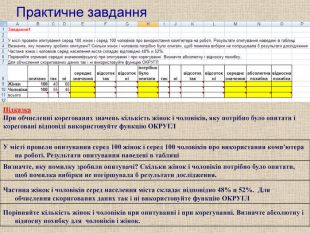
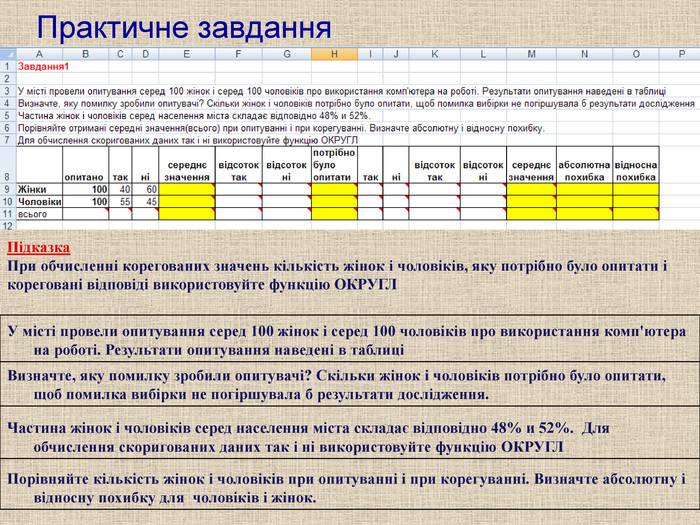
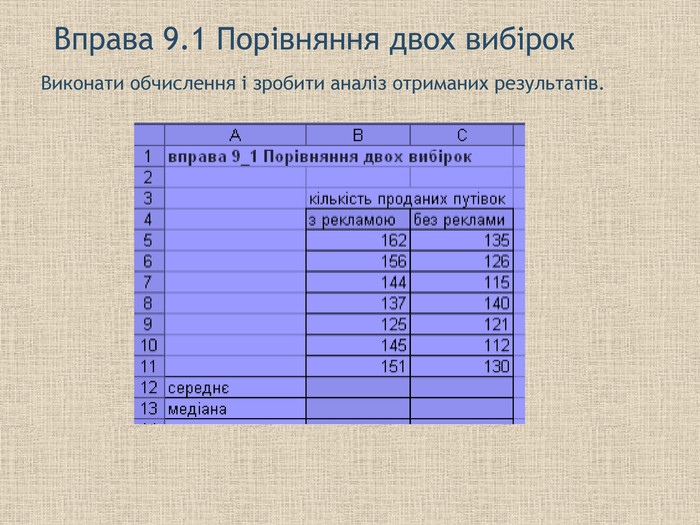
Практичне завдання У місті провели опитування серед 100 жінок і серед 100 чоловіків про використання комп'ютера на роботі. Результати опитування наведені в таблиці Визначте, яку помилку зробили опитувачі? Скільки жінок і чоловіків потрібно було опитати, щоб помилка вибірки не погіршувала б результати дослідження. Частина жінок і чоловіків серед населення міста складає відповідно 48% и 52%. Для обчислення скоригованих даних так і ні використовуйте функцію ОКРУГЛ Порівняйте кількість жінок і чоловіків при опитуванні і при корегуванні. Визначте абсолютну і відносну похибку для чоловіків і жінок. Підказка При обчисленні корегованих значень кількість жінок і чоловіків, яку потрібно було опитати і кореговані відповіді використовуйте функцію ОКРУГЛ

Узагальнення отриманих знань і результатів виконання завдання1 Дослідження якого об'єкту проводили? До якої галузі можна його віднести. Які статистичні дані збиралися? Вкажіть генеральну сукупність, вибірку, об'єм вибірки об'єкту дослідження. Як ви визначали відсоток опитаних, як це значення допомогло вам отримати скориговані значення по категоріям. Де ви тримали абсолютну і відносну похибки. Поясніть причину їх появи. Як запобігти появи цих похибок?

Урок 2 Бліц – опитування Етапи статистичного дослідження Розбір прикладів 1,2, завдання1. Статистичні показники вибірки Обчислення показників середнє арифметичне, мода, медіана. Виконання завдання 2

опитування Пояснити поняття і терміни Математична статистика це… Термін “статистика” ввів … Статистичні дані це… * 5. Генеральна сукупність це … 6. Вибірка це … 7. Варіанта це … 8. Поясніть, які пари об'єктів можна віднести до генеральної сукупності і вибірки, які ні? Поясніть чому. об'єкт об'єкт овочі фрукти відеокарта комп'ютер папка файл

Етапи статистичного дослідження Статистичне спостереження (Збір даних - процес, як правило, трудомісткий і дорогий. Як ви знаєте, цим займаються сьогодні цілі наукові інститути та фонди). Статистичні дані можна збирати не тільки прямими опитуваннями або вимірами, але і за допомогою сучасних засобів ІКТ з мережі Інтернет . Групування первинних статистичних даних (якщо досліджуються декілька ознак об'єкту) Аналіз статистичної інформації (обчислення середнього, найбільшого, найменшого, рангу, і т.д. і зробити висновки за триманими результатами). Приклад1 Нехай середня кількість дітей ясельного віку в місті оцінений вибірковим методом і склало 1,2 людини. Якщо в місті 1000 молодих сімей, то число необхідних місць в дитячих яслах отримують множенням цієї середньої на чисельність генеральної сукупності N = 1000, тобто складе 1200 місць. Приклад2 Дослідження якості запису і зберігання інформації на носіях. Які носії ви будете досліджувати? Як будете формувати вибірку? Як врахувати репрезентативність вибірки?

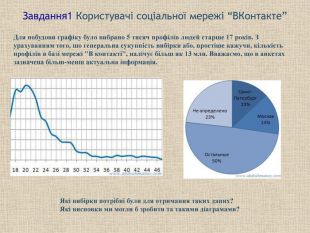
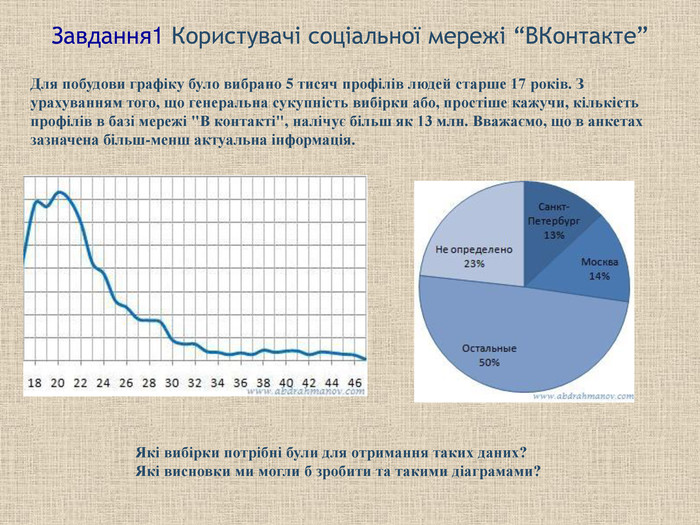
Завдання1 Користувачі соціальної мережі “ВКонтакте” Для побудови графіку було вибрано 5 тисяч профілів людей старше 17 років. З урахуванням того, що генеральна сукупність вибірки або, простіше кажучи, кількість профілів в базі мережі "В контакті", налічує більш як 13 млн. Вважаємо, що в анкетах зазначена більш-менш актуальна інформація. . Які вибірки потрібні були для отримання таких даних? Які висновки ми могли б зробити та такими діаграмами?

*

Мода (елемент вибірки, що зустрічається найчастіше) Середнє значення (середнє арифметичне) Медіана -таке значення, яке ділить упорядковану в порядку зростання або убування вибірку навпіл. Середнє квадратичне відхилення *

Середнє арифметичне Середнє арифметичне представляє собою таке значення ознаки, сума відхилень від якого вибіркових значень ознаки дорівнює нулю. де n - обсяг вибірки; xi - варіанти вибірки. Приклад 1 Протягом семи днів на міжвалютному банку долар коливався(7,44; 7,46; 7,46; 7,50; 7,54; 7,52;7,50). Тоді середнє арифметичне Хср= 7,44+ 7,46+7,46+ 7,50+ 7,54+ 7,52+7,50)/7=7,49 Приклад 2 Нехай у класі 18 учнів. З них 5 мають 9,6 середній бал, 3-10,2; 7-6,8; 3-8,4. Тоді середній бал класу Хср=(5*9,6+3*10,2+7*6,8+3*8,4)/18=8,4

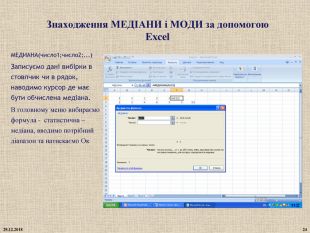
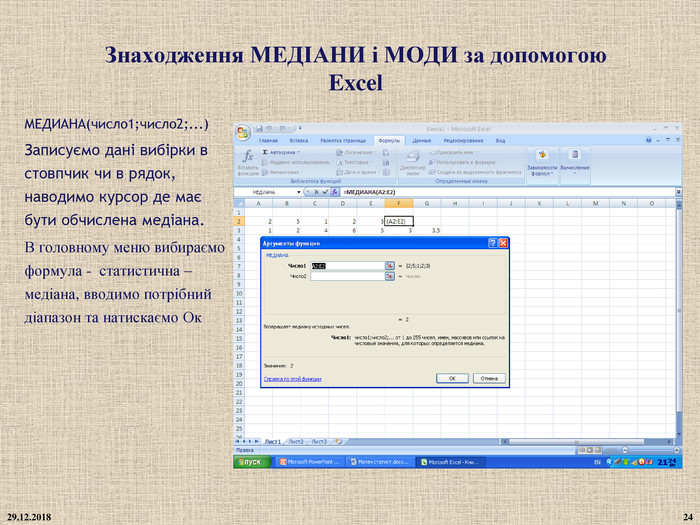
Медіана - Позначається буквою Mе. При непарній кількості випадкових величин за медіану приймається безпосередньо центральне значення. Якщо число значень у вибірці парне, то медіана виявляється між двома значеннями. У цьому випадку значення медіани розраховується як середнє арифметичне між ними. Приклад 1 N=5 , маємо зріст учнів класу (145, 160, 167, 156, 164) Упорядкуємо значення вибірки за зростанням. 145, 156, 160, 164, 167 Визначимо чи є об'єм вибірки непарним числом. N=5 – непарне. Ділимо об'єм вибірки навпіл і округлюємо тримане число у більшу сторону 5/2=2,5=3 Третя варіанта у вибірці =160 –це і буде медіана Ме=160см Приклад 2 N=6 , маємо ціну ноутбуків (3450, 4600, 6670, 5650, 6400, 4300) 1. Відсортована вибірка (3450, 4300, 4600, 5650, 6400, 6670) 2. N=6 – парне 3. Визначаємо сусідні варіанти 4600 і 5650. Знаходимо між ними середнє значення Ме=5125грн. Під час знаходження медіани дані повинні бути записані в порядку зростання(спадання)

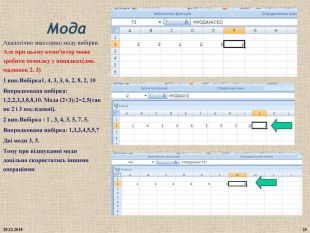
Мода це таке значення у вибірці, яке зустрічається найчастіше. Мо Приклад: 4, 2, 8, 8, 4, 8, 10. У даному випадку Мо= 8, тому що 8 зустрічається найчастіше у всій вибірці. 1 У випадку, коли всі значення вибірки зустрічаються однаково часто, то прийнято вважати, що вибірка не має моди. 4, 2, 6, 7, 5, 10 - не має моди. 2,2,4,5,4,5 - не має моди 2. Коли два сусідніх значення в упорядкованій вибірці зустрічаються однаково часто і частіше, ніж всі інші значення, то в цьому випадку мода дорівнює середньому значенню цих двох сусідніх величин. 1, 4, 3, 3, 6, 2, 8, 2, 10 1, 2, 2, 3, 3, 4, 6, 8, 10 - упорядкована вибірка. Мо = (2 +3): 2 = 2,5 1, 2, 2, 3, 5, 5, 7, 9 (2і 5 несуміжні то дві моди 2; 5)

Мода 3 ситуація. Якщо два не сусідніх значення в упорядкованій вибірці зустрічаються однаково часто і частіше, ніж всі інші значення, то в цьому випадку говорять, що вибірка має дві моди і називають вибірку бімодальною. Приклад: 4, 2, 3, 6, 4, 2 2, 2, 3, 4, 4, 6 Мо=2;4 Завдання : знайдіть моду вибірки 4,6,7,2,0,13,4,8,6,11

Знаходження МЕДІАНИ і МОДИ за допомогою Excel МЕДИАНА(число1;число2;...) Записуємо дані вибірки в стовпчик чи в рядок, наводимо курсор де має бути обчислена медіана. В головному меню вибираємо формула - статистична – медіана, вводимо потрібний діапазон та натискаємо Ок * *

Мода Аналогічно знаходимо моду вибірки. Але при цьому комп'ютер може зробити помилку у випадках(див. малюнок 2, 3) 1 вип.Вибірка1, 4, 3, 3, 6, 2, 8, 2, 10 Впорядкована вибірка: 1,2,2,3,3,8,8,10. Мода (2+3):2=2,5(так як 2 і 3 послідовні). 2 вип.Вибірка : 1 , 3, 4, 3, 5, 7, 5. Впорядкована вибірка: 1,3,3,4,5,5,7 Дві моди 3, 5. Тому при відшуканні моди доцільно скористатись іншими операціями * *

Статистична функція табличного процесора Ранг A Дані 7 3,5 3,5 1 2 Формула =РАНГ(A3;A3:A7;1) =РАНГ(A4;A3:A7;1) Функція ранг встановлює дані вибірки в порядку зростання. Далі зі впорядкованої вибірки самостійно вибираємо моду. Цю операцію доцільно здійснювати коли вибірка невелика. Ще моду можна здійснити за допомогою СЧЕТЕСЛИ Ранг числа - це його місце щодо інших значень у числовому списку. (Якщо список відсортувати, то ранг буде його позицією.) РАНГ (число; посилання; порядок)

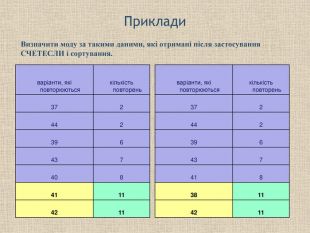
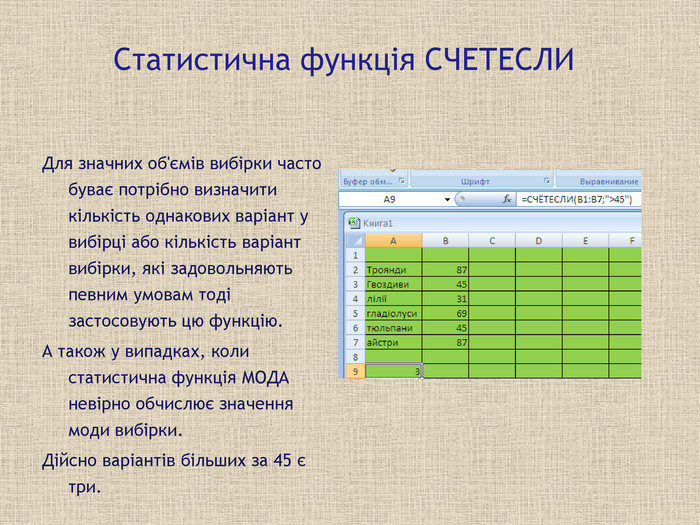
Статистична функція СЧЕТЕСЛИ Для значних об'ємів вибірки часто буває потрібно визначити кількість однакових варіант у вибірці або кількість варіант вибірки, які задовольняють певним умовам тоді застосовують цю функцію. А також у випадках, коли статистична функція МОДА невірно обчислює значення моди вибірки. Дійсно варіантів більших за 45 є три.

Складніші випадки Нехай нам задана якась вибірка (перша стрічка на малюнку).Бачимо усі можливі варіанти 2,3,4,6,7,9,13. За допомогою функції СЧЕТЕСЛИ шукаємо частість кожного варіанта (в таблиці правіше) .Далі скориставшись функцією рангу до діапозону І1:І7, отримаємо частість варіантів у порядку зростання. Клітинка у останньому рядку і першому стовпчику буде модою. * *

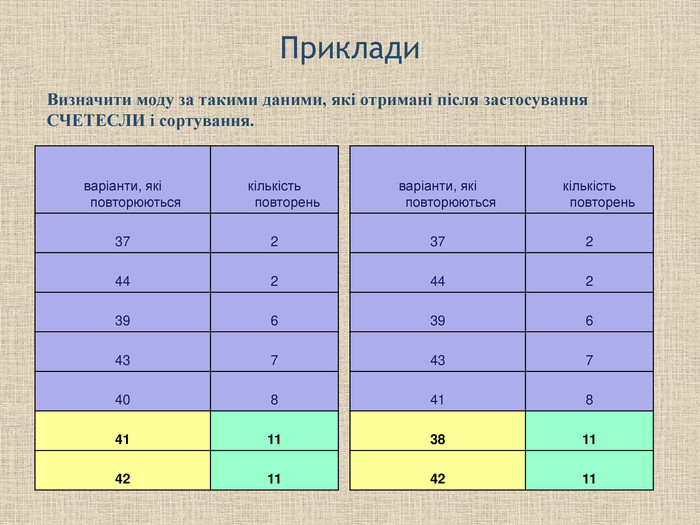
Обчислення моди у складних випадках засобами EXCEL Для використання функції СЧЕТЕСЛИ створіть нову додаткову таблицю і перенесіть в неї по одному значенню ті варіанти, які повторюються в першій таблиці. Підрахуйте скільки разів ці значення повторювалися серед варіант першої таблиці. Відсортуйте отримані значення у порядку зростання. Клітинка у останньому рядку і першому стовпчику буде модою. варіанти, які повторюються Кількість повторень 37 2 39 5 40 8 41 12 42 9 43 5 44 2 На аркуші Завдання2 спробуйте знайти значення моди описаним способом. =СЧЁТЕСЛИ($B$2:$B$45;D19) Варіанта 1 ст. таб.2 Вибірка у таб.1 варіанти, які повторюються кількість повторень 37 2 44 2 39 5 43 5 40 8 42 9 41 12 мода

Приклади варіанти, які повторюються кількість повторень 37 2 44 2 39 6 43 7 40 8 41 11 42 11 Визначити моду за такими даними, які отримані після застосування СЧЕТЕСЛИ і сортування. варіанти, які повторюються кількість повторень 37 2 44 2 39 6 43 7 41 8 38 11 42 11

Завдання 2 У результаті дослідження віку батьків десятикласників були отримані наступні статистичні дані. Обчислити середнє арифметичне, моду і медіану для цих не групованих статистичних даних. 39 41 40 42 41 40 42 44 40 43 42 41 43 39 42 41 42 39 41 37 43 41 37 43 42 41 40 41 38 44 40 39 41 40 42 40 41 42 40 43 39 41 41 42. Зауваження Спочатку упорядкуйте варіанти вибірки. Для обчислення моди у першому випадку можете використовувати функції РАНГ або СЧЕТЕСЛИ. РАНГ застосовуйте для невеликої кількості варіант. А СЧЕТЕСЛИ для значно більшої кількості варіант. середнє значення медіана мода без використання статистичних функцій з використанням статистичних функцій

Узагальнення отриманих знань і результатів виконання завдання2 Дослідження якого об'єкту проводили? До якої галузі можна його віднести. Які статистичні дані збиралися? Вкажіть генеральну сукупність, вибірку, об'єм вибірки об'єкту дослідження. Як ви визначали моду, медіану, середнє без застосувань статистичних функцій і з ними. Чи відрізняються ці результати? Які проблеми можуть виникнути при обчисленні моди в EXCEL і як їх подолати? Які висновки ми можемо зробити завдяки отриманим результатам?

Стандартне відхилення ступінь розкиду значень вибірки відносно середнього значення визначається за формулою: * * Середнє квадратичне відхилення показує, на скільки в середньому відхиляються варіанти від його середнього значення. Дисперсію можна обчислити за допомогою функції ДИСП, а звідти взявши квадратний корінь знаходиться квадратичне відхилення

Бліц – опитування Пояснити поняття і терміни Математична статистика це… Генеральна сукупність це … Вибірка це … Варіанта це … Вкажіть статистичні показники вибірки. Поясніть показники центру: середнє, медіана, мода. Обчисліть середнє, медіана, мода для наступної вибірки. * 1 3 5 4 2

Аналіз отриманих статистичних значень * 39 41 40 42 41 40 42 44 40 43 42 41 43 39 42 41 42 39 41 37 43 41 37 43 42 41 40 41 38 44 40 39 41 40 42 40 41 42 40 43 39 41 41 42. Отримані результати дають зробити припущення, що середній вік батьків старшокласників приблизно 41 рік, і що поява дітей у батьків вкладається у середньостатистичний вік (21-28 років). Це може свідчити про достатньо стабільну економічну ситуацію в країні, коли старшокласники були народжені.

Вправа 9.1 Порівняння двох вибірок Виконати обчислення і зробити аналіз отриманих результатів.

Узагальнення отриманих знань і результатів виконання практичної роботи Дослідження якого об'єкту проводили? До якої галузі можна його віднести. Які статистичні дані збиралися? Вкажіть генеральну сукупність, вибірку, об'єм вибірки об'єкту дослідження. Як ви визначали моду, медіану, середнє без застосувань статистичних функцій і з ними. Чи відрізняються ці результати? Які проблеми можуть виникнути при обчисленні моди в EXCEL і як їх подолати? Які висновки ми можемо зробити завдяки отриманим результатам?