Презентація "Суміжні кути"

Геометрія 7 клас Суміжні кути

Вправа на розвиток уваги та пам’яті

Актуалізація опорних знань

План вивчення Аксіоми, означення, теореми. Означення суміжних кутів. 1 2 3 Теорема про суміжні кути. 4 Наслідки з теореми про суміжні кути.

Аксіоми в геометрії — це твердження про основні властивості найпростіших геометричних фігур, прийняті як вихідні положення. У перекладі з грецької слово «аксіома» означає «прийняте положення». Аксіоми

Твердження, у якому пояснюється зміст того чи іншого поняття, називають означенням. Означення вказує на особливості описаної фігури. Нам уже відомі деякі означення — відрізка, кута, середини відрізка. Означення

Теорема — це математичне твердження, справедливість якого встановлюється за допомогою міркувань. Такі міркування називають доведенням теореми. На основі аксіом за допомогою логічних міркувань ми отримуємо нові геометричні факти. Для доведення теорем використовують означення, аксіоми, доведені раніше теореми. Кожна теорема містить умову (що дано) і висновок (що необхідно довести). Твердження, які випливають безпосередньо з аксіом чи теорем, називають наслідками. Теорема

Суміжні кути Два кути називають суміжними, якщо одна сторона в них спільна, а дві інші сторони є доповняльними променями.

Теорема про суміжні кути

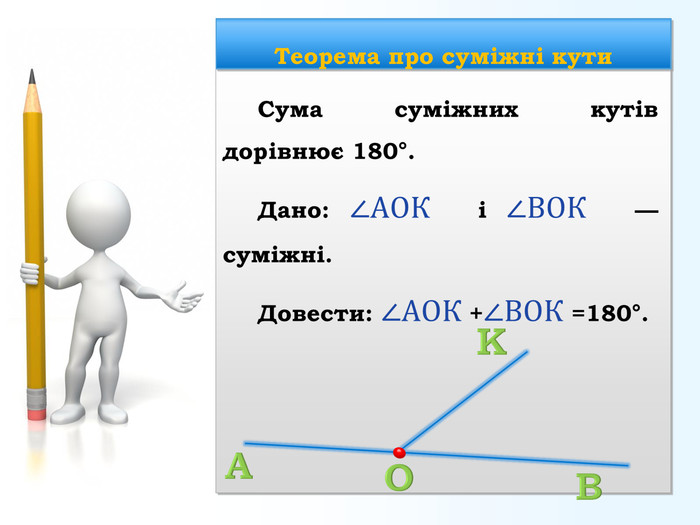
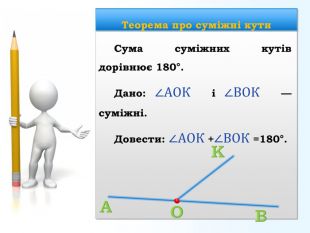
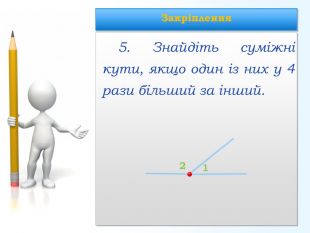
Доведення Кути AOK і BOK суміжні за умовою, тоді промені OA і OB — доповняльні (за означенням суміжних кутів), і кут AOB розгорнутий (за означенням розгорнутого кута), тобто ∠АОВ =180°. Оскільки промінь OK проходить між сторонами кута AOB (за означенням), то ∠АОК +∠ВОК =∠АОВ , отже, ∠АОК +∠ВОК =180° (за аксіомою вимірювання), що й треба було довести.

Наслідки

Наслідок 2. Кут, суміжний із прямим кутом,— прямий. Доведення Нехай ∠АОВ =90°. Оскільки сума суміжних кутів дорівнює 180°, то градусна міра другого суміжного кута ∠ВОС дорівнює: 180°-90°=90°, що й треба було довести. Наслідки

Наслідки

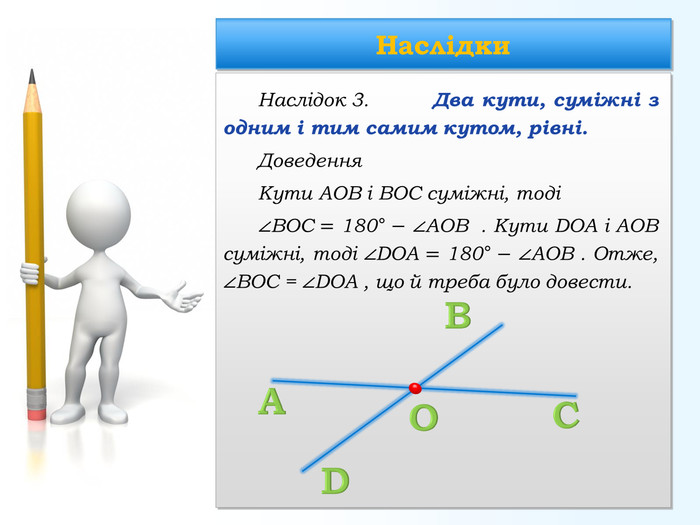
Наслідок 4. Кут, суміжний із гострим кутом,— тупий; кут, суміжний із тупим кутом, — гострий. Це випливає з теореми про суміжні кути, оскільки, якщо два нерівні кути у сумі становлять 180°, то один з них більший за 90°, тобто тупий, а інший — менший від 90°, тобто гострий, що й треба було довести. Наслідки

Закріплення

1. Сума двох кутів дорівнює 170°. Чи є вони суміжними? Відповідь обґрунтуйте. Закріплення

2. Чи є правильним твердження: «Якщо сума двох кутів дорівнює 180°, то вони суміжні»? Відповідь обґрунтуйте. Закріплення

3. Знайдіть кут, суміжний із кутом 75°. Закріплення

Розв’язання

4. Знайдіть суміжні кути, якщо один із них на 28° менший від іншого. Закріплення

Розв’язання

5. Знайдіть суміжні кути, якщо один із них у 4 рази більший за інший. Закріплення

Розв’язання

Закріплення №98 №86

Логічна вправа

АНАГРАМИ КУТ НАПРЯМ ЕІКЛІД ГЕОМЕТРІЯ

Рефлексія

Домашнє завдання Опрацювати §4; 5 Розв’язати: № 87; № 95 Додатково: № 101*