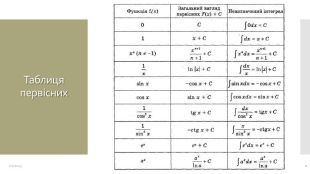
Презентація "Таблиця первісних. Правила знаходження первісних"
Про матеріал
Застосування таблиці первісних для розв'язування вправ та підготовки до ЗНО Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку