Розробка уроку з алгебри "Квадрат суми та різниці двох виразів"

Крят В.М. ,

учитель математики, учитель-методист

Опорний заклад «Хорольська гімназія Хорольської міської  ради Лубенського району Полтавської області»

kriatvn@gmail.com

КВАДРАТ СУМИ ТА РІЗНИЦІ ДВОХ ВИРАЗІВ

Урок, 7 клас

Використовується підручник: Кравчук В.Р.,Підручна М.В.Янченко Г.М.,Алгебра:Підручник для 7 класу загальноосвітніх навчальних закладів – Тернопіль; видавництво «Підручники і посібники», 2015.

Тема. Квадрат суми та різниці двох виразів.

Тип уроку. Урок засвоєння нових знань і формування початкових умінь.

Мета уроку: організувати діяльності учнів для самостійного виведення формул квадрата суми і квадрата різниці двох виразів, домогтися засвоєння цих формул, сформувати вміння використовувати їх для розв’язування вправ. Розвивати творче мислення,обчислювальні навички, інтересу до математики. Виховати культуру спілкування та комунікативні навички.

Очікувані результати: Учні повинні знати формули квадрата суми і квадрата різниці двох виразів, вміти використовувати їх для розв’язування вправ.

Обладнання: інтерактивні засоби навчання, роздатковий матеріал.

Хід уроку.

I. Підготовчий етап.

За кілька днів до проведення уроку учні класу об’єднуються в п’ять різнорівневих груп. Учитель конкретизує завдання кожної групи, надає вказівки щодо організації їх роботи, пропонує додатковий матеріал та літературу.

ІІ. Організаційний момент.

Вступне слово вчителя. Ви вже навчилися виконувати множення раціональних виразів. Іноді це громіздкі і складні алгебраїчні перетворення, які часто хотілося б виконати простіше. Виявляється це можливо. Сьогодні на уроці ми познайомимося із двома дуже важливими формулами, які дадуть можливість раціонально перетворювати алгебраїчні вирази. Їх називають формулами скороченого множення. Спочатку попрацюємо усно, розпочавши з традиційної п’ятихвилинки.

ІII. Актуалізація опорних знань.

Учням пропонується розв’язати завдання на повторення матеріалу, які проектуються на дошку.

Усні вправи

1.Піднести до квадрата вираз: а) 3а; б) -5; в) 0,2с;г) .

2. Знайти подвоєний добуток двох виразів:

а) 2 та 1;   б) х та 3;    в) 4 та у    г) 5та 2а.

3. Прочитати вираз:

а) а ² + в²

б) (х-у)(х+у)

в) х ² – у²

г) (а+в)²

д) (а-в)²      

Вчитель звертає увагу учнів на два останні вирази. Як ще по іншому їх можна записати? Чи можна їх представити у вигляді многочлена і як це робити найраціональніше? Протягом уроку ми будемо шукати відповіді на ці запитання.

ІV. Формування нових навичок.

Здавна було помічено, що множення деяких многочленів можна виконати швидше. Формули, які дають можливість це робити називають формулами скороченого множення. Зараз ви навчитеся виводити формули квадрата суми і квадрата різниці двох виразів, які відносяться до формул скороченого множення і застосовувати їх для  перетворення квадрата двочлена в тричлен виду a²± 2ab + b.² Оголошується тема уроку ” Квадрат суми і квадрат різниці двох виразів.

Всі учні виконують вправи самостійно в зошитах (при необхідності можливе спілкуванні в групах), в той час, як два учні працюють над ними, на дошці.

Письмові вправи

Виконайте множення двочленів.

             1 варіант:                                 2 варіант:  

           1). (а+в)(а+в)                                1). (х+у)(х+у)

           2). (с+d)(c+d)                                 2). (m+n)(m+n)

           3). (x+3)(x+3)                                 3). (a+2)(a+2)

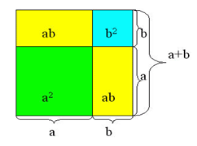
 Після чого, під керівництвом вчителя, проводиться фронтальне обговорення результатів. Отримані результати, пропонується записати у вигляді, (а+в)(а+в)=(а+в) ² = а² + 2ав + в² ,що дає змогу учням самостійно зробити висновок про те, як швидко піднести суму двох виразів до квадрату. Записується формула (а+в) ² = а² + 2ав + в²   і формулюється правило.

Квадрат суми двох виразів дорівнює квадрату першого виразу, плюс подвоєний добуток першого и другого виразів, плюс квадрат другого виразу.

Над виконанням наступної вправи учні працюють самостійно в групах.

Письмові вправи

Виконайте множення двочленів.

1. (а-в)(а-в)                               4. (х-у)(х-у)
2. (с-d)(c-d)                               5. (m-n)(m-n)
3. (х-3)(х-3)                              6. (а-2)(а-2)

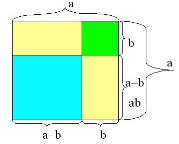
Проаналізувавши отримані рівності виду . (а-в)(а-в)= (а-в)² = а² – 2ав + в,² записується висновок у вигляді формули (а-в)² = а² – 2ав + в² та формулюється правило, як піднести до квадрата різницю двох виразів.          

Квадрат різниці двох виразів дорівнює квадрату першого виразу, мінус подвоєний добуток  першого и другого виразів, плюс квадрат другого виразу.

Учитель наголошує, що ,надалі,отримані формули будуть постійно використовуватися для піднесення двочлена до квадрату. Це дасть можливість раціонально і швидко отримати результат.

Геометрична інтерпретація.

Вчитель зауважує, що, оскільки, алгебра тісно пов’язана з геометрією, то виведені формули мають геометричний зміст. Античні математики використовували формули скороченого множення задовго до нашої ери. На той час формули подавалися не у звичному нам символічному вигляді, а формулювалися словами. Формули квадрата суми і різниці двох виразів знали ще давньогрецькі математики, але буквенну символіку вперше застосував у своїх працях Діофант Александрійський, який жив у ІІІ столітті. Учені Давньої Греції алгебраїчні твердження, формули, що виражають певні залежності між величинами, трактували геометрично і доводили тільки для додатних чисел. Замість додавання чисел говорили про додавання відрізків, під добутком двох чисел розуміли площу прямокутника.

Самостійна робота в групах.

Учням пропонується виконати геометричну інтерпретацію алгебраїчного твердження, яке було відоме давньогрецьким ученим і яке в геометричній термінології формулювали так: площа квадрата, побудованого на сумі двох відрізків, дорівнює сумі площ квадратів, побудованих на кожному з цих відрізків, плюс подвоєна площа прямокутника, побудованого на цих відрізках. Доведення презентуватиме представник групи, яка першою отримає результат.

Практичне завдання.

Із різнокольорових геометричних фігур (прямокутників і квадратів) скласти геометричну ілюстрацію доведень формул квадрата суми і квадрата різниці.

Переконатися в правильності геометричної інтерпретації отриманих формул пропонується за готовими рисунками, які проектуються на екран.

V. Закріплення вмінь і навичок.

Закріплення матеріалу проводиться шляхом розв’язування вправ.

Усні вправи

1. Виберіть правильну відповідь до виразів.

1.                (8+а)²                            3. х ² – 2хm + m²
2.                (2-х)²                             1. 64 – 16 а + а ²
3.                (х-m)²                            4.  п ² + 2вп + в²
4.                (п+в)²                            2.  4- 4х + х ²    

2. Знайдіть допущені помилки.

(а-в)²=а²-2ав+в

(а-в)²=а²-  ав+в²

(а-в)²=а²+2ав-в²

(а-в)²=а²-2ав-в²

(а+в)²=а+2ав+в²

(а+в)²=а²+2ав-в²

(а+в)²=а²-2ав-в²

Письмові вправи

Коментоване виконання вправ №456, №459 №464 учнями на дошці, яке завершується проведенням гри «Математична естафета».

Гра «Математична естафета».

У кожної групи на столах карточки, які містять правильну відповідь до. завдань, запропонованих на дошці. Учень,який знайшов правильну відповідь першим, прикріпляє відповідну карточку на дошку магнітом.

1.  (а-2)²                               16-8в+в²
2. (х+у)²                              25+10с+с²
3. (4-в)²                               а²-4а+4
4. (m+3)²                             1-2а+а²
5. (5+с)²                               х²+2ху+у²
6. (2+х)²                              3в+12в+в²
7. (1-а)²                                m²+6m+9
8. (6+в)²                               m²-2my+y²
9. (n+a)²                               4+4x+x² 
10. (m-y)²                               n²+2an+a²  
11. (c-d)²                                c²-2cd+d²
12. (2x-1)²                             25x²+20x+4
13. (4+3y)²                            36-24a+4a²
14. (5x+2)²                            4x²-4x+1
15. (6-2a)²                             16+24y+9y²

VІ. Підсумок уроку.

VІІ. Домашнє завдання.Із підручника вивчіть § 4. П. 13 № 457, №459, № 461.

Список літератури:

1. Абрамчук В.С.та ін. Посібник шкільного курсу з математики. – К.: Техніка, 2008. – 736 с.

2. Маланюк М.П., Лукавецький В.І. Олімпіади юних математиків. – К.: Радянська школа., 1977. – 102с.

3. Сікорський К.П. Додаткові розділи з курсу математики 7-8 класів для факультативних занять. – М.: Просвіта, 1969. – 320с

4. Ушаков Р.П. та ін. Повторювальний курс з математики. – К.: Техніка, 2003. – 590 с.