Презентація. Тема "Тригонометричні рівняння".
Про матеріал
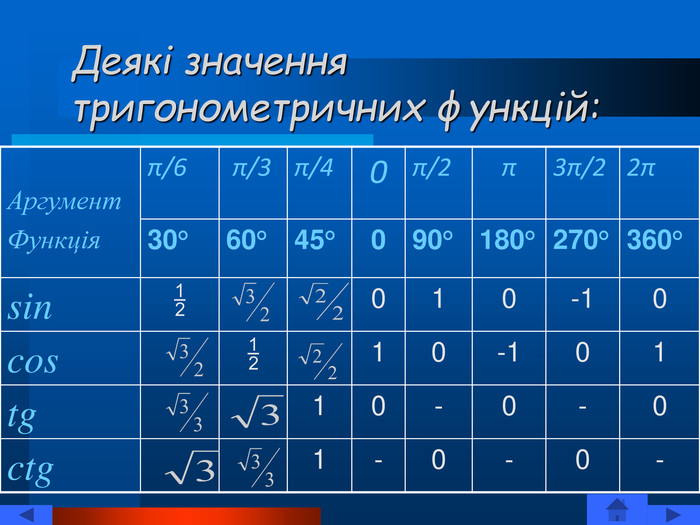
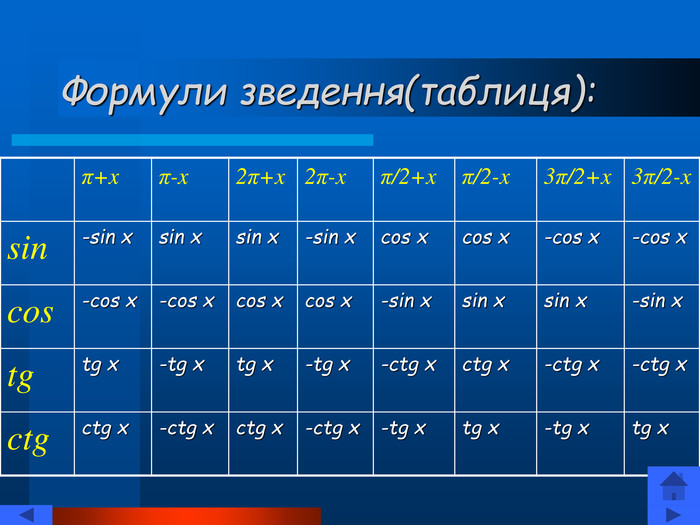
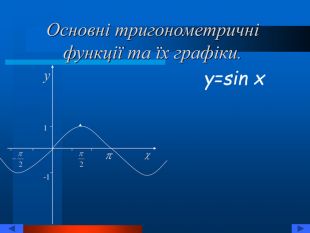
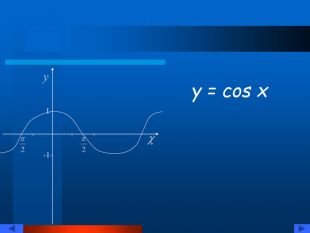
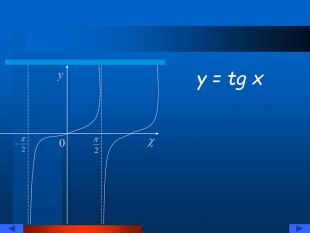
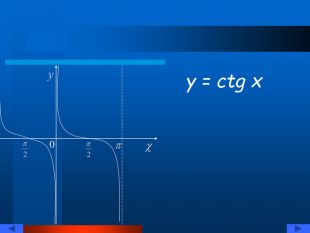
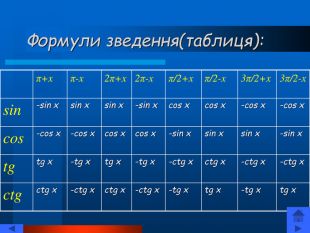
Презентація "Тригонометричні рівняння" познайомить вас із тригонометричними функціями, їх графіками та властивостями. Тут ви зможете знайти різноманітні формули: основні тригонометричні тотожності, формули зведення, формули перетворення суми тригонометричних функцій в добуток і навпаки, формули половинного, подвійного, потрійного кута. Ви познайомитесь із розв'язуванням різних типів рівнянь. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра і початки аналізу (профільний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
До уроку
§ 5. Тригонометричні рівняння і нерівності Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


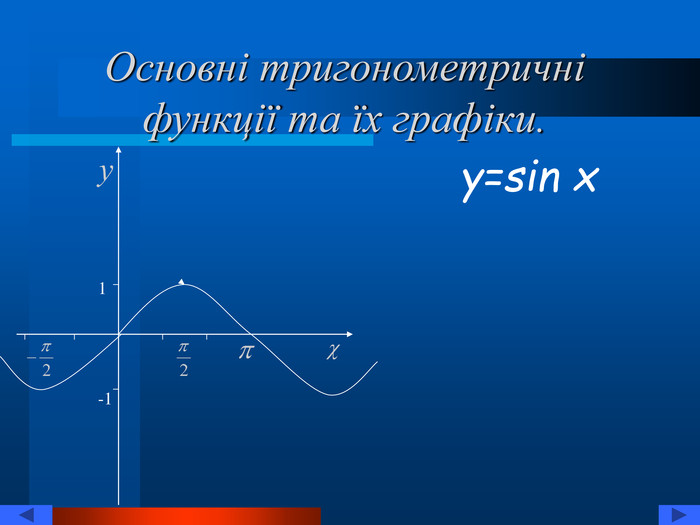
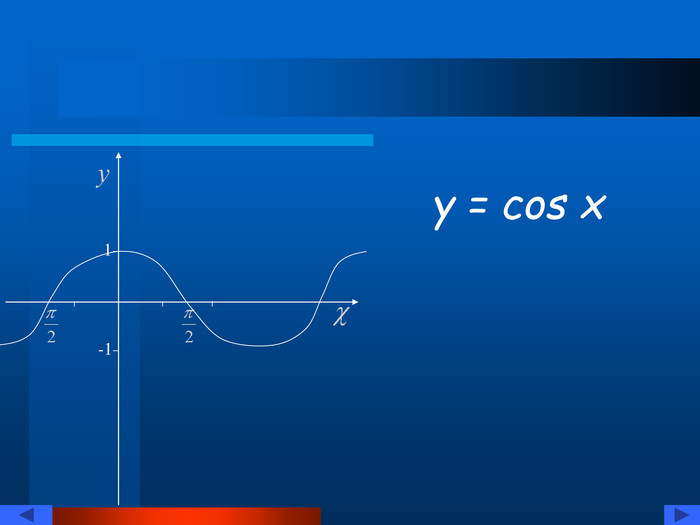
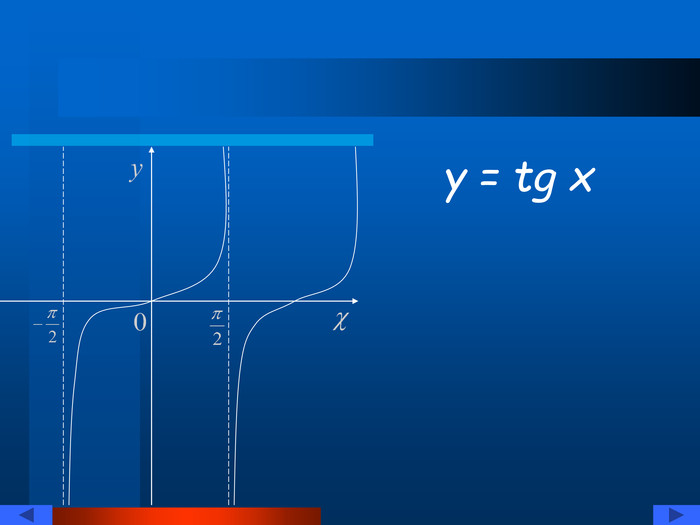
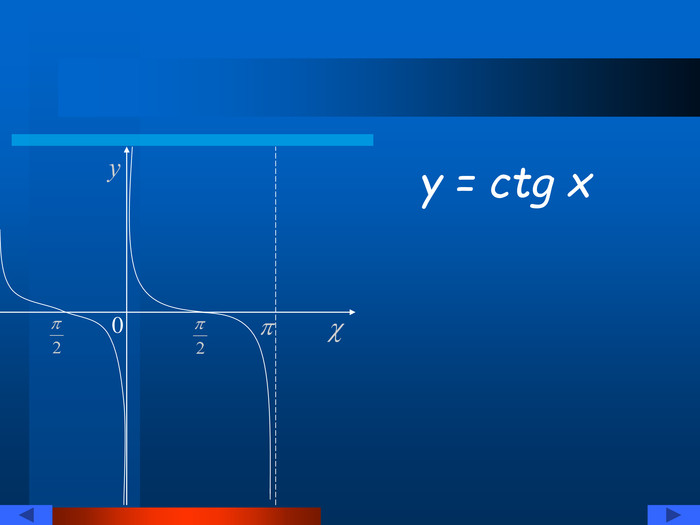
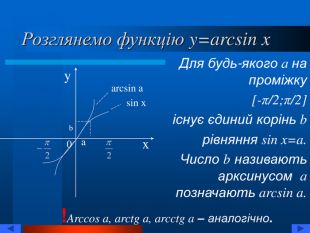
![Розглянемо функцію y=arcsin x !Arccos a, arctg a, arcctg a – аналогічно. Для будь-якого а на проміжку [-π/2;π/2] існує єдиний корінь b рівняння sin x=a. Число b називають арксинусом а позначають arcsin a. y 0 x a b arcsin a sin x Розглянемо функцію y=arcsin x !Arccos a, arctg a, arcctg a – аналогічно. Для будь-якого а на проміжку [-π/2;π/2] існує єдиний корінь b рівняння sin x=a. Число b називають арксинусом а позначають arcsin a. y 0 x a b arcsin a sin x](/uploads/files/733390/152361/164966_images/6.jpg)