Урок у 8 класі " Теорема Піфагора"

Теорема Піфагора. Розв’язання задач.

Мета:

систематизувати та узагальнити знання учнів з теми, установити правильність усвідомлення вивченого теоретичного матеріалу, виявити прогалини первинного осмислення матеріалу, неправильні уявлення учнів;

формувати обчислювальні навички учнів, розвивати розумові здібності учнів, їх інтелектуальні якості: здатність до бачення проблеми, самостійність, гнучкість, діалектичність мислення, вчити об’єктивно оцінювати себе і коригувати свою діяльність в ході уроку,;

виховувати інтерес до процесу навчання, відповідальність за свідоме засвоєння знань.

Тип уроку. Урок засвоєння навичок і вмінь.

Наочність та обладнання: Вчительська презентація до уроку, портрет Піфагора, підручник, тестові завдання на компютере, математичне лото.

Хід урока

1. Організаційний етап.

Налаштування на гарний настрій на уроці.

Невідомо хто, коли, але хтось сказав слова, які передаються нам і які передаємо ми своїм нащадкам: «Намагайтеся кожного дня для кожної справи знайти якийсь позитивний початок, оскільки від того настрою, з яким ви вступаєте в день, або в справу, залежать ваші успіхи, а можливо і невдачі». Я бажаю вам розпочати урок з гарним настроєм і отримати від нього задоволення і гарні результати.

2. Формулювання мети й завдань уроку.

Щодня в своєму житті кожна людина стикається з багатьма завданнями, які неможливо виконати без знання математики, тобто без розв’язування різноманітних задач. Але для цього треба знати теоретичний матеріал.

І, оскільки тема сьогоднішнього урока «Теорема Піфагора. Розвязання задач.» Девізом його є слова: «Не досить оволодіти премудрістю, потрібно також вміти користуватись нею». (Слайд 1,2)

Сьогодні на уроці ми дізнаємось наскільки добре ви засвоїли її, і хто з вас зможе подолати «віслючий міст».

3. Мотивація навчальної діяльності.

Якщо відомості про «віслючий міст» не знайшли учні самостійно, то їх повідомляє вчитель:

В давнину теорему Піфагора називали «віслючий міст». Це тому, що учнів, які завчили теорему напам’ять, але не розуміли її, називали віслюками, для них вона була ніби непрохідним мостом. Бажаю вам всім перейти цей міст. (слайд 3)

4. Актуалізація опорних знань, умінь та навичок учнів.

 «Геометричний хокей».

На екрані з’являються запитання. Першого учасника вибирає вчитель. Якщо він правильно відповідає на запитання, то шайба вважається забитою в ворота вчителя, якщо ні – в ворота учнів. Далі учні «пасують» запитання один одному «Незакінчене речення». (слайд 4)

•   Який трикутник називається прямокутним...
•   Сума гострих кутів прямокутного трикутника дорівнює...
•   Сторона, що лежить напроти прямого кута, називається...
•   Сторони, що прилягають до прямого кута в прямокутному трикутнику, називається...
•   Як називається найдовша сторона прямокутного трикутника...
•   В прямокутному трикутнику квадрат гіпотенузи дорівнює...
•   Катет дорівнює ...
•   У прямокутному трикутнику будь-який катет менше...

5. Закріплення і корекція знань, умінь та навичок учнів.

Усні вправи

а) Обчисліть:

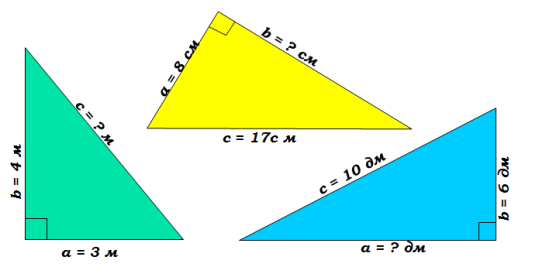б) Розв’язання задач за готовими малюнками (слайд 6)

в) «Мозковий штурм». Знайти Х. (слайд 7-8)

г) Колективне розв’язання задач

Ці задачі не прості,

Застосуєш їх в житті.

Щоб їх добре розв’язати,

Геометрію треба знати.

№1. Між двома електричними стовпами відстань між якими дорівнює15м, відбувся обрив дроту. Знайдіть скільки потрібно метрів дроту замінити, якщо висота стовпів 12м і 4м.

№2. В розрізі теплиця має рівнобедрений трикутник з бічними сторонами по 13м і основою 24м. Знайти висоту теплиці.

д) Вправа «Оціни себе» (слайд11)

Самосмійна робота

•          Середній рівень – математичне лото. (Додаток)
•          Достатній і високий рівень – тести на комп’ютері. (Додаток)

5. Історічна довідка.

Єгипетський трикутник

Ще в давньому Єгипті була відома теорема, яка потім отримала назву «Теорема Піфагора». Вона застосовувалась тоді для побудови прямих кутів на місцевості за допомогою мотузки з вузликами, яку натягували в вигляді трикутника зі сторонами 3, 4 і 5 вузлів. Звідси і походить назва давніх землемірів – «гарпедонапти» - натягувачі мотузок. А трикутник, сторони якого відносяться як 3:4:5,  назвали єгипетським. 

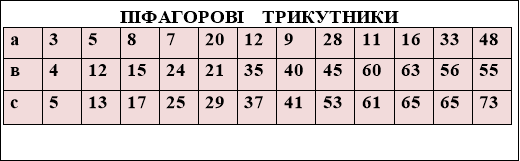
Піфагоровими трикутниками називають прямокутні трикутники, довжини сторін яких виражаються теж натуральними числами.

6. Домашнє завдання

Знайдіть декілька піфагорових трикутників (крім тих, сторони яких кратні сторонам єгипетського трикутника).

7. Підсумки уроку. Рефлексія.

•        Чи впорались ми з завданням?
•        Чи всі подолали «віслючий міст»?
•        Які риси характеру допомагали вам у цьому?
•        Які заважали?