Урок "Перпендикуляр і похила"
ГЕОМЕТРІЯ Клас 8
Дата ______
Тема. Перпендикуляр і похила.
Мета: домогтися засвоєння учнями поняття похилої та її проекції; довести властивості похилих, проведених з однієї точки до прямої, і їх проекцій; формувати вміння і навички застосовувати набуті знання до розв'язування задач; розвивати творчу ініціативу та розумові здібності учнів, самостійність, культуру спілкування, математичне мовлення, вміння міркувати, порівнювати, робити висновки, узагальнювати; виховувати почуття колективізму, відповідальності, наполегливість у досягненні мети, віру у свої сили, інтерес до математики.
Тип уроку: засвоєння нових знань.
Обладнання: презентація, картки з малюнками для усного рахунку.
Епіграф до уроку:
Єдиний шляx, що веде до
знань – діяльність.
Б.Шоу
Хід уроку
I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ.
- № 575.
-
 Розв'язування задач за готовими рисунками
Розв'язування задач за готовими рисунками
![]()
![]()
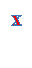
![]() Метод «Мозковий штурм». Знайдіть х.
Метод «Мозковий штурм». Знайдіть х.

![]()

 N
N
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() P D
P D
ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
Розминка. Інтерактивна технологія «Мікрофон»
1. Який трикутник називають прямокутним?
2. Чому дорівнює сума гострих кутів прямокутного трикутника?
3. Як називають найдовшу сторону прямокутного трикутника?
4. Чи може в прямокутному трикутнику бути два прямих кути?
5. Чи може в прямокутному трикутнику бути два рівних катети?
6. Чому дорівнюють кути такого трикутника?
7. Якщо сторони трикутника дорівнюють 6 см, 8 см, 10 см, то кут, протилежний стороні 10 см, дорівнює... (90°).
8. Сформулюйте теорему Піфагора.
9. Якщо в прямокутному трикутнику катет, протилежний куту 45°, дорівнює 7 см, то другий катет дорівнює... (7 см).
10. Якщо гіпотенуза прямокутного трикутника дорівнює 8 см, то катет, прилеглий до кута 60°, дорівнює... (4 см).
III. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ. ПОВІДОМЛЕННЯ ТЕМИ, МЕТИ, ЗАВДАНЬ УРОКУ
Учитель. Щоб розв'язати задачі за готовими рисунками, ми застосовували теорему Піфагора — одну з головних теорем у геометрії.
Із неї чи з її допомогою можна довести більшість теорем, властивостей і розв'язати багато задач. Про важливість теореми Піфагора говорить такий цікавий факт:
в 1974 році до сузір'я Геркулес із Землі було відправлено потужний радіосигнал, який містив у собі 1679 найважливіших повідомлень і відкриттів. Це була закодована в малюнку інформація про числа, хімічні елементи, геном людини, Сонячну систему . Серед них було зашифровано і теорему Піфагора.
Але дізнатись про те, чи змогли інші істоти зрозуміти цю теорему, людство зможе тільки через 50 тисяч років. Саме через цей час сигнал повернеться на Землю.
IV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ.
Проведемо геометричний експерименти.
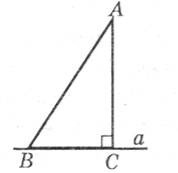
Накресліть у зошиті пряму а. Позначте точку А, що не лежить на даній прямій. З точки А проведіть перпендикуляр АС до цієї прямої. По обидва боки від перпендикуляра проведіть дві рівні похилі АВ і АО та похилу АЕ, що не дорівнює даним.
![]()


 А
А
![]()
![]() а
а
В С О Е
Зробіть необхідні вимірювання і сформулюйте висновки.
- Порівняйте довжину перпендикуляра з довжиною кожної похилої.
- Які співвідношення існують між похилими різної довжини, проведеними з однієї точки до прямої, і їх проекціями?
- Що можна сказати про співвідношення між рівними похилими, проведеними з однієї точки до прямої, і їх проекціями?
Доведення тверджень
- Доведіть, що якщо до прямої з однієї точки проведено перпендикуляр і похилу, то будь-яка похила більша за перпендикуляр.
|
|
Доведення
У прямокутному трикутнику АВС ( |
- Доведіть, що з двох похилих, проведених з однієї точки до прямої, більшою є та, проекція якої більша, і навпаки.
|
|
Доведення
Із прямокутних трикутників АВС ( |
- Рівні похилі, проведені з однієї точки до прямої, мають рівні проекції, і навпаки. Консультант групи організовує роботу всіх членів групи так, щоб кожний самостійно виконав певну частину роботи.
|
|
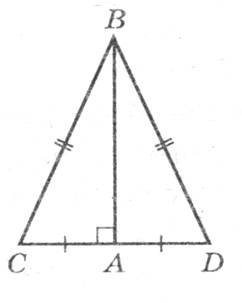
Доведення І спосіб. ΔСАВ=ΔDAB за гіпотенузою і катетом (ВА – спільний катет і ВС=BD), тому АС=AD. ІІ спосіб. ΔCBD – рівнобедрений (ВС=BD). Отже, АВ – висота й медіана ΔСВD, тому АС=AD. ІІІ спосіб. ВС=ВD, тобто точка В рівновіддалена від кінців відрізка CD, отже, вона лежить на серединному перпендикулярі до відрізка CD, тоді АС=АD.
IV спосіб. Із прямокутних трикутників САВ ( АС2=ВС2-АВ2, AD2=BD2-AB2. Оскільки ВС=ВD, то АС2=АD2, АС=АD. Міркуючи аналогічно у зворотному порядку, можна довести обернене твердження: з того, що АС=AD випливає, що ВС=ВD. |
V. ЗАКРІПЛЕННЯ НОВИХ ЗНАНЬ
Розв'язування задач
Задача 1 (усно). З однієї точки до прямої проведено дві рівні похилі. Відстань між їх основами становить 12 см. Визначте проекції похилих на дану пряму.
Відповідь. 6 см, 6 см.
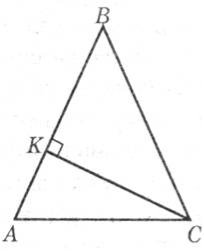
Задача 2. Бічна сторона рівнобедреного трикутника більша за основу і дорівнює 13 см, а проведена до неї висота — 5 см. Знайдіть довжину більшого з відрізків, на які висота ділить бічну сторону трикутника.
|
|
Розв’язання Нехай ΔАВС –даний рівнобедрений трикутник, у якому АВ=ВС=13 см. Оскільки СК – висота, проведена до бічної сторони, а BC>AC, то BK>AK, тобто ВК – більший з відрізків, на які висота ділить бічну сторону трикутника.
Із прямокутного ΔВКС (
Відповідь. 12 см. |
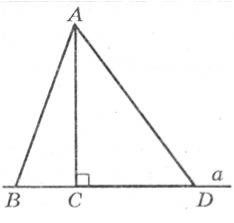
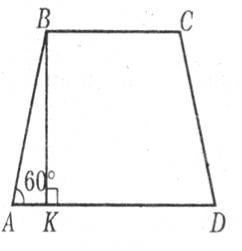
Задача. Основи рівнобічної трапеції дорівнюють 7 см і 15 см, гострий кут — 60°. Знайдіть периметр трапеції.
|
|
Розв’язання
Нехай АВСD – подана рівнобічна трапеція (ВС||AD), у якої ВС=7 см, AD=15 см, Проведемо висоту ВК.
У прямокутному трикутнику АКВ (
як катет, що лежить проти кута 30°. АВ=8 см. Р=2АВ+ВС+AD, Р=16+7+15=38 (см). Відповідь. 38 см. |
VІ. ПІДСУМОК УРОКУ
Метод «Знайди помилку»
1. Якщо з однієї точки до прямої проведено дві похилі, то менша похила має більшу проекцію.
2. Проекція похилої коротша від самої похилої.
3. Похила коротша за перпендикуляр, проведений з тієї самої точки на ту саму пряму.
4. Якщо в трикутнику квадрат однієї його сторони дорівнює сумі квадратів двох інших, то кут напроти найбільшої сторони — гострий.
5. Квадрат катета прямокутного трикутника дорівнює різниці квадратів гіпотенузи та іншого катета.
VII. ДОМАШНЄ ЗАВДАННЯ
Вивчити § 14, повторити § 13.
Розв'язати № 634.


про публікацію авторської розробки
Додати розробку