Презентація "Теорема Піфагора"
Про матеріал
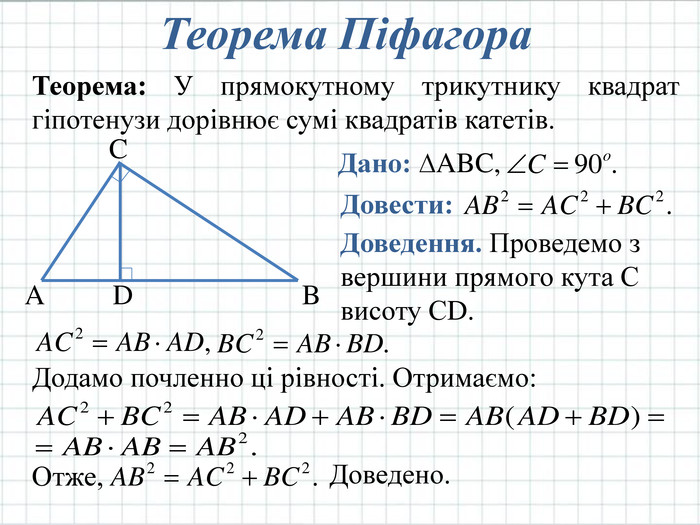
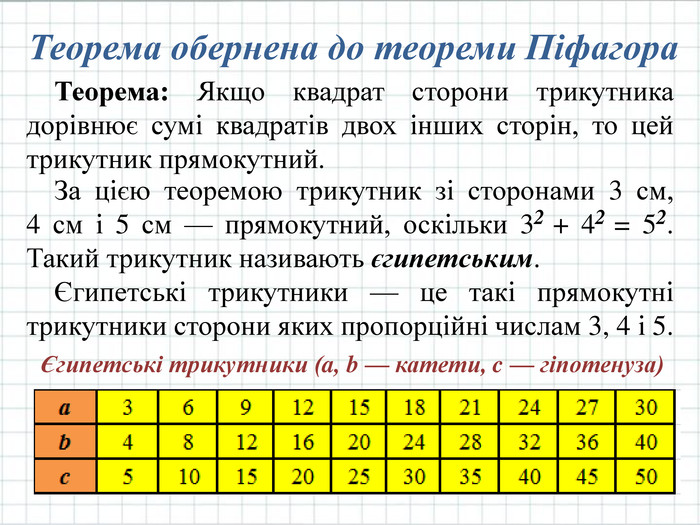
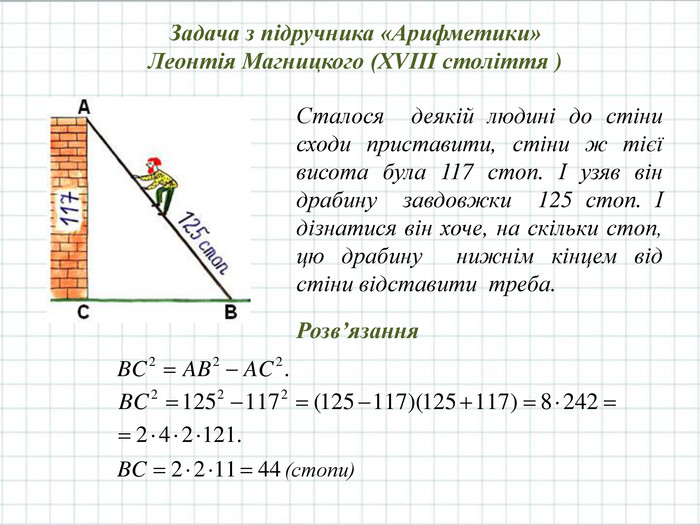
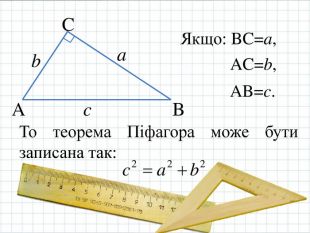
Презентація призначена для використання на уроці при вивченні нової теми "Теорема Піфагора" з геометрії у 8 класі. Містить основний теоретичний матеріал, старовинні задачі та цікаву інформацію.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




















-

Kлачик Альона Ярославівна
07.01.2025 в 09:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Богдан Галина Анатоліївна
27.02.2023 в 08:44
Дуже гарно.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тодоренко Оксана Василівна
20.02.2023 в 18:32
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стефаник Алла Миколаївна
08.02.2023 в 19:07
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Стахеєва Анна
31.01.2023 в 08:53
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
30.01.2023 в 21:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Котовський Євгеній
15.01.2023 в 22:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шама Олена
10.02.2022 в 20:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пилипенко Ганна Сергіївна
28.01.2022 в 09:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гаврус Наталя Анатоліївна
12.01.2021 в 07:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 7 відгуків