Презентація "Теорема синусів. Теорема косинусів. Розв'язування задач"
Про матеріал
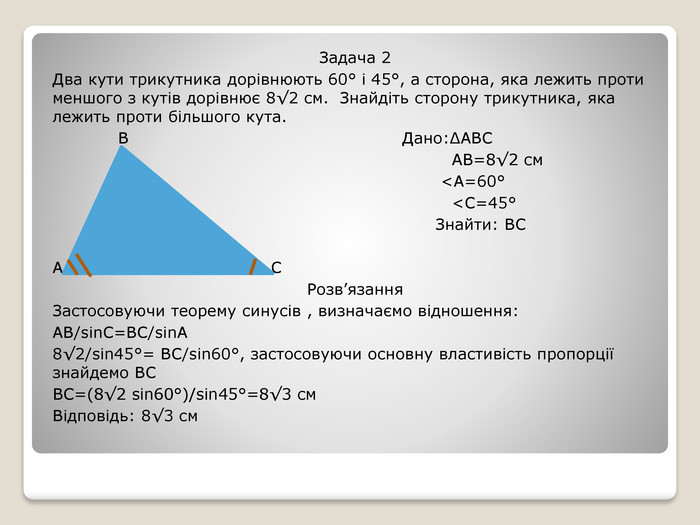
Основні задачі, які розглядаються в даній темі. Можна використовувати як допомогу при вивченні зазначених теорем Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку