Урок " Конус, його елементи. Бічна та повна поверхня конуса "
Тема уроку. Конус, його елементи. Бічна та повна поверхня конуса.
Мета уроку:
Навчальна: перевірити рівень засвоєння попереднього навчального матеріалу, ввести поняття конуса, його елементів, розглянути конус як тіло обертання, вивчити формули для площі бічної поверхні та повної поверхні конуса, сформувати вміння застосовувати знання під час розв’язування прикладних задач, показати зв'язок теми з навколишнім світом.
Розвиваюча: розвивати пізнавальний інтерес, навички колективної праці, уміння використовувати сформовані знання, навики і вміння в різних ситуаціях, розвивати культуру мовлення, логічне мислення, пам'ять, вміння раціонально використовувати час та оволодівати принципами організації праці, допитливість, ініціативність.
Виховна: виховувати працелюбність, прививати бажання мати якісні глибокі знання, доводити почату роботу до кінця, виховувати зібраність, організованість, відповідальність, увагу, вміння співпрацювати в колективі.
Тип уроку: комбінований.
Форми роботи: інтерактивні технології в навчанні.
Матеріально-технічне забезпечення та дидактичні засоби: моделі геометричних фігур, таблиці, презентації, мультимедійне обладнання, креслярські прилади.
Хід уроку
І. Організаційний момент
ІІ. Перевірка домашнього завдання. Активізація пізнавальної діяльності
ІІІ. Формулювання теми і мети уроку
Видатний французький архітектор Ле Корбюзі говорив : « Я думаю, що ніколи до цього часу ми не жили в такий геометричний період. Все навколо – геометрія». І справді, світ, в якому ми живемо, наповнений геометрією будинків і вулиць, творіннями природи і людини. Геометрія виявляється скрізь, де потрібна найменша точність у визначенні форми і розмірів. Техніку, інженеру, робітнику, архітектору – всім необхідна геометрична уява. Тіла обертання знаходять широке застосування у повсякденному житті, науці, техніці.
Сьогодні ми поповнимо свої знання про тіла обертання а також продемонструємо зв'язок математичної теорії з практикою.
Для успішного проведення уроку потрібні: концентрація уваги, зосередженість, налаштування на позитивну роботу.
Почнемо із вправи на увагу.
Дивимось на екран і запам’ятовуємо все, що зображено на слайді 10 секунд:
Вчитель пропонує дати відповіді на питання:

Вчитель. Молодці! Добре справились із завданням.
IV. Мотивація навчальної діяльності
Сьогодні на уроці нам належить виконати дуже важливу, і, сподіваюся, цікаву роботу. А з чим вона пов'язана, спробуйте здогадатися, подивившись на репродукцію картини Шишкіна «Корабельний гай» .
Запитання вчителя: «Як ви гадаєте, який зв'язок між цією картиною і ось такою фігурою?» (Демонструється модель конуса ). Відповідь: «На картині – сосни, в руках учителя – конус, у перекладі з грецької – соснова шишка».

Отже, який геометричний об'єкт ми будемо вивчати сьогодні? Правильно, це конус. Як же буде звучати тема нашого уроку? Запишіть її в робочих зошитах.
Скажіть, а що саме навело вас на думку про конус? Чи чули ви, що латинське слово «conus» запозичене з грецької мови (konos - соснова шишка). Форму конуса часто можна розглянути в оточуючих нас предметах і в природі.
Наведіть приклади.
А тепер давайте подивимося презентацію про конуси навколо нас, яку підготували дівчата.
ПРЕЗЕНТАЦІЯ
Діти, уявіть собі таку ситуацію. Що ви є власником восьми кафе. Вам повідомили, що через два дні до вас приїде перевірка, яка оглядатиме пожежні щити (слайд), а у вас не вистачає конусних відер, купити ніде, замовити часу не має, але є у вас лист заліза 2 м × 1,5 м і є робітник який знає зварювальну справу. Отже, перед вами постає задача.
Скільки можна виготовити конічних відер із цього листа? Якщо відомо, що діаметр відра становить 28 см, а висота – 39 см.
Чи можете ви зараз вирішити це завдання?
Що необхідно знати для її вирішення?
Які ж цілі ми поставимо, щоб ми змогли вирішити завдання? (вивчити поняття конуса, його основні елементи і формули для обчислення площі поверхні конуса).
Подивіться, будь ласка, на геометричні фігури на дошці. Поділіть їх на дві групи. За якою ознакою ви їх розділили? Вірно, одні геометричні фігури на площині, інші в просторі (їх називають геометричними тілами).
З яким тілом обертання ви вже добре знайомі? (Циліндр)
Давайте пригадаємо, що таке циліндр і з яких елементів він складаеться.
ВПРАВА LearningApps
Діти, як ви гадаєте навіщо ми пригадали з вами елементи циліндра?
Так діти, конус має майже всі елементи, що і циліндр.
Давайте розглянемо конус ( слайд )
Конусом називається тіло, яке складається з круга, точки яка не лежить в площині цього круга, і всіх відрізків, що сполучають задану точку з точками круга.
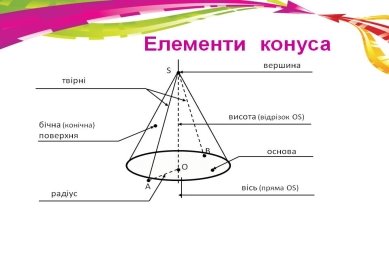
Дослідження моделі конуса (робота в парах)
-У вас на столі модель конуса. Обережно розгорніть її і дайте відповідь на питання, які є у кожного на парті. Ви можете радитися в парі 3 хвилини:
1. З яких частин складається поверхня конуса? (З кола радіуса r і кругового сектора)
2. Чому дорівнює радіус кругового сектора? (довжині твірної)
3. Що ви можете сказати про довжину кола основи конуса і довжину дуги кругового сектора? (Вони рівні)
 Розгорткою бічної поверхні конуса є круговий сектор, радіус якого дорівнює твірній конуса, а довжина дуги сектора – довжині кола основи конуса. Площею бічної поверхні конуса будемо вважати
Розгорткою бічної поверхні конуса є круговий сектор, радіус якого дорівнює твірній конуса, а довжина дуги сектора – довжині кола основи конуса. Площею бічної поверхні конуса будемо вважати
площу її розгортки.
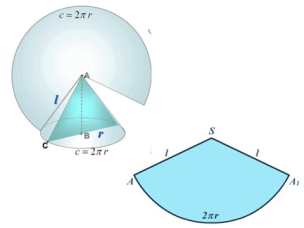
Виразимо площу бічної поверхні конуса Sбіч. через його твірну ℓ і радіус основи R.

Площа бічної поверхні конуса дорівнює добутку половини
довжини кола основи на твірну.
Так як довжина кола основи дорівнює: с = 2πR, то
Sбіч. = πRℓ.
Основою конуса є круг, тому площа основи конуса дорівнює:
Sосн. = πR2.
 Площею повної поверхні конуса називається сума площ бічної
Площею повної поверхні конуса називається сума площ бічної
поверхні та основи. Для обчислення площі повної поверхні конуса Sк одержуємо формулу: Sпов = Sбіч + Sосн
Sпов = πRℓ + πR2
V. Формування вмінь
Розв’язати задачі:
Повертаємося до практичної задачі, розглянутої на початку уроку, яка зводиться до знаходження площі бічної поверхні конуса.
Розв’язання:

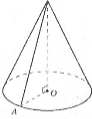
ОА = R = 14 см, SO = 39 см.
Із трикутника SOA (![]() SOA = 90°) отримаємо за теоремою Піфагора:
SOA = 90°) отримаємо за теоремою Піфагора:
ℓ = SA = ![]()
ℓ = ![]() =
= ![]()
Відомо, що ![]() тоді
тоді ![]()
Площу листа можна обчислити за формулою:
Sлиста = ![]() отже
отже
Sлиста = 200 · 150 = 30000 см2.
![]()
Який висновок ми зможемо зробити? Скільки можна зробити відер?
Відповідь: 16 відер.
Д. Пойа казав: « Вміння розв’язувати задачі – це практичне мистецтво, подібне до плавання чи катання на лижах, чи грі на фортепіано. Навчитися цьому можна лише постійно тренуючись…».
От і ми з вами потренуємося розв’язувати задачі на обчислення Sбіч. та Sпов. конуса.
Деякі учні працюватимуть на картках.
Задача ( слайд )
- Святковий торт має форму конуса. Площа його основи дорівнює 36π дм2, а твірна 10 дм. Чому дорівнює його бічна поверхня. Чи вміститься він на підносі діаметром 12дм.

Дано: Sосн = 36π дм2
l = 10 дм
Sбіч --- ?
![]()
R = √
Задача на слайді
Самостійно один учень біля дошки.
- Висота конуса дорівнює 12см, радіус – 5см. Знайдіть площу його повної поверхні та бічної
- Твірна конуса дорівнює 5см, висота – 4см. Знайдіть площу його повної поверхні.
VI. Рефлексія
Урок добігає кінця. Чи досягли ми цілей поставлених нами на початку уроку. Що нового ми дізналися? Чому навчилися?
Для того, щоб підвести підсумок вивченого, розв’яжемо кросворд.
Розв’язати кросворд
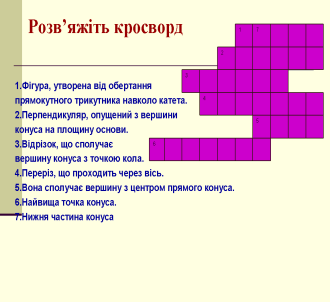
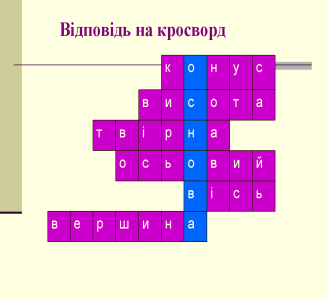
VII. Підсумки уроку
(Демонструється фрагмент із мультфільму «Жадный богач»).
Р. Декарт говорив: «Теорія без практики мертва і безплідна,
практика без теорії неможлива…». Справді, ми побачили і в черговий раз переконалися на уроці, що практика без теорії неможлива.
Також з’ясували, що знання з цієї теми стануть нам у пригоді в житті та у майбутній вашій професії.
VIIІ. Домашнє завдання
А щоб краще засвоїли дану тему потрібно вам виконати домашнє завдання.
1. Вивчити формули.
2. Знайти площу бічної поверхні конуса, радіус основи якого дорівнює 3 см, висота – 4 см.
3. Виміряти площу повної поверхні будь-якого предмета, який має форму конуса.


про публікацію авторської розробки
Додати розробку
