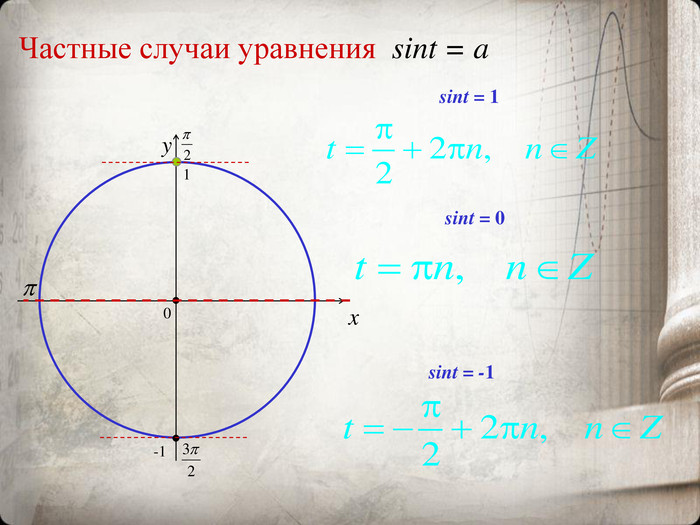
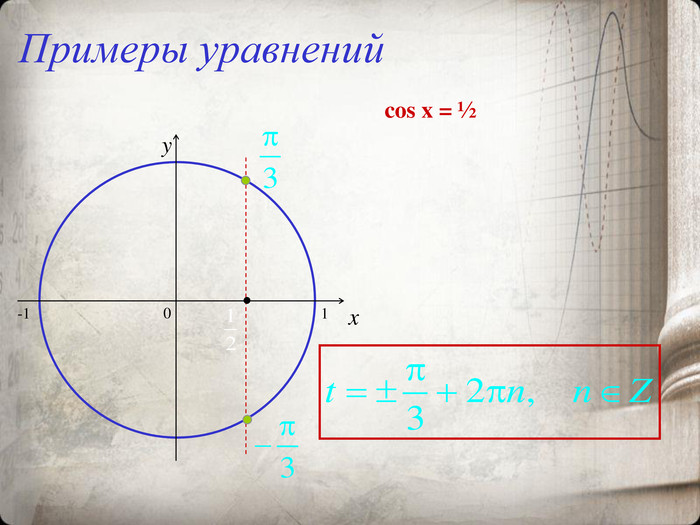
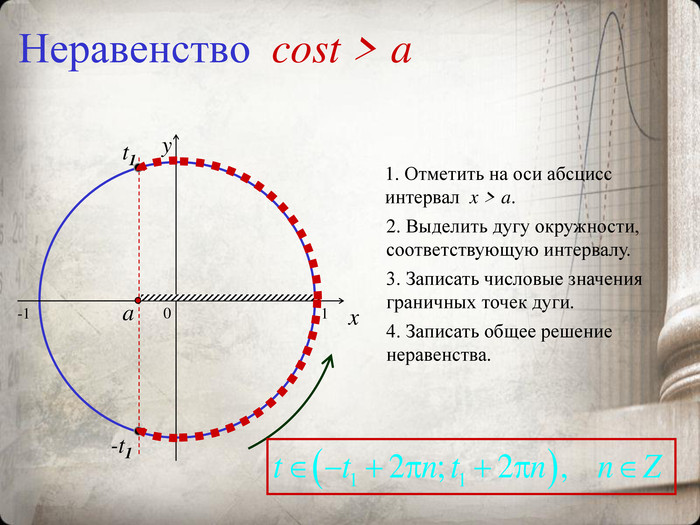
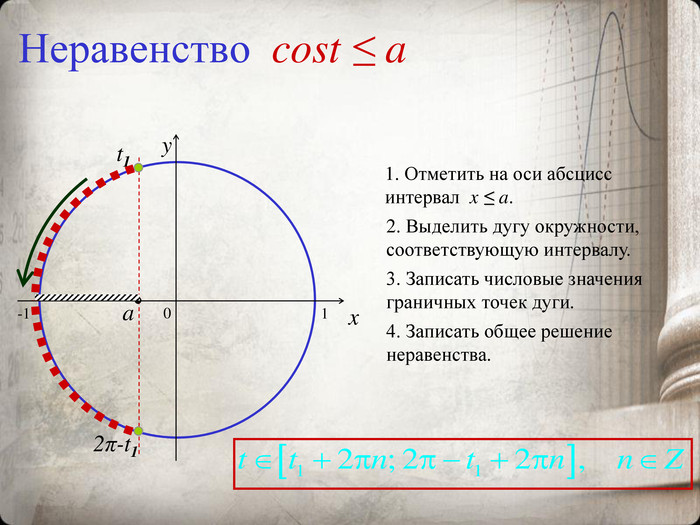
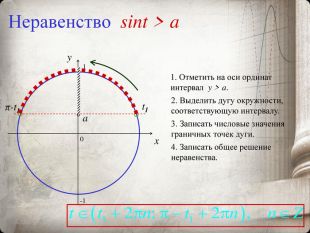
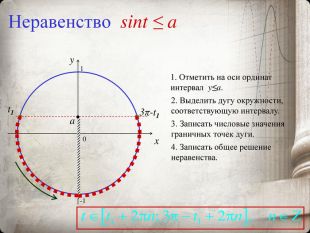
Презентация "Тригонометрические уравнения и неравенства"
Про матеріал
Дану презентацию можна використовувати під час узагальнення теми "Тригонометричні рівняння та нерівності" Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



![Арксинус и его свойства Арксинусом числа a (|a|≤1) называется такой угол α, принадлежащий отрезку [-π/2; π/2], синус которого равен a. Обозначается этот угол arcsin a. Читается так: угол, синус которого равен a . Арксинус и его свойства Арксинусом числа a (|a|≤1) называется такой угол α, принадлежащий отрезку [-π/2; π/2], синус которого равен a. Обозначается этот угол arcsin a. Читается так: угол, синус которого равен a .](/uploads/files/740686/209054/225142_images/3.jpg)
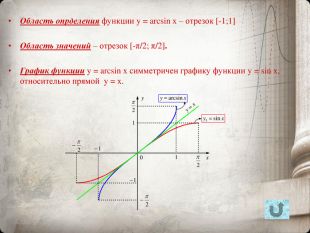
![Область опрделения функции y = arcsin x – отрезок [-1;1] Область значений – отрезок [-π/2; π/2]. График функции y = arcsin x симметричен графику функции y = sin x, относительно прямой y = x. Область опрделения функции y = arcsin x – отрезок [-1;1] Область значений – отрезок [-π/2; π/2]. График функции y = arcsin x симметричен графику функции y = sin x, относительно прямой y = x.](/uploads/files/740686/209054/225142_images/4.jpg)
![Арккосинус и его свойства Арккосинусом числа a (|a|≤1) называется такой угол α, принадлежащий отрезку [0; π], косинус которого равен a. Обозначается этот угол arccos a. Читается так: угол, косинус которого равен a . Арккосинус и его свойства Арккосинусом числа a (|a|≤1) называется такой угол α, принадлежащий отрезку [0; π], косинус которого равен a. Обозначается этот угол arccos a. Читается так: угол, косинус которого равен a .](/uploads/files/740686/209054/225142_images/5.jpg)
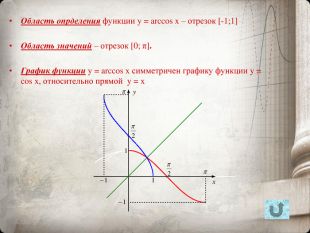
![Область опрделения функции y = arccos x – отрезок [-1;1] Область значений – отрезок [0; π]. График функции y = arccos x симметричен графику функции y = cos x, относительно прямой y = x Область опрделения функции y = arccos x – отрезок [-1;1] Область значений – отрезок [0; π]. График функции y = arccos x симметричен графику функции y = cos x, относительно прямой y = x](/uploads/files/740686/209054/225142_images/6.jpg)