Презентація "Тригонометричні функції і рівняння"

Урок узагальнення та систематизації Тригонометричні функції. Тригонометричні рівняння. ЖЕЛІЗКО Л. В.,ВЧИТЕЛЬ МАТЕМАТИКИ

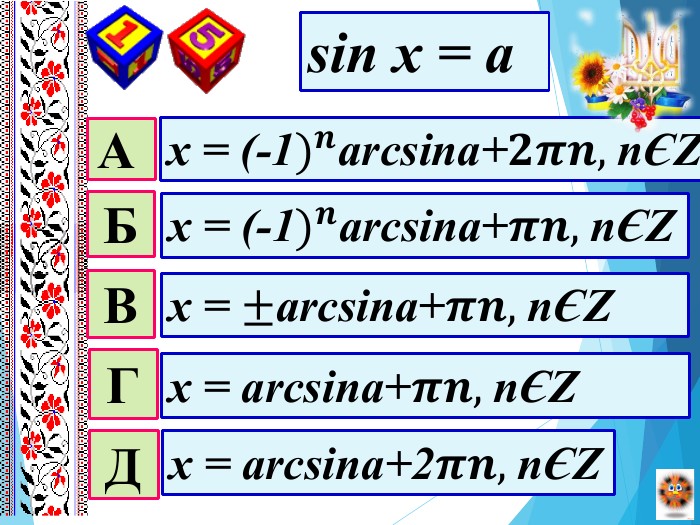
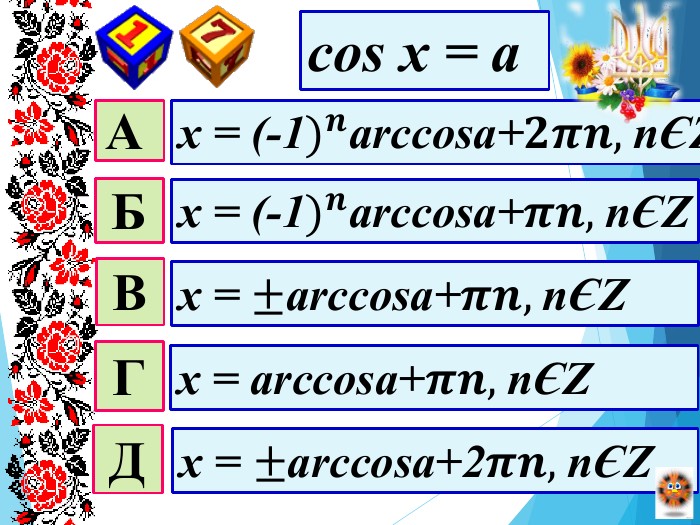
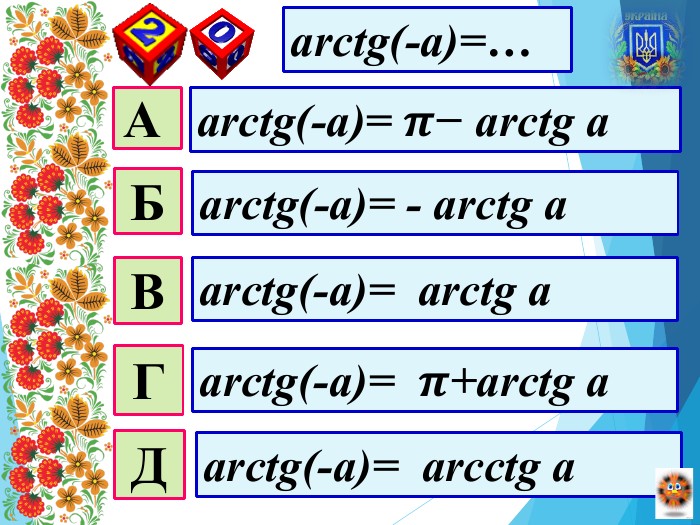
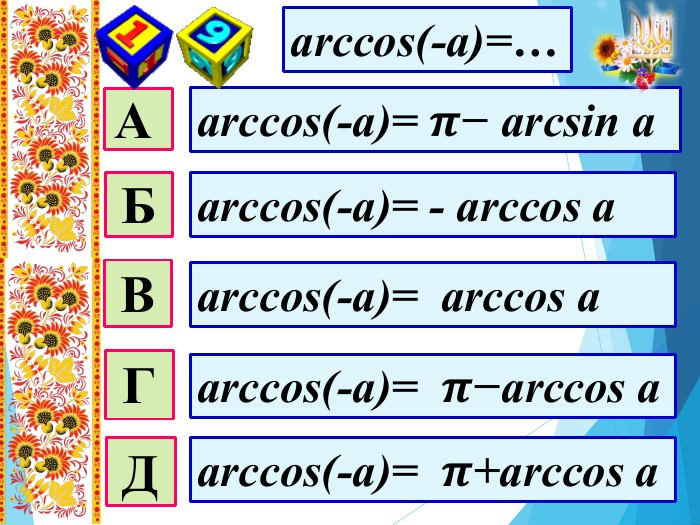
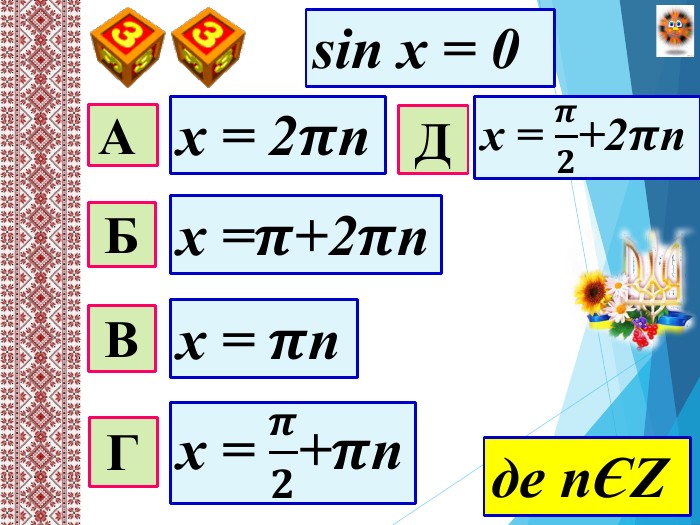
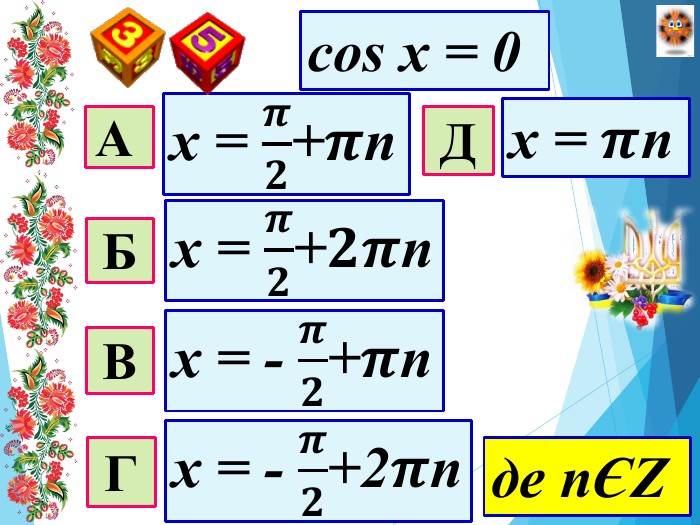
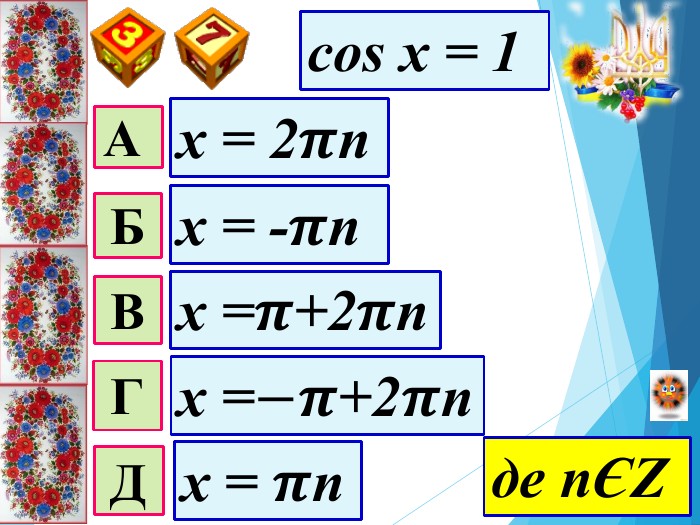
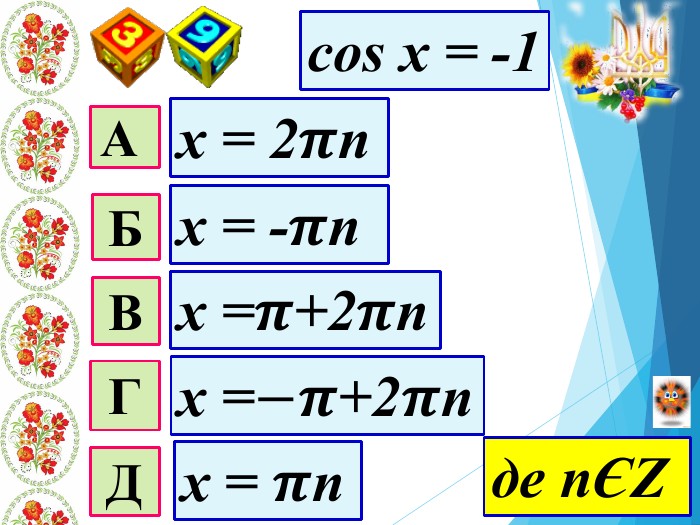
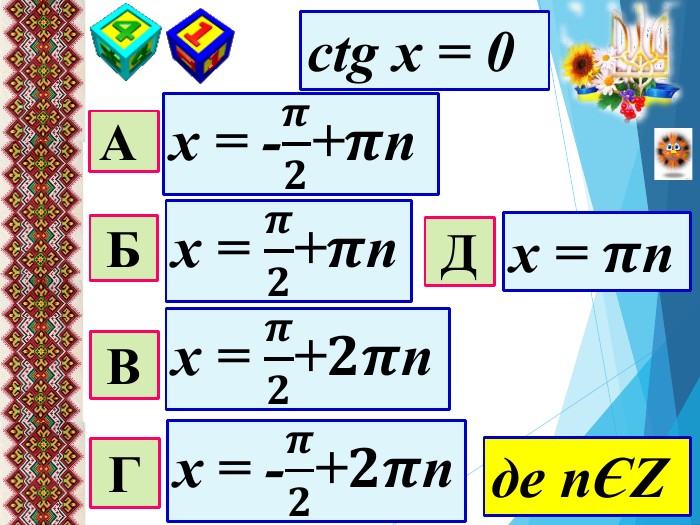
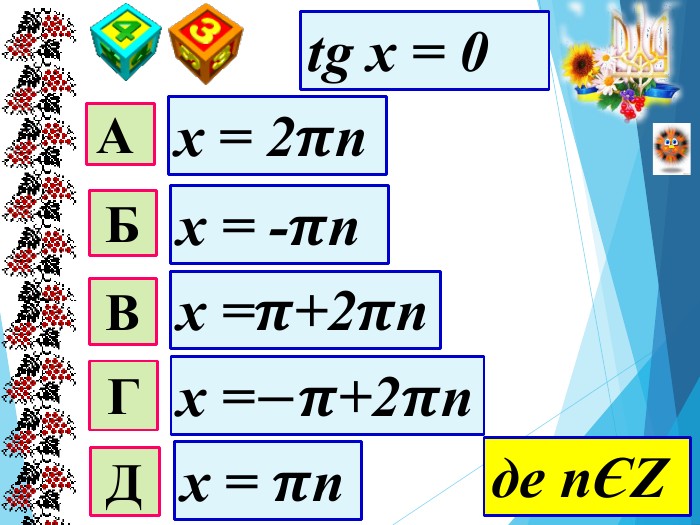
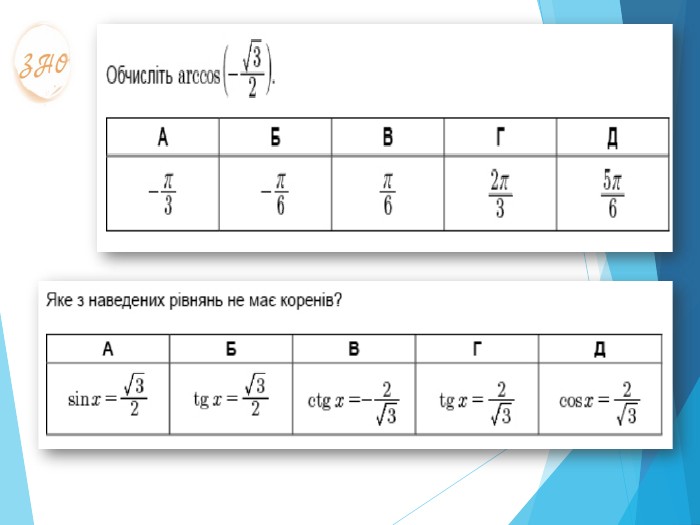
Мета уроку: Удосконалити вміння правильно розв′язувати найпростіші тригонометричні рівняння; однорідні рівняння та рівняння, що зводяться до однорідних; вдосконалювати вміння розв’язувати рівняння методом заміни змінних;Розвивати просторову уяву; навички самоконтролю та взаємоконтролю, логічне мислення, пам’ять, вміння аналізувати ситуацію; творчі здібності та пізнавальну активність;Виховувати почуття відповідальності та старанності в навчанні, увагу, активність, інтерес до предмету, правильне математичне мовлення.

Формування компетентностей: Предметна: узагальнити знання учнів з теми; удосконалити практичні уміння та навички розв'язувати тригонометричні рівняння , показати практичне застосування теми при розв’язуванні завдань при підготовці до ЗНО. Ключові компетентності:-математична компетентність – оперувати математичними термінами та формулами.- спілкування державною мовою - доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку.-уміння вчитися впродовж життя - усвідомлювати цінність нових знань і вмінь.-соціально - громадянську компетентність,-ініціативність та підприємливість;

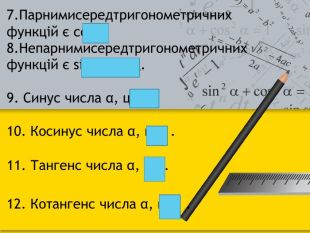
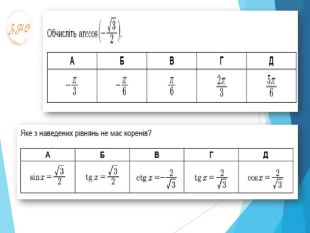
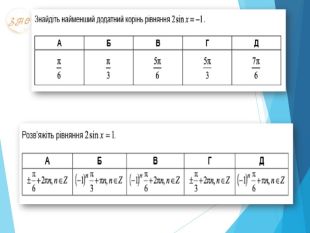
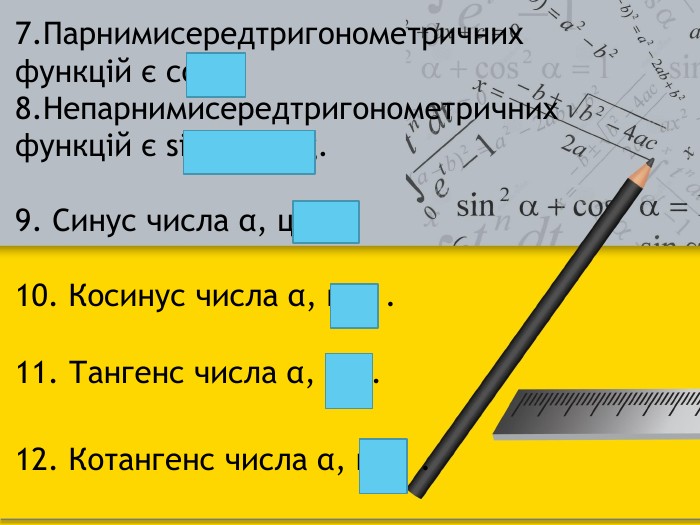
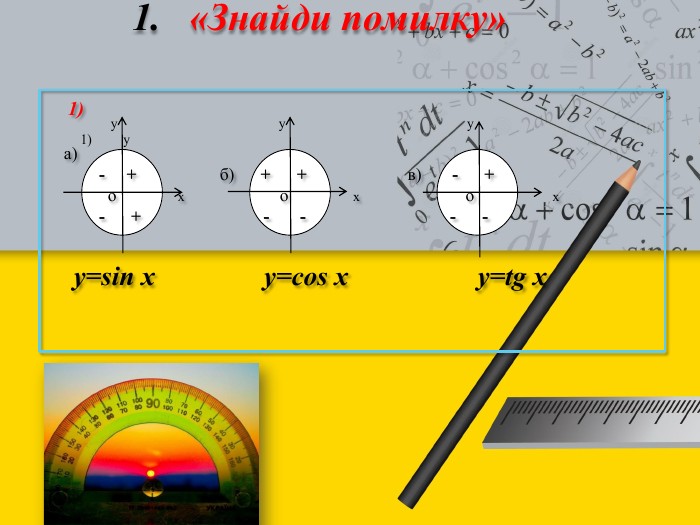
Технологія: «Закінчи речення»Якщо α = 210°, то кут α є кутом ІІІ чверті.2. Якщо α = 150°, то кут α є кутом ІІ чверті.3. Якщо α = π/3, то кут α є кутом І чверті.4. Якщо α = -2π/5, то кут α є кутом ІV чверті.5. Якщо градусна міра кута 120°, то його радіанна міра дорівнює 2π/3.6. Якщо радіанна міра кута 7π/6, то його градусна міра 210°.

7. Парнимисередтригонометричнихфункцій є cos.8. Непарнимисередтригонометричнихфункцій є sin, tg, ctg.9. Синус числа α, це у .10. Косинус числа α, цех .11. Тангенс числа α, цеух.12. Котангенс числа α, цеху . 

«Знайди помилку» 1) а) - + б) + + в) - + о х о х о х - + - - - - у=sin x у=cos x у=tg x

Знайдіть помилку і назвіть правильну відповідь

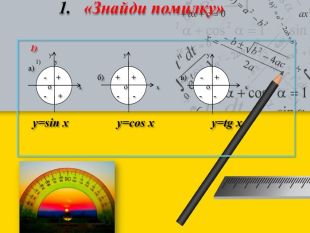
Знайти відповідність:1) y=sinx перенести на 2 од. вгору2) y=sinx перенести на 2 од. вниз3) y=sinx перенести на π/3 праворуч4) y=sinx перенести на π/3 ліворуч5) y=sinx перенести на π/3 праворучі розтягнути вздовж осі Оу у 2 рази6) y=sinx перенести на π/3 ліворуч і стиснути вздовж осі Ох у 2 разиу=sinx+2у=sinx–2 у=sin(2x+π/3)у=sin(x+π/3) у=2sin(x-π/3)у=sin(x-π/3)

ТРИГОНОМЕТРИЧНИЙ ТРЕНАЖЕР

А  БВГДsin х = aх = (-1)𝒏arcsina+𝝅𝒏, nЄZ х = ±arcsina+𝝅𝒏, nЄZ х = (-1)𝒏arcsina+𝟐𝝅𝒏, nЄZ х = arcsina+𝝅𝒏, nЄZ х = arcsina+2𝝅𝒏, nЄZ r

А  БВГДcos х = aх = (-1)𝒏arccosa+𝟐𝝅𝒏, nЄZ х = (-1)𝒏arccosa+𝝅𝒏, nЄZ х = ±arccosa+𝝅𝒏, nЄZ х = arccosa+𝝅𝒏, nЄZ х = ±arccosa+2𝝅𝒏, nЄZ r

А  БВГДarcsin(-a)=…arcsin(-a)= 𝝅− arcsin a arcsin(-a)= - arcsin aarcsin(-a)= arcsin aarcsin(-a)= arccos aarcsin(-a)= arctg(-a)r

А  БВГДarctg(-a)= arcctg aarctg(-a)=…arctg(-a)= - arctg aarctg(-a)= 𝝅− arctg a arctg(-a)= arctg aarctg(-a)= 𝝅+arctg a r

А  БВГДarccos(-a)=…arccos(-a)= 𝝅− arcsin a arccos(-a)= - arccos aarccos(-a)= arccos aarccos(-a)= 𝝅−arccos a arccos(-a)= 𝝅+arccos a r

А  БВГДtg х = aх = (-1)𝒏arctga+𝟐𝝅𝒏, nЄZ х = (-1)𝒏arctga+𝝅𝒏, nЄZ х = ±arctga+𝝅𝒏, nЄZ х = arctga+𝝅𝒏, nЄZ х = arctga+2𝝅𝒏, nЄZ r

А  БВГДarcсtg(-a)=…arcctg(-a)= 𝝅− arctg a arcctg(-a)= - arcctg aarcctg(-a)= arcctg aarcctg(-a)= 𝝅−arcctg a arcctg(-a)= arctg ar

А  БВГДctg х = aх = (-1)𝒏arcctga+𝟐𝝅𝒏, nЄZ х = (-1)𝒏arcctga+𝝅𝒏, nЄZ х = ±arcctga+𝝅𝒏, nЄZ х = arcctga+𝝅𝒏, nЄZ х = arcctga+2𝝅𝒏, nЄZ r

А  БВГДsin х = 1х = 𝝅𝟐+2𝝅n  х = - 𝝅𝟐+2𝝅n  х = 𝝅n  х = 𝝅𝟐+𝝅n  х =𝝅+2𝝅n  де nЄZ r

А  БВГДsin х = -1х = - 𝝅𝟐+2𝝅n  х = 𝝅𝟐+2𝝅n  х = 𝝅𝟐+𝝅n  х =𝝅+2𝝅n  х = 𝝅n  де nЄZ r

А  БВГДsin х = 0х = 𝝅n  х = 2𝝅n  х =𝝅+2𝝅n  х = 𝝅𝟐+𝝅n  х = 𝝅𝟐+2𝝅n  де nЄZ r

А  БВГДcos х = 0де nЄZ х = 𝝅𝟐+𝝅n  х = 𝝅𝟐+𝟐𝝅n  х = - 𝝅𝟐+𝝅n  х = - 𝝅𝟐+2𝝅n  х = 𝝅n  r

А  БВГДcos х = 1де nЄZ х = 𝝅n  х = 2𝝅n  х = -𝝅n  х =𝝅+2𝝅n  х =−𝝅+2𝝅n  r

А  БВГДcos х = -1де nЄZ х = 2𝝅n  х = -𝝅n  х =𝝅+2𝝅n  х =−𝝅+2𝝅n  х = 𝝅n  r

А  БВГДctg х = 0де nЄZ х = 𝝅𝟐+𝝅n  х = -𝝅𝟐+𝝅n  х = 𝝅𝟐+𝟐𝝅n  х = -𝝅𝟐+𝟐𝝅n  х = 𝝅n  r

А  БВГДtg х = 0де nЄZ х = 2𝝅n  х = -𝝅n  х =𝝅+2𝝅n  х =−𝝅+2𝝅n  х = 𝝅n  r

ТРИГОНОМЕТРИЧНА дуель

Знати , вміти і творити, щоб ЗНО змогли підкорити!2012р. Розвязати рівняння. tg3x = √𝟑 А) х= π 𝟔 +𝝅𝒏,𝒏є 𝒁 Б) ) х= π 𝟑 +𝝅𝒏,𝒏є 𝒁В) х= π 𝟗 +πn 𝟑,𝒏є 𝒁Г) ) х= π 𝟗 +2πn 𝟑,𝒏є 𝒁 Д) ) х= π 𝟗 +𝝅𝒏,𝒏є 𝒁Б) 

Інтерактивна вправа «Не хочу хвалитися,але я…»1. Добре знаю…..2. Добре вмію…..3. Найкраще засвоїв….4. Найкраще мені вдається….5. Вмію розв’язувати….6. Вмію знаходити….

ДОМАШНЄ ЗАВДАННЯ: Повторити §11-15 ; виконати домашню самостійну роботу;підготуватися до контрольної роботи.