Самостійна робота "Циліндр"

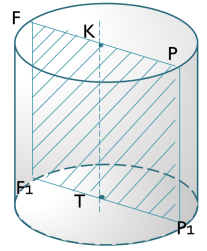
1(½б).Скільки основ у циліндра?Які геометричні фігури,що є основами циліндра.

2(1б).Назвіть геометричну фігуру, при обертанні якої утворюється циліндр.Назвіть пряму,що являється віссю циліндра.

3(2б).Назвіть центри основ циліндра, радіуси, діаметри основ, висоту  та твірну циліндра. Запишіть формулу для обчислення площі основи S_осн циліндра

4(1б).Яка фігура на зображенні циліндра називається його осьовим перерізом. Запишіть формулу, за якою можна обчислити площу цього перерізу.

5(1б).Запишіть формулу для обчислення площі бічної поверхні  та площі повної поверхні циліндра.

6(½б).Запишіть формулу для обчислення об’єму даного циліндра.

7(6б).Обчисліть діагональFP₁,площу осьового S_{перерізу}, S_осн, S_біч, S_повна , V_цил, якщо  діаметр основи циліндра дорівнює 12 см, а твірна циліндра  дорівнює 5 см.

1(½б).Скільки основ у циліндра? Які геометричні фігури,що є основами циліндра.

2(1б).Назвіть геометричну фігуру, при обертанні якої утворюється циліндр. Назвіть пряму,що являється віссю циліндра.

3(2б).Назвіть центри основ циліндра, радіуси, діаметри основ,висоту  та твірну циліндра. Запишіть формулу для обчислення площі основи S_осн циліндра

4(1б).Яка фігура на зображенні циліндра називається його осьовим перерізом. Запишіть формулу, за якою можна обчислити площу цього перерізу.

5(1б).Запишіть формулу для обчислення площі бічної поверхні  та площі повної поверхні циліндра.

6(½б).Запишіть формулу для обчислення об’єму даного циліндра.

7(6б).Обчисліть діагональ DG₁, площу осьового S_{перерізу}, S_осн, S_біч, S_повна , V_цил, якщо  діаметр основи циліндра дорівнює 8 см, а твірна циліндра  дорівнює 6 см.