Урок. Тема: "Перерізи циліндра"

Дата ______________

Група _____________

- формувати знання про перерізи циліндра; вчити виконувати побудови перерізів, знаходити їх елементи, площі;

- усвідомити алгоритм побудови перерізів циліндра; розвивати увагу та критичне мислення, креслярські здібності.

- сприяти розвитку інтересу до предмету геометрія. Виховувати культуру спілкування, дисциплінованість.

Хід уроку

І.    Організаційний момент:

- перевірка наявності учнів;

- перевірка готовності учнів до уроку.

ІІ Мотивація навчальної діяльності учнів.

Викладач демонструє різні перерізані циліндри.

Проблемне питання

Яке геометричне  тіло розрізали?

Про що піде мова на сьогоднішньому уроці? (учні формулюють тему і мету уроку)

Актуалізація опорних знань:

Мозковий штурм

1.   Наведіть приклади побутових предметів, які мають форму циліндра.
2.   Користуючись мал., назвіть:

а) радіус циліндра; б) висоту циліндра; в) вісь циліндра; г) твірну циліндра.

3.   Які властивості мають основи циліндра?
4.   Які властивості мають твірні циліндра?
5.   Яку властивість має вісь циліндра щодо: а) його основ; б) його твірних?
6.   Часто висотою прямого кругового циліндра називають відрізок, що з'єднує центри основ. Яку властивість має висота циліндра щодо: а) твірних; б) основ?
7.   Із стопки картону взяли аркуш і вирізали круг. Дістали циліндр з дуже малою висотою. Як практично визначити його висоту?
8.   Назвіть властивості циліндра, які однакові з властивостями прямої призми.
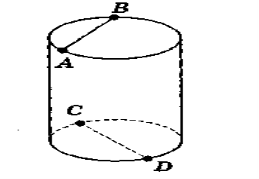
9.   Як знайти відстань між прямими АВ і CD (рис. 102)?

ІІІ Виклад нового матеріалу.

Дослідницький метод навчання.

Експеримент. (учням пропоную пластилінові циліндри, учні їх розрізають різним чином. Намагаються дати назву утвореному перерізу та з’ясувати фігуру яка в перерізі)

 

 робимо висновки

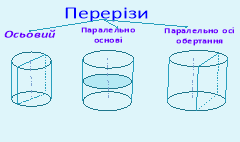
Викладач поетапно будує перерізи циліндра.

(Переріз, утворений площиною, що проходить через вісь циліндра, називається осьовим перерізом циліндра.

Осьовий переріз циліндра - прямокутник зі сторонами, що дорівнюють висоті циліндра і діаметру його основи.

Переріз циліндрів площиною, паралельною його осі, є прямокутником.

Переріз циліндра площиною, паралельною основам циліндра, є кругом, який дорівнює основі.)

ІІІ  Закріплення вивченого матеріалу.

Запитання до класу

1) Що є перерізом циліндра площиною, яка:

а) паралельна основам циліндра;

б) паралельна осі циліндра?

2) Заповніть пропуски.

а) Переріз циліндра площиною, яка перпендикулярна до основи, є..., дві сторони якого - ..., а дві інші - ...

б) Переріз циліндра площиною, яка проходить через його вісь, називається...

в) Переріз циліндра площиною, перпендикулярною до його осі, є..., що дорівнює основі.

г) Площина, паралельна площині основи циліндра, перетинає його бічну поверхню по..., що дорівнює...

(Відповідь, а) ...прямокутник... твірні циліндра... паралельні хорди основ; б)...осьовим перерізом; в) круг; г) ...колу... колу основи.)

Розв’язування задач.

Усно або письмово (в залежності від рівня підготовки учнів обираю кількість і складність).

1.Знайти площу осьового перерізу циліндра, якщо радіус основи 5см, а твірна12см (Відповідь: 120см²)

2.Знайдіть діагональ осьового перерізу циліндра, якщо висота циліндра 3см, а діаметр основи 4см. (Відповідь: 5см)

3.Чому дорівнює площа осьового перерізу циліндра, якщо радіус основи 6см. (Відповідь 36πсм²) 

4.Знайдіть довжину кола основи, якщо осьовий переріз циліндра є квадрат площа якого 25см² (Відповідь 10πсм)

5.Висота циліндра 6 см, радіус основи 5 см. Знайдіть периметр перерізу, проведеного паралельно осі циліндра на відстані 4 см від неї. (Відповідь. 24 см.)

6.Висота циліндра дорівнює 10 см. Площа перерізу циліндра площиною, паралельною осі циліндра і віддаленою на 9 см від неї, дорівнює 240 см². Знайдіть радіус циліндра. (Відповідь. 15 см.)

IV Домашнє завдання

§ 6, п. 52, 53; контрольні запитання 1-4; розв'язати задачі № 3-5 (с. 95)

IVПідведення підсумків «паркан відвертості»