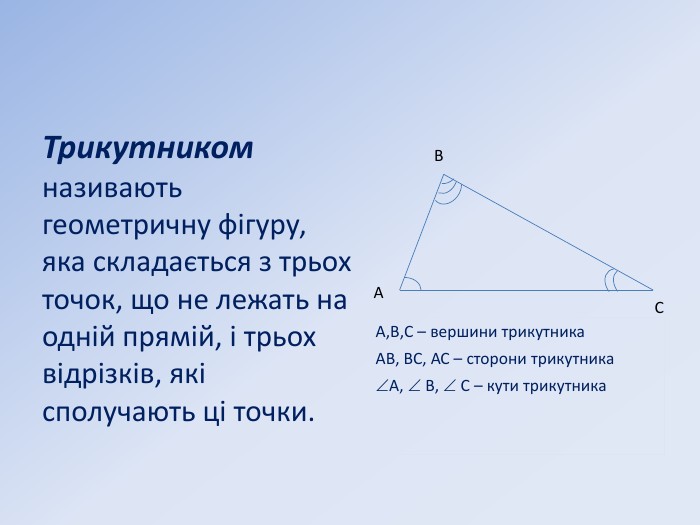
Презентація "Трикутники"

Тема: «Трикутники»

Історія трикутника Уже кілька тисяч років тому єгиптяни знали, що коли сторони трикутника дорівнюють 3, 4 і 5 одиничним відрізкам, то такий трикутник прямокутний. Землеміри Стародавнього Єгипту для побудови прямого кута ділили мотузку вузликами на 12 рівних частин і кінці зав’язували. Потім мотузку розтягували на землі так, щоб утворився трикутник зі сторонами по 3, 4 і 5 поділок. Більший з кутів утвореного трикутника – прямий. Ребра бічних граней єгипетських пірамід утворюють майже рівносторонні трикутники. Слово “трикутник” античного походження. Знак  для позначення трикутників запропонував ще в І столітті давньогрецький вчений Герон. Знак  Почали застосовувати в ІV столітті

Історія трикутника Трикутник – найпростіша фігура: три вершини й три сторони. Але під час вивчення трикутника утворилася окрема наука - тригонометрія, у якій метричні властивості трикутника виражаються через функції його кутів. Ця наука виникла на основі практичної необхідності у вимірюванні ділянок, складанні карт місцевості, конструюванні машин і механізмів. Перші відомості про трикутник та його властивості ми знаходимо в єгипетських папірусах, яким більше 4000 років. У них зокрема, згадується спосіб знаходження площі рівнобедреного трикутника. Через 2000 років у Стародавній Греції вивчення властивостей трикутника досягає високого рівня. У XV—XVI ст. з'явилася величезна кількість досліджень властивостей трикутника, які ввійшли в розділ планіметрії, що одержав назву «Нова геометрія трикутника». Великий внесок у розвиток геометрії трикутника внесли мате­матики XIX—XX ст.: Лемуан, Брокар, Тебо й ін.

Трикутником називають геометричну фігуру, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які сполучають ці точки. А,В,С – вершини трикутника АВ, ВС, АС – сторони трикутника А,  В,  С – кути трикутника А В С

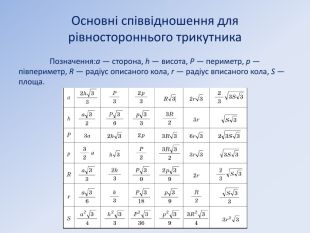
Класифікація трикутників Залежно від довжин сторін різносторонні (Трикутник в якого всі сторони мають різну довжину, називається різностороннім трикутником) рівносторонні (Трикутник, три сторони якого рівні, називається рівностороннім трикутником.) рівнобедрені (Трикутник, дві сторони якого рівні, називається рівнобедреним.Третя сторона - основа, рівні сторони – бічні сторони.) різносторонній рівносторонній рівнобедрений

Класифікація трикутників Залежно від градусної міри кутів: - гострокутні ( Гострокутним називається трикутник, у якого всі три кути гострі, тобто менші за 900 ) - тупокутні (Тупокутним називається трикутник, в якого один кут тупий, тобто більший від 900 і менший від 1800 , а два інші кути є гострі . - прямокутні (Прямокутним називається трикутник в якого один кут прямий, тобто дорівнює 900 , а два інші кути гострі. У прямокутному трикутнику сторона, яка лежить проти прямого кута, називається гіпотенузою, дві інші сторони – катетами) гострокутній тупокутній прямокутний

Бісектриса трикутника Бісектрисою трикутника називається відрізок, який з’єднує вершину трикутника з точкою на протилежній стороні і ділить внутрішній кут навпіл. Три бісектриси перетинаються в одній точці, інцентрі, центрі вписаного в трикутник кола. Вписане коло — це коло, яке лежить всередині трикутника і дотикається до трьох його сторін. Бісектриса ділить протилежну сторону на відрізки, пропорційні до прилеглих сторін

Висота трикутника Висота трикутника — пряма проведена з вершини і перпендикулярна до протилежної сторони або до продовження протилежної сторони. Довжина висоти — це відстань від вершини до основи трикутника. Три висоти перетинаються в одній точці, яка назвається ортоцентром трикутника. Ортоцентр лежить всередині трикутника тоді і тільки тоді, якщо трикутник не тупокутний.

Медіана трикутника Медіана трикутника — це пряма проведена через вершину і середину протилежної сторони і ділить трикутник на два однакової площі. Три медіани перетинаються в одній точці, яка називається центроїдом трикутника. Центроїд ділить кожну медіану у співвідношенні 2:1, починаючи від вершини. О О - центроїд

Ознаки рівності трикутників Перша ознака Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам та куту між ними іншого трикутника, то такі трикутники рівні. Друга ознака Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні. Третя ознака Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.

Ознаки рівності прямокутних трикутників 1) Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні. 2) Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету і прилеглому до нього гострому куту іншого, то такі трикутники рівні. 3) Якщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та гострому куту іншого, то такі трикутники рівні. 4) Якщо гіпотенуза і катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі і катету іншого, то такі трикутники рівні.

Ознаки подібності трикутників 1) Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні. 2) Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника та кути, утворені цими сторонами, рівні, то такі трикутники подібні. 3) Якщо три сторони одного трикутника пропорційні трьом сторонам іншого трикутника, то такі трикутники подібні.

Теорема Піфагора Висновки теореми Піфагора У прямокутному трикутнику будь–який з катетів менший, ніж гіпотенуза Якщо до прямої з однієї точки проведені перпендикуляр і похила, то похила більша, ніж перпендикуляр. Рівні похилі мають рівні проекції. З двох похилих більша та, проекція якої більша.

Співвідношення між елементами сторін прямокутного трикутника Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи. Синусом гострого кута називається відношення протилежного катета до гіпотенузи. Тангенсом гострого кута називається відношення протилежного катета до прилеглого. Котангенсом гострого кута називається відношення прилеглого катета до протилежного

Основні співвідношення для рівностороннього трикутника Позначення:а — сторона, h — висота, Р — периметр, р — півпериметр, R — радіус описаного кола, r — радіус вписаного кола, S — площа.

Трикутник Паскаля Трикутник Паскаля — це геометрично, на зразок трикутника, розміщені біноміальні коефіцієнти. Це математичне поняття названо на честь Блеза Паскаля. Таку назву вживають переважно в західному світі, адже математики Індії, Персії, Китаю та Італії знали цей трикутник ще за кілька століть перед Паскалем.

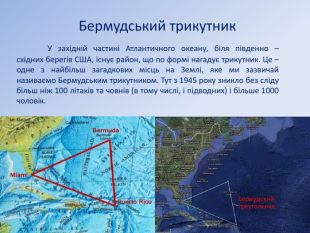
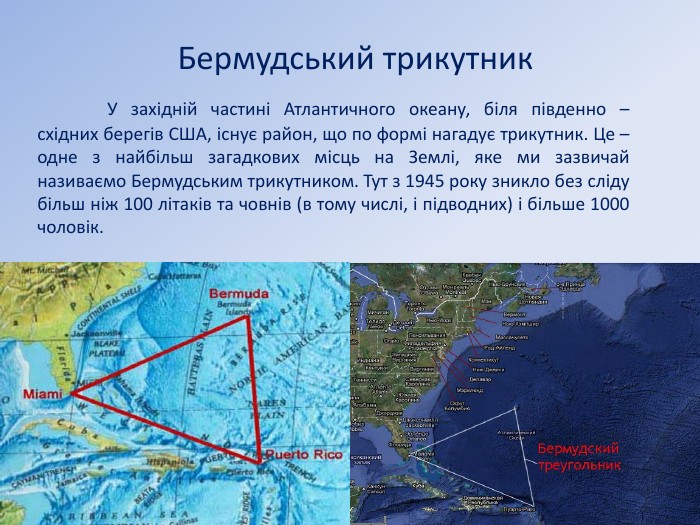
Бермудський трикутник У західній частині Атлантичного океану, біля південно – східних берегів США, існує район, що по формі нагадує трикутник. Це – одне з найбільш загадкових місць на Землі, яке ми зазвичай називаємо Бермудським трикутником. Тут з 1945 року зникло без сліду більш ніж 100 літаків та човнів (в тому числі, і підводних) і більше 1000 чоловік.

Трикутник (музичний інструмент) Трикутник — ударний музичний інструмент у вигляді зігнутого трикутником стального пруту (діаметр 8-10 мм), який вільно підвішують та вдаряють по ньому металевою паличкою. Звук трикутника — невизначеної висоти, дзвінкий, блискучий і в той же час ніжний. Розрізняють малий (довжина основи — 150 мм), середній (200 мм) та великий (250 мм). На трикутнику можна виконувати як окремі ритмічні удари, так і тремоло (швидке чергування ударами паличкою по сторонах трикутника). Походження трикутника достеменно невідомо, але зображення та описи музикознавців 16-17 ст. свідчать про те, що цей інструмент був відомий в Європі вже в ті часи. Початково трикутник пристосовувався переважно в воєнній музиці, пізніше (з кінця 19 ст.) — також і в симфонічній.

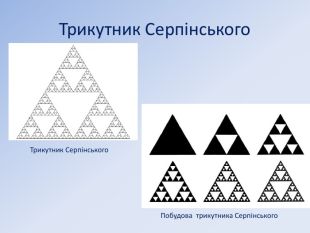
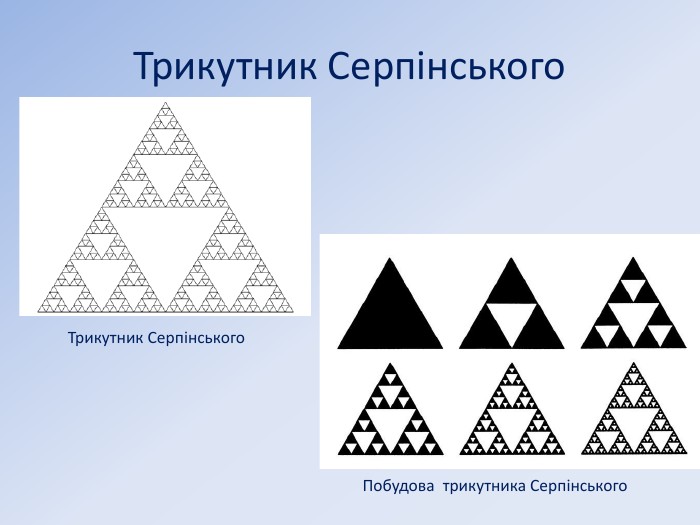
Трикутник Серпінського Трикутник Серпінського — фрактал, один із двовимірних аналогів множини Кантора, що був запропонований польським математиком Вацлавом Серпінським в 1915 році. Побудова. Береться рівносторонній трикутник. На першому кроці видаляється трикутник з вершинами в середині сторін початкового трикутника.Потым аналогічні трикутники із трьох менших трикутників, які залишилися після першого кроку, і т. д. Після нескінченного такого повторення, від суцільного трикутника залишається підмножина — трикутник Серпінського. Якщо в трикутнику Паскаля всі непарні числа пофарбувати в чорний колір, а парні - в білий, то утворюється трикутник Серпінського.

Трикутник Серпінського Трикутник Серпінського Побудова трикутника Серпінського

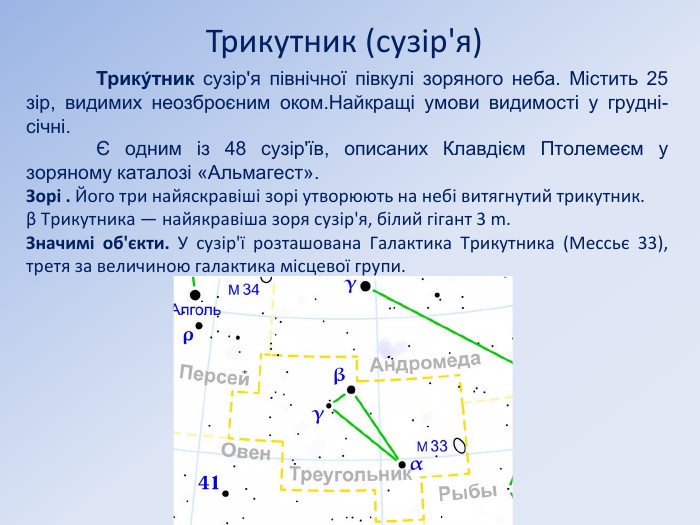
Трикутник (сузір'я) Трику́тник сузір'я північної півкулі зоряного неба. Містить 25 зір, видимих неозброєним оком.Найкращі умови видимості у грудні-січні. Є одним із 48 сузір'їв, описаних Клавдієм Птолемеєм у зоряному каталозі «Альмагест». Зорі . Його три найяскравіші зорі утворюють на небі витягнутий трикутник. β Трикутника — найякравіша зоря сузір'я, білий гігант 3 m. Значимі об'єкти. У сузір'ї розташована Галактика Трикутника (Мессьє 33), третя за величиною галактика місцевої групи.

Тадж-Махал — одне з головних визначних місць Індії. На Півночі Індії розкинулися три великих міста, в яких збереглася величезна кількість стародавніх пам'яток індійської культури. Ці міста, що приголомшують красою своїх храмів і мечетей, величчю фортів і розмахом усипальниць, з'єднані єдиним туристичним маршрутом під назвою «Золотий трикутник». Столична метушня Делі, чарівні легенди Агри і рожева пишність архітектури Джайпуру доповнюють один одного і дають туристові досить таки повне уявлення про історію, культуру та сучасний побут неймовірно загадкової Індії.

Трикутники в мистецтві

Трикутники в мистецтві Витинанки Витина́нки (від укр— «витинати» — «вирізувати») — вид давнього слов'янського, зок-рема українського народного декоративного мистецтва. Включає сюжетні та орнаментальні прикраси житла — ажурні, силуетні тощо. Виготовляється за допомогою ножиць, ножа, сокирки тощо знарядь. Матеріалом для витинанок є папір (білий або кольоровий), дерево, рослинні заготовки. Використовують витинанки для прикрашання приміщення (хати) — стін, вікон, полиць, коминів, печей. Витинанки застосовують як у побуті, так і перед релігійними чи світськими святами.

Трикутники в мистецтві

Трикутники в мистецтві

Трикутники в мистецтві

Дякую за увагу!