Презентація урок-дослідження "Симетрія у просторі та її властивості"

Симетрія у просторі та її властивостіКальченко Вікторія Іванівна. Урок геометріїу 10 класіКругляківської ЗОШІ-ІІІ ступенів

Перевірка домашнього завдання

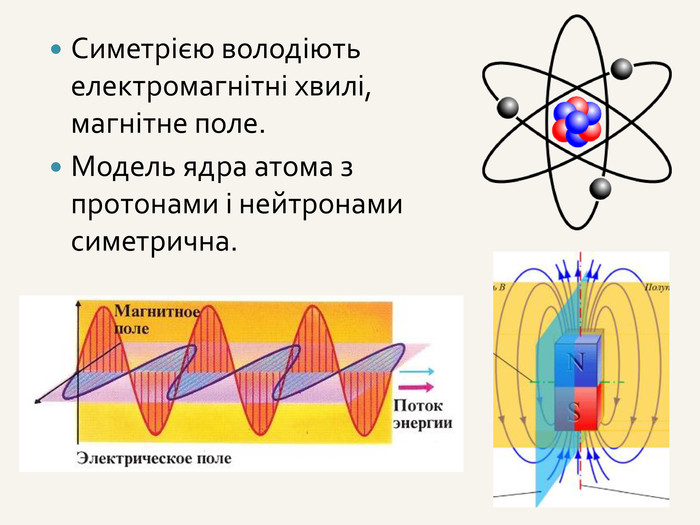
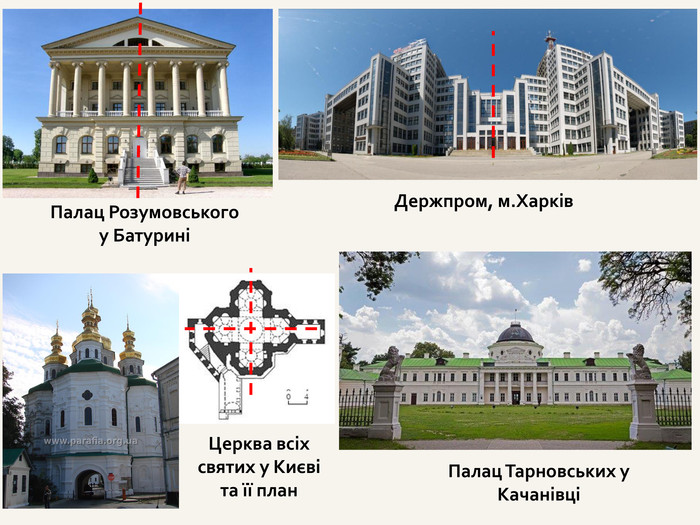
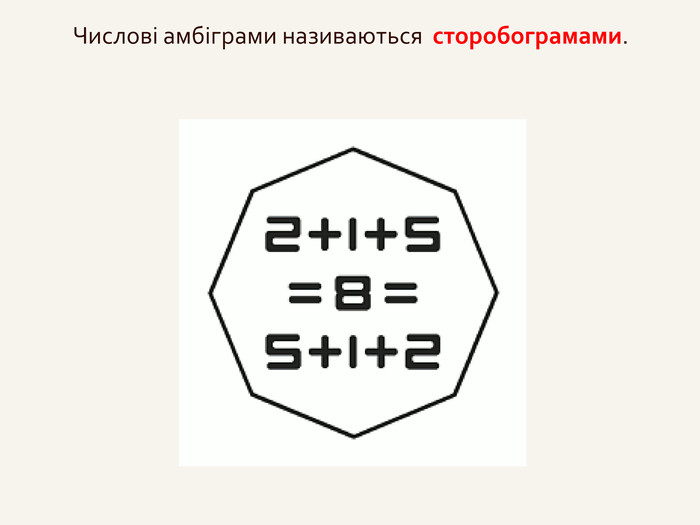
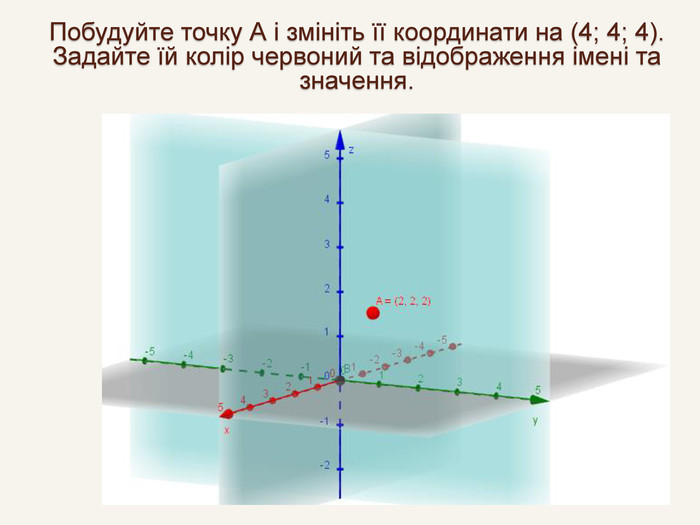
№ 1 Паралельне перенесення задано формулою:х' = х – 4; y ' = y + 2; z ' = z – 6.1) У яку точку перейде М(4; – 2; 7)? Розв’язання : М ' (4 – 4; – 2 + 2; 7 – 6), ( 0; 0; 1).2) Яка точка переходить у точку N ' (– 2; 0; – 1)? Розв’язання: – 2 = x – 4; x = 2, 0 = y + 2; y = – 2, – 1 = z – 6; z = 5. N ( 2; – 2 ; 5).

№ 2 При паралельному перенесенні точка М ( 2; – 3; 7) переходить у точку К (– 3; –5; 0). Складіть формули паралельного перенесення. Розв’язання : – 3 = 2 + а; а = – 5 , – 5 = – 3 + b; b = – 2, 0 = 7 + c; c = – 7 . х' = х – 5; y ' = y – 2; z ' = z – 7.

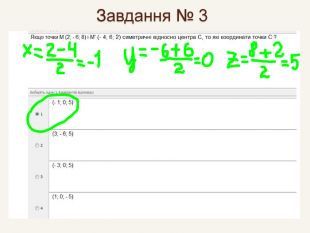
№ 3 Точка А (– 3; 1; – 6) А' (2; 3; – 9), точка В (4; – 6; 3) В' (9; – 4; 6). Чи існує таке паралельне перенесення? Розв’язання : Відповідні коефіцієнти с різні, отже це не є паралельним перенесенням.{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}для точок А і А' маємо: a = 5; b = 2; c = – 3. для точок B і B' маємо: a = 5; b = 2; c = 3.

Завдання уроку:

Завдання уроку: Поглибити знання про симетрію у просторі та її властивостіВизначити, чи зустрічається симетрія у навколишньому світіНавчитися використовувати властивості симетрії до розв’язування геометричних задач Навчитися будувати симетричні фігури

Актуалізація опорних знань“ПРАВДА чи БРЕХНЯ?”

Голосуйте картками:зелена – правда, червона - брехня1) Вісь Oz називається віссю аплікат.2) Правильний трикутник при переміщенні може перейти у прямокутний.3) Якщо точка А(8; 6 ; 3) В(5; 4 ; 0), а точка М(-1; 0; -1) К(- 4; - 2; 2), тоді це перетворення – паралельне перенесення 4) Якщо паралельне перенесення задано формулами x' = x – 2, y' = y + 1, z' = z + 2, тоді М (2; 3; – 4) К (0; 4; – 2) style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Вивчення нового матеріалу

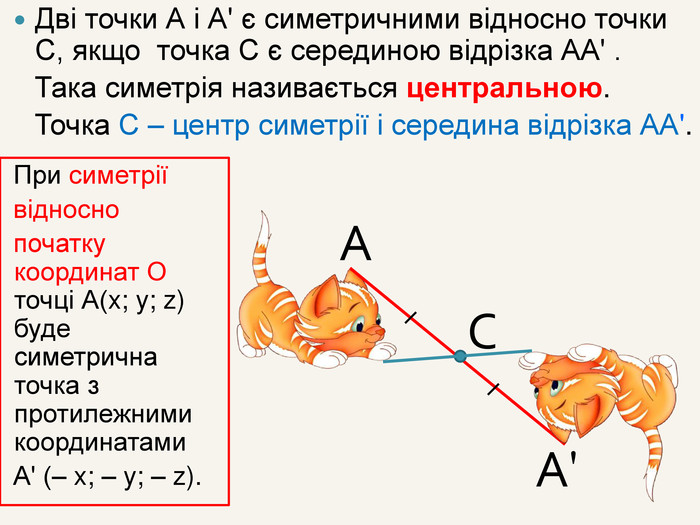
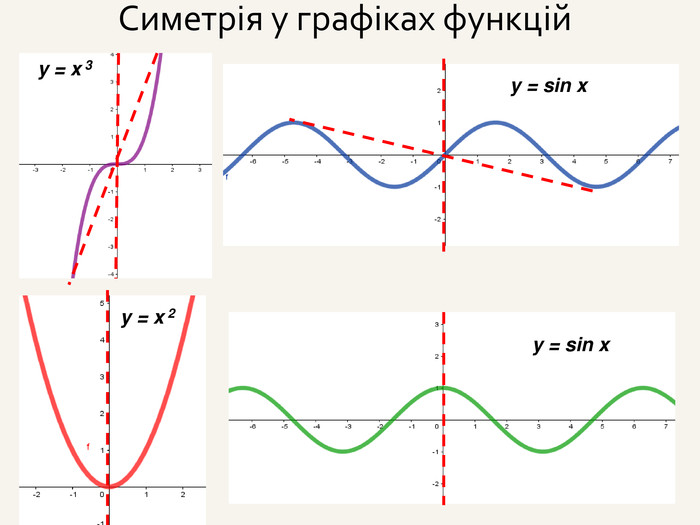
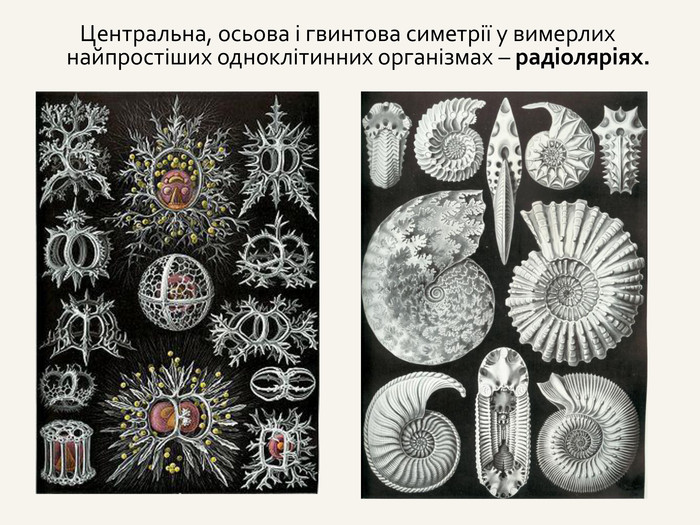
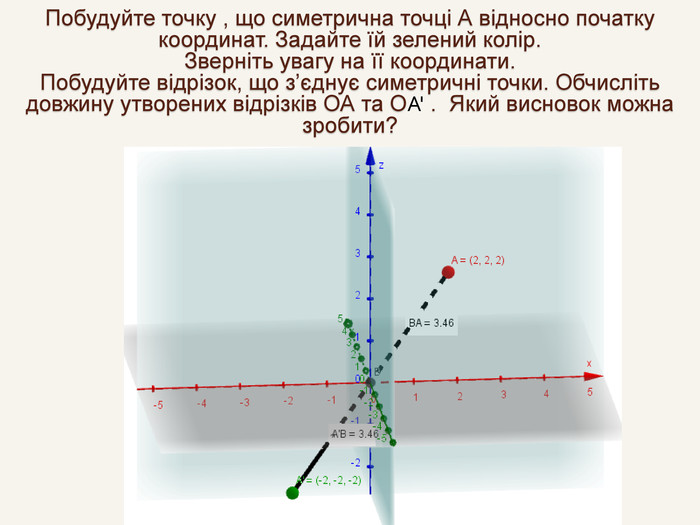
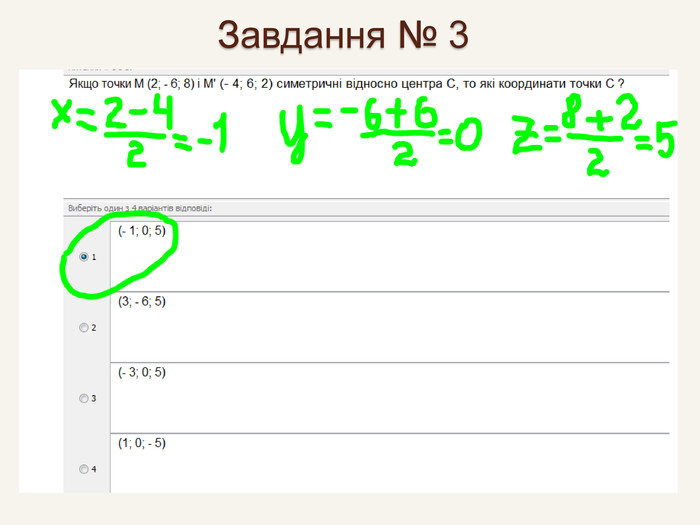
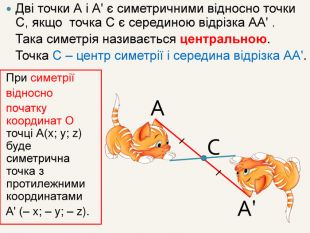
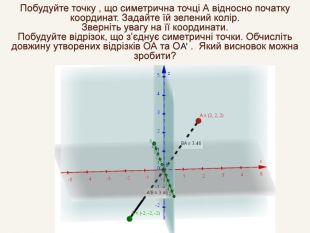
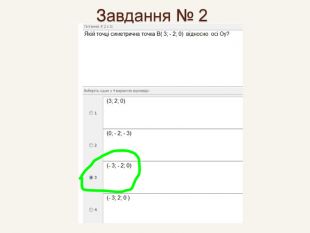
Дві точки А і А' є симетричними відносно точки С, якщо точка С є серединою відрізка АА' . Така симетрія називається центральною. Точка С – центр симетрії і середина відрізка АА'. САА'При симетрії відносно початку координат О точці А(x; y; z) буде симетрична точка з протилежними координатами. А' (– x; – y; – z).

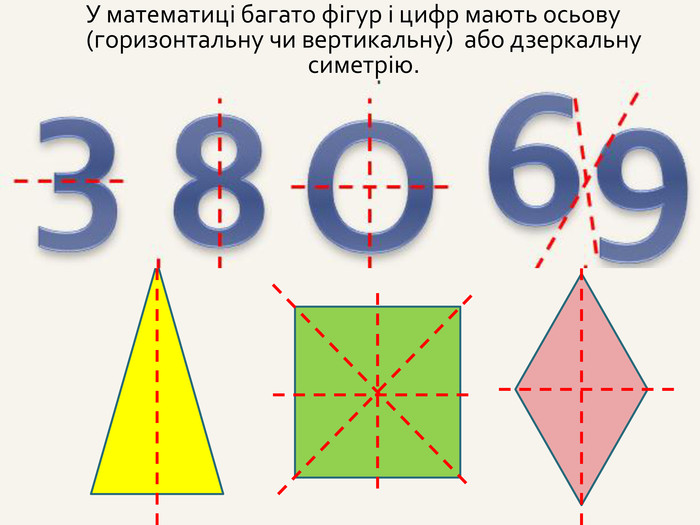
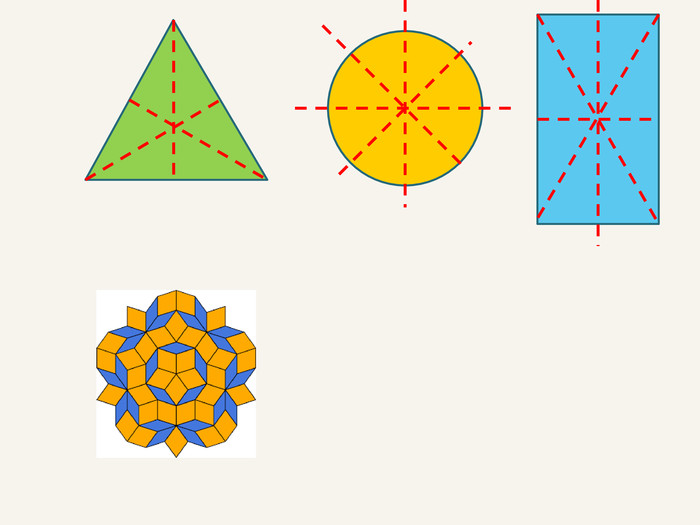
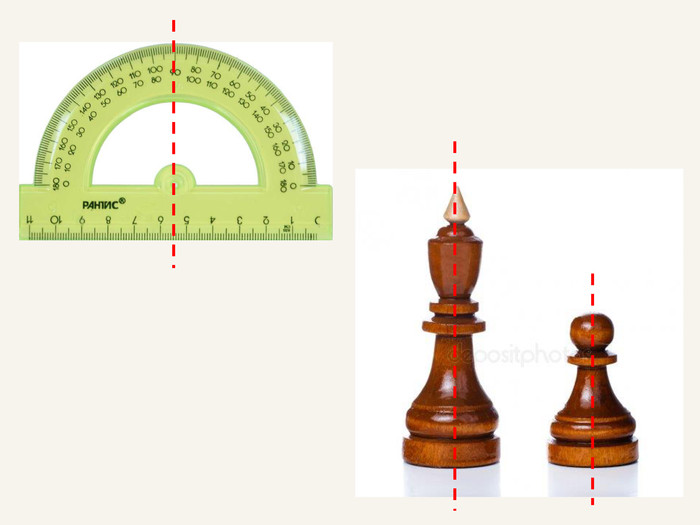
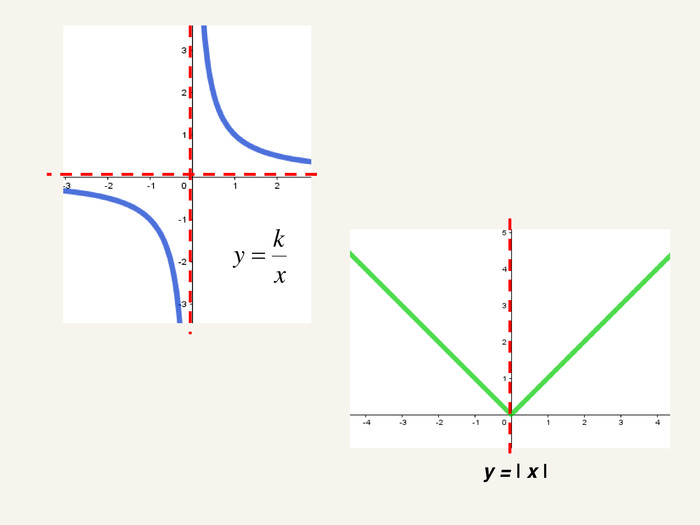
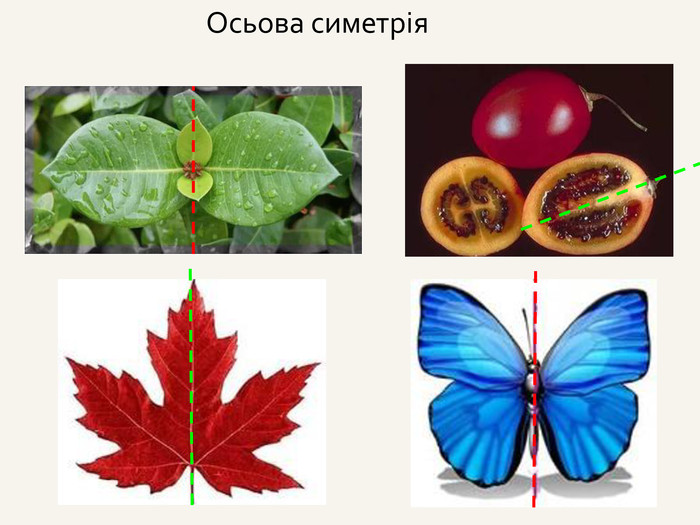
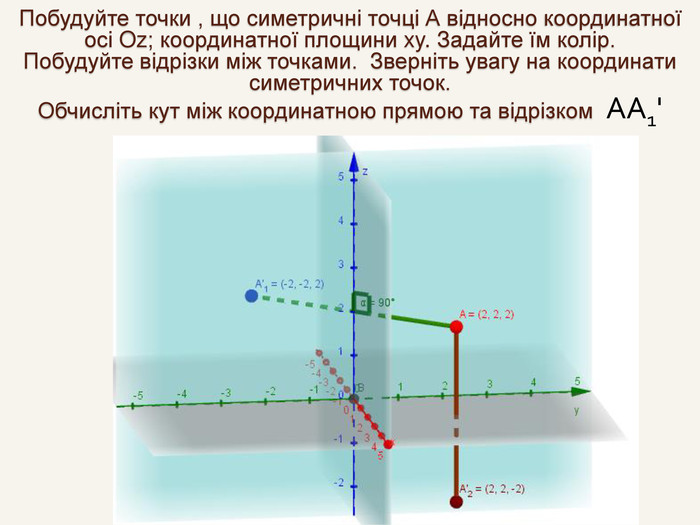
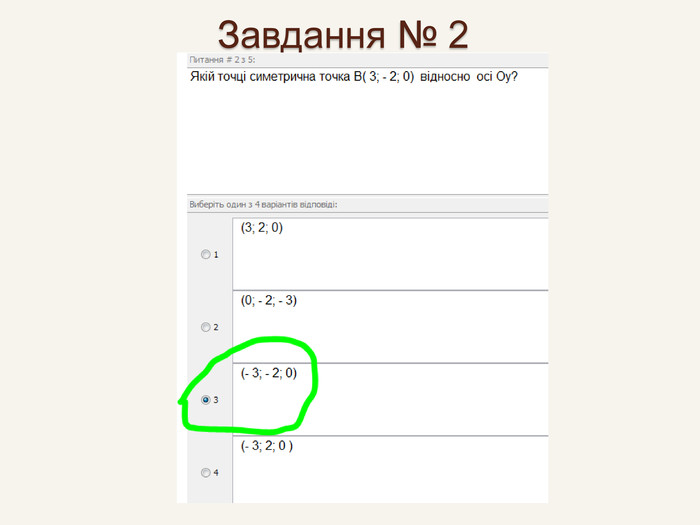
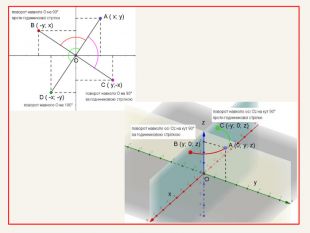
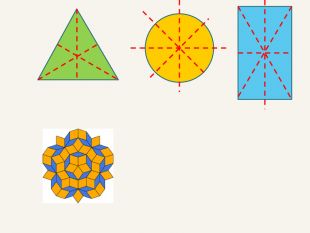
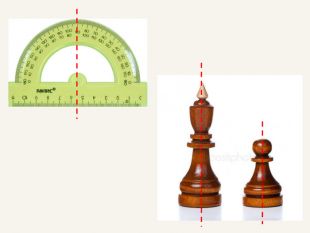
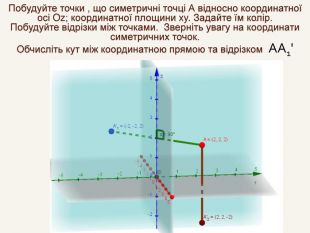
Дві точки А і А' є симетричними відносно прямої m, якщо пряма m є серединним перпендикуляром до відрізка АА' . Така симетрія називається осьовою. Пряма m – вісь симетрії.m. АА'При симетрії відносно координатної осі точці А(x; y; z) буде симетрична така точка А', у якої відповідна даній осі координата буде без зміни, а інші координатибудуть протилежнимичислами.

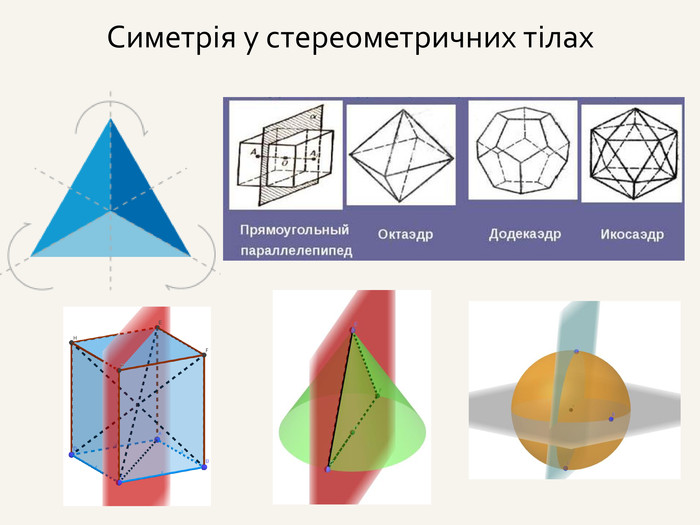
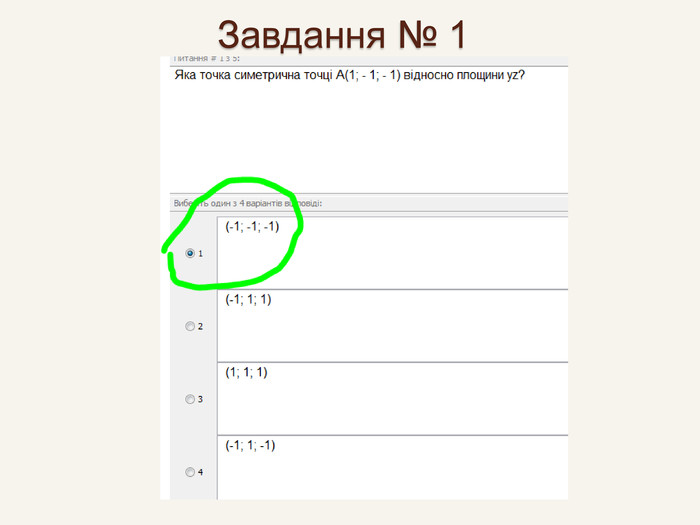
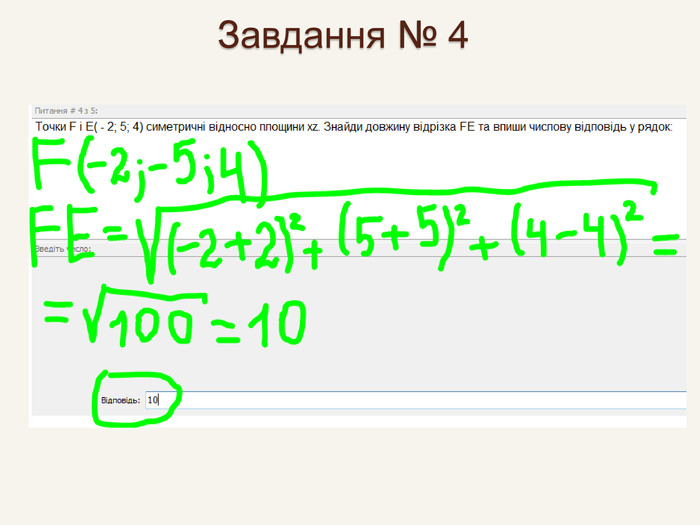
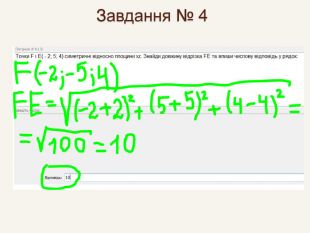
Дві точки А і А' є симетричними відносно площини β, якщо ця площина є перпендикулярною до відрізка АА' і ділить його навпіл. Така симетрія називається дзеркальною. Площина β – площина симетрії.βА'А{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}При симетрії відносно координатної площини точці А(x; y; z) буде симетрична така точка, у якої відповідні даній площині координати будутьбез зміни, а інша – з протилежним знаком.

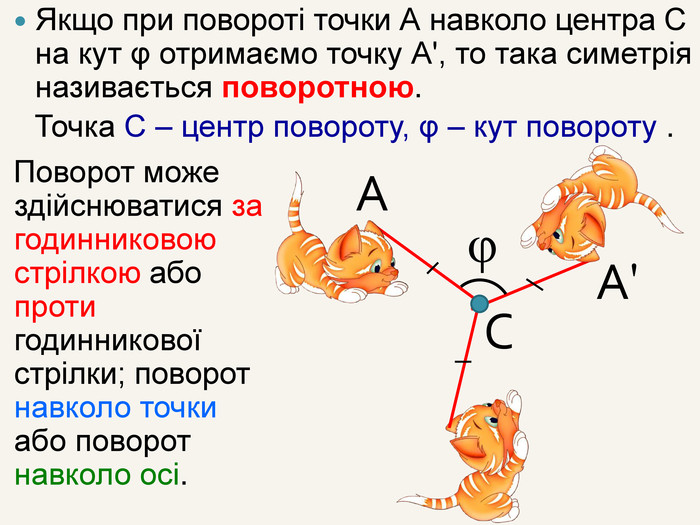
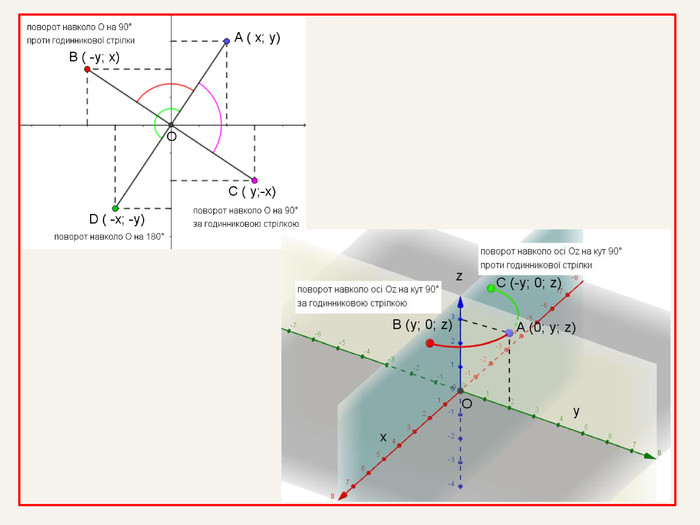
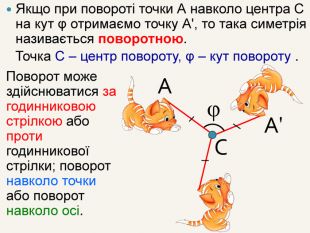
Якщо при повороті точки А навколо центра С на кут φ отримаємо точку А', то така симетрія називається поворотною. Точка С – центр повороту, φ – кут повороту . САА'φПоворот може здійснюватися за годинниковою стрілкою або проти годинникової стрілки; поворот навколо точки або поворот навколо осі.

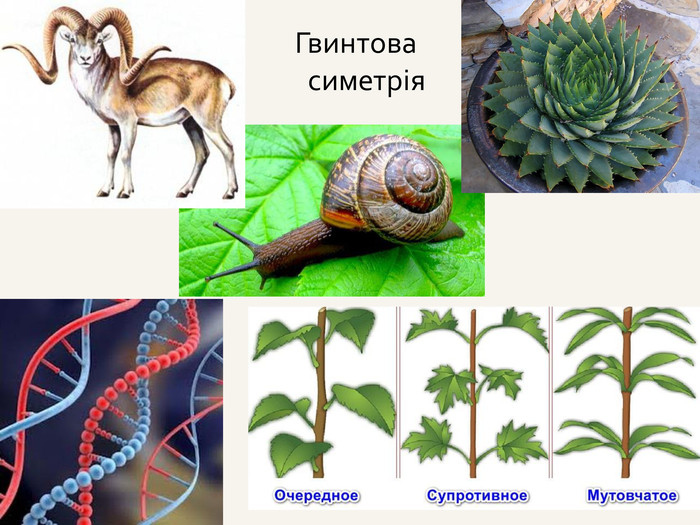
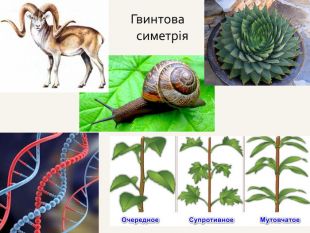
Якщо точка А здійснює перенесення вздовж осі, доповнене обертанням навколо неї на кут 90°, то така симетрія називається гвинтовою. Переносна та гвинтова симетрії є нетрадиційними видами симетрії . Поворот на кут 180° є центральною симетрією. Поворот на кут 90° є осьовою симетрією. Якщо при повороті фігура переходить сама у себе, то це – переносна симетрія.

Проект учнів 10 класу“Симетрія у навколишньому світі”

Симетрія у математиці

У математиці багато фігур і цифр мають осьову (горизонтальну чи вертикальну) або дзеркальну симетрію.

Симетрія у стереометричних тілах

Симетрія у графіках функційy = sin x y = sin x y = x 3y = x 2

y = ǀ x ǀ

Симетрія у біології

У живій і неживій природі симетрія зустрічається дуже часто. Це зумовлено способом існування – несиметричні комахи і птахи не змогли б літати, листочки у рослинах затіняли б одне одного. Центральна і поворотна симетріїАденовірус. Медуза

Осьова симетрія

Дзеркальна симетрія

Гвинтова симетрія

Центральна, осьова і гвинтова симетрії у вимерлих найпростіших одноклітинних організмах – радіоляріях.

Скелет людини теж побудований за принципом симетрії, адже несиметричний опорний апарат втратив би свою нормальну функціональність.

Симетрія у хімії

Більшість простих молекул та кристалічних решіток мають симетрію, що проявляється у фізичних та хімічних властивостях речовин. Кристалічна решітка натрію хлориду(кухонної солі)Кристалічна решітка броміду срібла

Симетрія многогранників яскраво проявляється у структурі мінералів

Молекула води володіє симетрією. Симетричні кристалічні решітки льоду та снігу. Симетричні також і сніжинки.

Симетрія у фізиці і техніці

Жоден з технічних засобів – від шестерні до ракети – не працював би без симетрії!

Симетрією володіють електромагнітні хвилі, магнітне поле. Модель ядра атома з протонами і нейтронами симетрична.

Галактики і квазари мають симетричну будову. Магнітне поле Землі теж симетричне відносно полюсів. Галактика Молочний шлях. Найстаріша галактика А1689 В11. Їй 2,6 млдр.років. Квазари

Симетрія в архітектурі

Вибираючи симетричні форми, архітектори прагнули досягти природної гармонії , як ознаки стійкості та рівноваги. Тадж-Махал, Індія. Собор Паризької БогоматеріПантеон

Храм Лотоса в ІндіїБашти Петронаса у МалайзіїЕйфелева вежа у Парижі, Франція

Приклад використання симетрії у садово-парковому мистецтві – топіарії.

Церква всіх святих у Києві та її план. Палац Розумовського у БатуриніДержпром, м. Харків. Палац Тарновських у Качанівці

Симетрія у мистецтві і побуті

Щодня у побуті ми стикаємося з проявами симетрії. Без симетрії не стояв би стілець, не трималися б окуляри, гвинт неможливо було б вкрутити.

Килими, мереживо, витинанки, розписи на стінах та декоративному посуді, прикраси – це теж прояв досконалості через симетрію.

Симетрія в українській вишивці

Симетрія в філології

Симетрія літер

Амбіграма (від лат. ambi — «подвійний», і грец. gramma — «буква») — каліграфічний візерунок, що дозволяє поєднати два різні прочитання з одного і того ж набору ліній.

Числові амбіграми називаються сторобограмами.

Літературним праобразом амбіграм можна вважати паліндроми — слова або фрази, які читаються однаково як зліва направо, так і справа наліво.

Симетрія у історії

Пізнавальну силу симетрії оцінили філософи Стародавньої Греції, використовуючи її в своїх теоріях. Так, наприкфілософськихлад, Анаксимандр з Мілета, який жив у першій половині VI ст. до н. е., використовував симетрію в своїй космологічної теорії, де в центрі світу помістив Землю - головне, на його думку, тіло світу. Вона повинна була мати досконалу, симетричну форму, форму циліндра, а на периферії обертаються величезні вогняні кільця, закриті повітряними хмарами і дірками, які і здаються нам зірками. Земля розташована точно в центрі, і тут симетрія має сенс рівноваги.

Емпедокл вважав Всесвіт сферою - втіленням гармонії і спокою. Сферос - величезний однорідний шар, породження двох протилежних стихій - Любові і ворожнечі. Перша стихія з'єднує, друга - роз'єднує. Їх гармонія - симетрія - призводить до стійкого, циклічного рівноваги світу - Сферос. Переважання однієї чи іншої стихією - асиметрія - призводить до циклічного ходу світового процесу.

Ідею симетрії використовували Левкіпп і Демокріт. За їх вченням, світ складається з порожнечі і атомів, з яких побудовані всі тіла і душі. Таким чином, стародавнє мистецтво використовувало просторову симетрію. Гармонія (симетрія) складається з протилежностей. В просторової симетрії протилежності явно видно. Наприклад, права і ліва кисті рук людини. Таких протилежностей стародавні вчені нарахували десять пар, наприклад, парне - непарне, пряме - криве, праве - ліве і т.д. Левкіпп. Демокріт

Леонардо да Вінчі не оминув своєю увагою і симетрію. Він розглянув рівновагу кулі, що має опору в центрі ваги: дві симетричні половини кулі врівноважують одна одну, і куля не падає. Як художник він головну увагу приділяв вивченню законів перспективи і пропорцій, за допомогою яких виявляються художні достоїнства творів мистецтва.

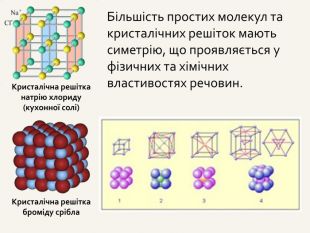
У науку симетрія увійшла в 30-х рр. XIX ст. в зв'язку з відкриттям Гесселем 32 кристалографічних класів і появою теорії груп як області чистої математики. Кристали наділені найбільшою величиною симетрії з усіх реальних об'єктів, вони блищать своєю симетрією. Кристали - це симетричні тіла, структура яких визначається періодичним повторенням в трьох вимірах елементарного атомного мотиву.

Е. Галуа запропонував класифікувати алгебраїчні рівняння за їх групами симетрії.

Ф. Клейн запропонував взяти ідею симетрії як єдиного принципу при побудові різних геометрій. Клейн розвинув свою концепцію у фізиці і механіці. Програма Клейна як завдання пошуку різних форм симетрії виходить за рамки не тільки геометрії, але і всієї математики в цілому, перетворюється в проблему пошуку єдиного принципу для всього природознавства.

Знання збираються по краплині, як вода в долиніУкраїнське прислів’я

Закріплення нового матеріалу

Групова робота із завданнями

№ 1 Запишіть координати точок, симетричних точці А (3;– 4; 1) відносно:1) Початку координат (– 3; 4; – 1) 2) Площини xy 3) Площини xz 4) Осі Oz ( 3;– 4; – 1) ( 3; 4; 1) (– 3; 4; 1)

№ 2 Точки А (5;– 3; 4) та В (– 3; 1; – 2) симетричні відносно точки С. Які її координати?Розв’язання: За означенням центральної симетрії точка С – середина відрізка АВ. Тоді: xc = = 1; уc = = –1; zc = = 1; Відповідь: С ( 1;– 1; 1)

№ 3 Точки E (– 3; 8; 7) та F симетричні відносно площини ху. Знайдіть довжину відрізка EF. Розв’язання: За властивістю дзеркальної симетрії будуть такі координати точки F : (– 3; 8; –7). Тоді за формулою довжини відрізка маємо: EF = = = Відповідь: EF = 14.

Робота у динамічному середовищі

Побудуйте точку А і змініть її координати на (4; 4; 4). Задайте їй колір червоний та відображення імені та значення.

Побудуйте точку , що симетрична точці А відносно початку координат. Задайте їй зелений колір. Зверніть увагу на її координати. Побудуйте відрізок, що з’єднує симетричні точки. Обчисліть довжину утворених відрізків ОА та ОА' . Який висновок можна зробити?

Побудуйте точки , що симетричні точці А відносно координатної осі Oz; координатної площини xy. Задайте їм колір. Побудуйте відрізки між точками. Зверніть увагу на координати симетричних точок. Обчисліть кут між координатною прямою та відрізком АА1'

Самостійна робота

Відкрийте на робочому столі файл САМОСТІЙНА РОБОТА програми Мій. Тест, зареєструйтеся та виконайте завдання самостійної роботи

Завдання № 1

Завдання № 2

Завдання № 3

Завдання № 4

Завдання № 5

Домашнє завдання. Блог вчителя математики Кальченко Вікторії Іванівниhttps://sites.google.com/site/kalchenkovi78/Домашнє завдання 10 клас Симетрія.docx

Підсумки уроку

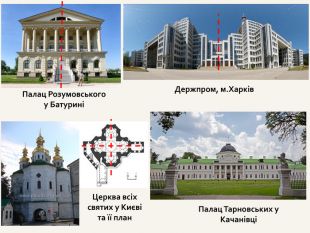
Визначення досягнутих завдань {8799 B23 B-EC83-4686-B30 A-512413 B5 E67 A}Поглибити знання про симетрію у просторі та її властивостіВизначити, чи зустрічається симетрія у навколишньому світіНавчитися використовувати властивості симетрії до розв’язування геометричних задач Навчитися будувати симетричні фігури. Вияснити, чи міг би наш світ існувати без симетрії повноцінно?

СИМЕТРІЯЦЕНТРАЛЬНАОСЬОВАДЗЕРКАЛЬНАГВИНТОВАПЕРЕНОСНА

Рефлексія

Встановіть цеглинку відповідного кольору у піраміду на ту висоту, на якій тепер знаходяться ваші знання. Зелену – задоволений, Червону – не задоволений

Урок закінчено!Бажаю успіху у здобутті нових знань!