ТЕСТ «Рівнобедрений трикутник та його властивості»

ТЕСТ                                                                                                                                  «Рівнобедрений трикутник та його властивості»

1.Рівнобедрений трикутник – це трикутник, у якого ….

а) всі сторони різні;

б) всі сторони рівні;

в) дві сторони рівні.

2.Які існують види трикутників в залежності від кількості рівних сторін?

а) прямокутний, гострокутний, тупокутний;

б) рівносторонній, нерівносторонній;

в) рівнобедрений, рівносторонній, різносторонній.

3.Яку сторону рівнобедреного трикутника називають основою?

а) рівні;

б) третю сторону;

в) ту, на якій стоїть трикутник.

4. Яку сторону рівнобедреного трикутника називають бічною?

а) рівні;

б) третю сторону;

в) ту, на якій стоїть трикутник.

5.Властивості кутів рівнобедреного трикутника:

а) кути при основі рівні;

б) проти рівних сторін лежать рівні кути;

в) бісектриса трикутника, проведена із кута при вершині, є і медіаною, і висотою.

6.Знайти периметр рівнобедреного трикутника, основа якого дорівнює 10 см , а бічна сторона – 7см.

а) 27см;

б) 24см;

в) 17см.

7.Знайти сторони рівнобедреного трикутника, периметр якого дорівнює 28см, а основа на 4см більше, ніж бічна сторона.

а) 4; 8; 12 см;

б) 12; 12; 4 см;

в) 8;  8; 12 см.

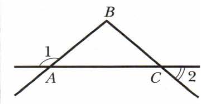
8.На малюнку АВ=ВС, ﮮ 1=130º. Знайти  ﮮ 2.

а) 130º ;

б) 50º ;

в) 55º .

9.Одна із сторін рівнобедреного трикутника дорівнює 5см. Знайти дві інші сторони, якщо периметр трикутника дорівнює 25 см.

а) 5см і 15 см;

б) 10см і 10см;

в) 10см і 5см.