Презентація "Урок однієї задачі"
Про матеріал
Урок комплексного застосування знань, умінь, навичок учнів.
Метою уроку є:
- систематизація набутих знань про трикутник та коло;
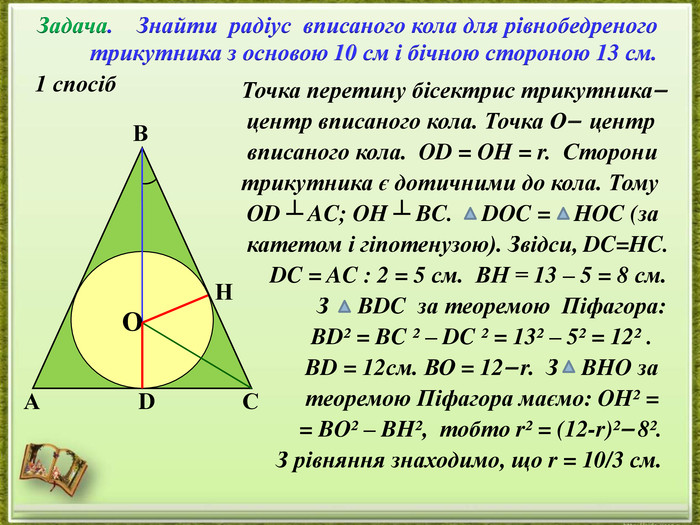
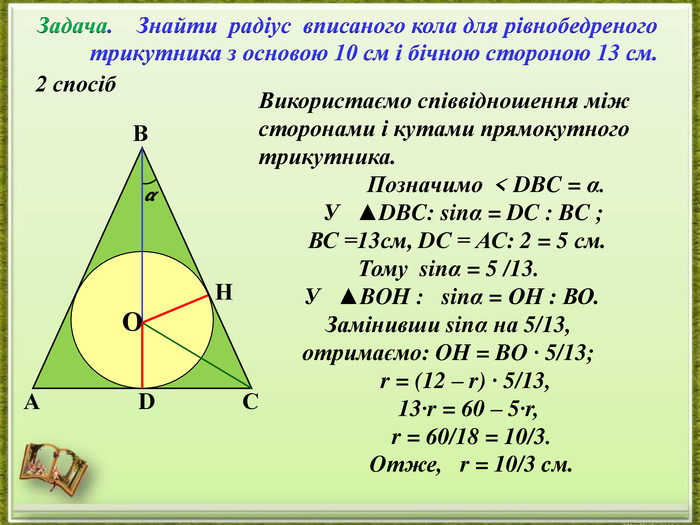
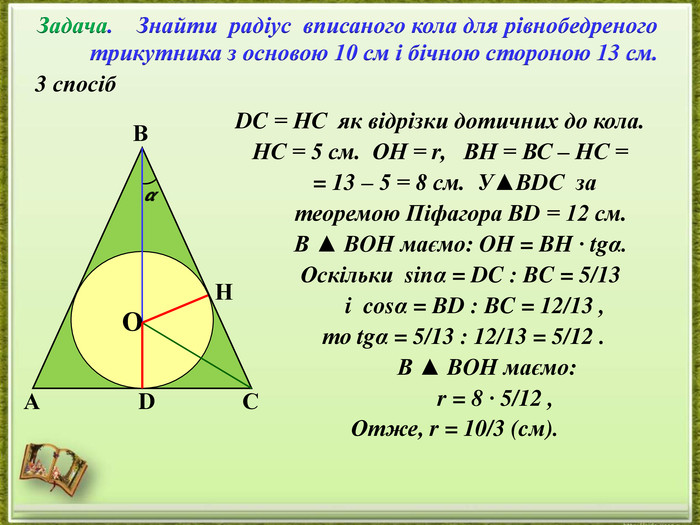
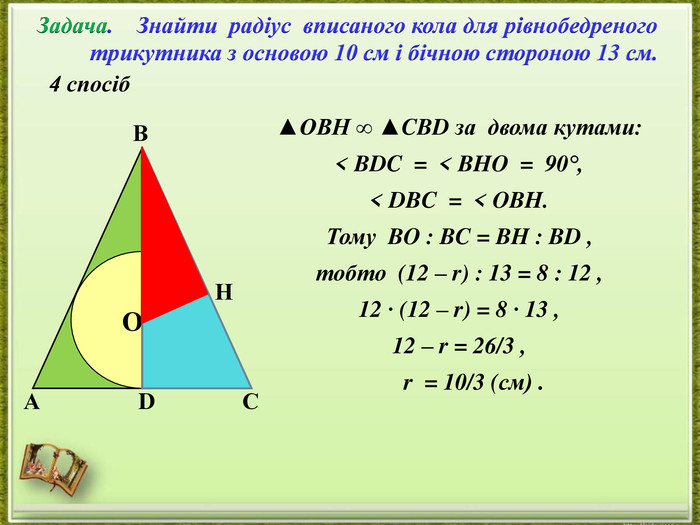
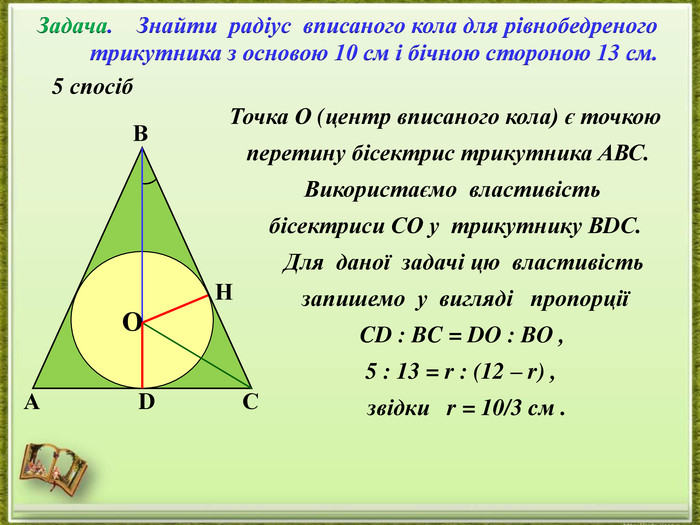
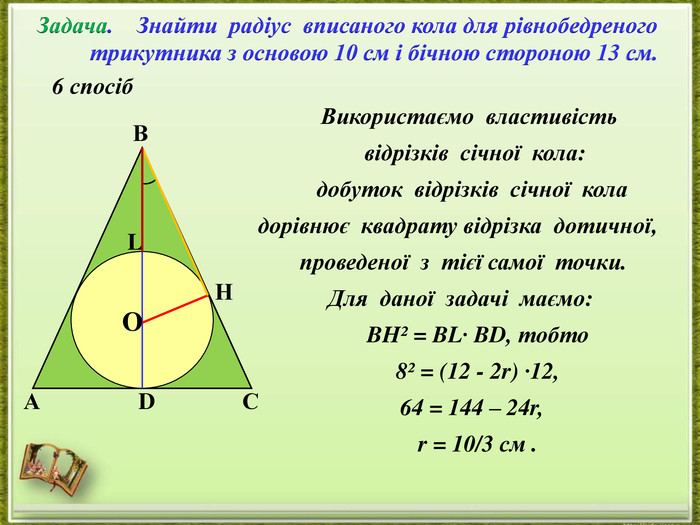
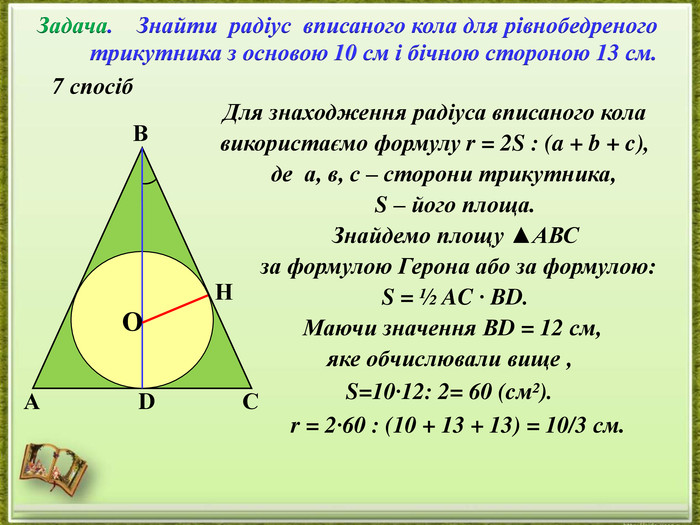
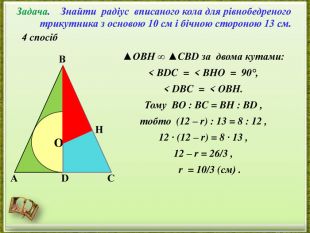
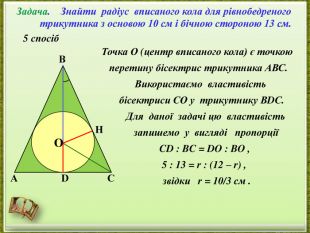
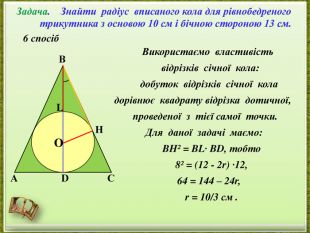
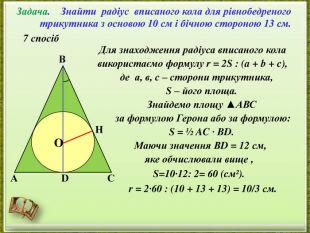
- представлення дослідження різних способів розв’язання однієї задачі;
- демонстрація творчого застосування вмінь і навичок з різних тем планіметрії.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку