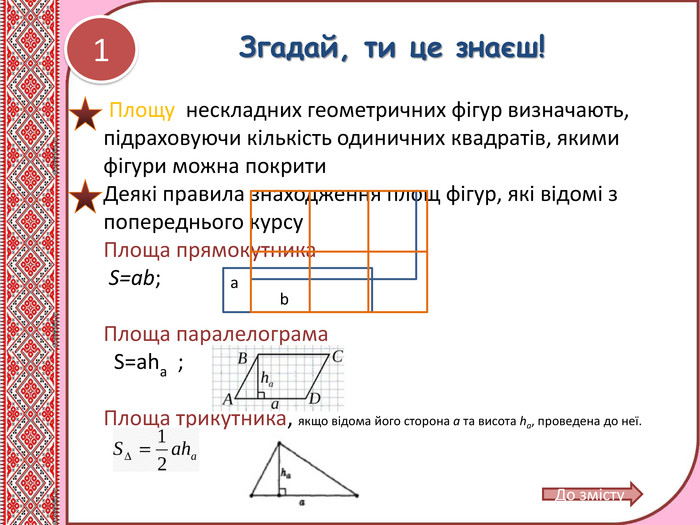
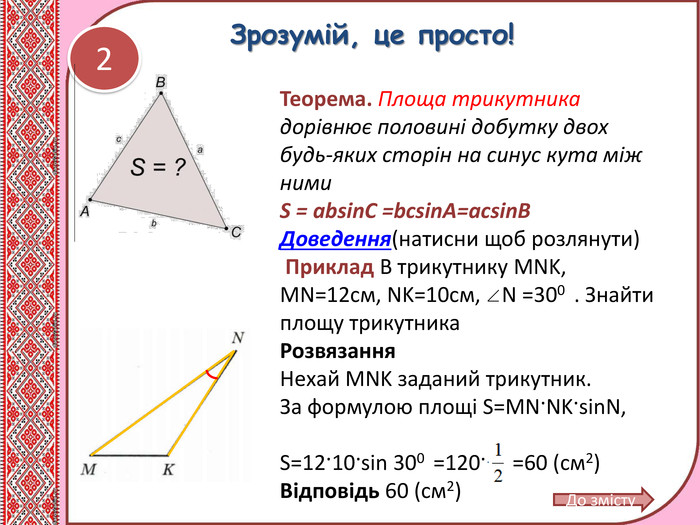
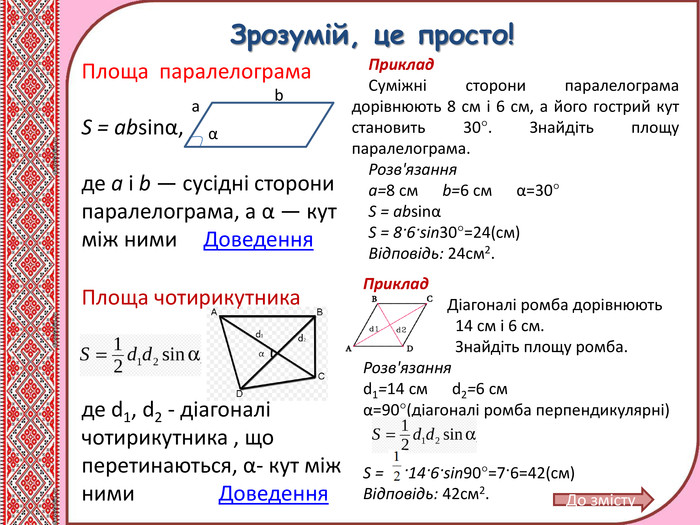
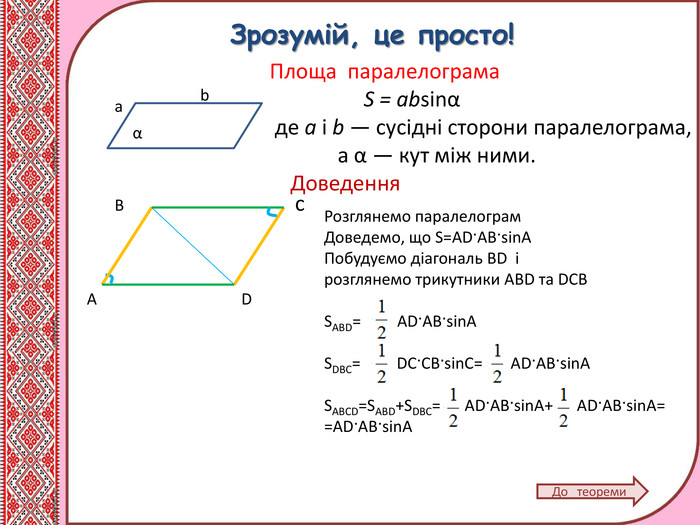
Презентація. Урок. "Площі трикутника і чотирикутника"
Про матеріал
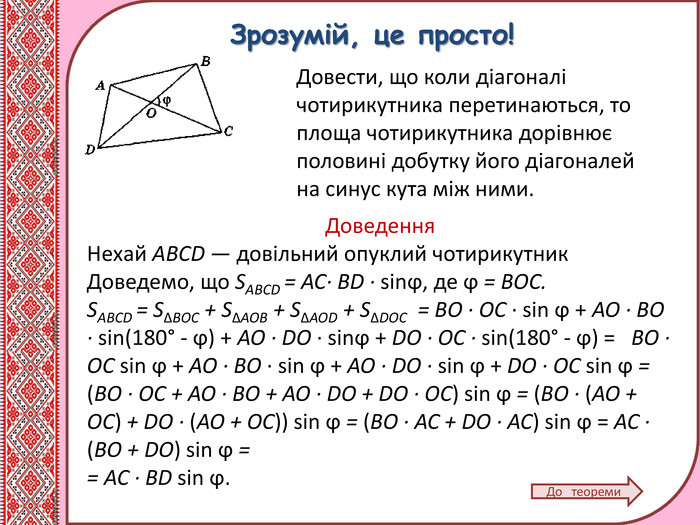
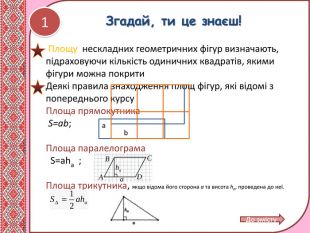
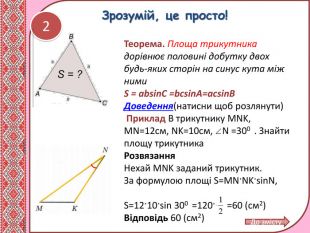
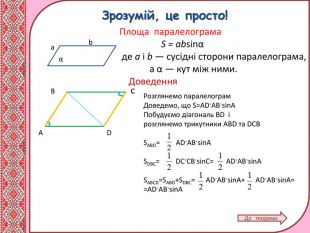
Матеріал містить теоретичний матеріал з теми "Площі трикутника і чотирикутника,", розв'язання типових задач, вправи для самоконтролю. Може використовуватись при дтстанційному навчанні учнів. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку