Тема "Вектори на площині"

Тема. Узагальнення і систематизація знань з теми «Вектори на площині»

Навчальна мета: визначити рівень знань засвоєння навчального матеріалу з теми «Вектори» згідно діючої програми навчання математики;

систематизувати уявлення про основні поняття із вказаної теми;

узагальнити набуті знання і навички та провести широку систематизацію (перенесення набутих умінь і навичок і застосування отриманих знань у навчальному процесі та власному повсякденному житті); формування вмінь і знань створення проекту.

Розвивальна мета: розвивати мислення та дослідницькі навики учнів;

розвивати вміння прогнозувати, здійснювати пошук та ліквідувати помилки у відповідях товаришів; сприяти формуванню цілісної інформаційної картини (встановлення причинно-наслідкових зв’язків).

Виховна мета: формувати культуру оформлення результатів дослідження даних; розвиток умінь робити висновки та приймати самостійні рішення;

формування само оцінювання;  виховання в учнів відчуття колективізму та вміння поєднувати індивідуальну роботу з колективною.

Тим уроку: узагальнення та систематизація знань.

Хід уроку

І. Організаційний момент

 Привітання, перевірка наявності учнів, готовності їх до уроку.

 

Доброго дня! Сідайте. Як ваш настрій? Чи настроєні ви на роботу?

Подивіться один на одного і посміхніться! Починаємо урок!

У вас на партах лежать картки з зображенням емоцій. Виберіть і піднесіть вгору ту картку, яка відповідає вашому емоційному стану на даний момент.

 

Вчитель:Тема уроку: «Вектори».

Метою нашого сьогоднішнього уроку є: систематизація знань,умінь і навичок з даної теми.

 На уроці ми з вами повторимо теорію, проведемо усну роботу, розглянемо розв’язування задач.

Епіграф уроку:

Не просто слухати, а чути.

Не просто дивитися, а бачити.

Не просто відповідати, а міркувати.

Дружно і плідно працювати

 

ІІ. Перевірка домашнього завдання

ІІІ. Актуалізація опорних знань

Оцінювання учнями власних знань та роботи у групі (класі)

Для оцінювання учнями власної участі у роботі роздані анкети.

Прізвище, ім’я _____________________

(Оцініть себе по кожному з визначених напрямків від 0 до 2 балів)

Ви брали активну участь у роботі групи ___________

Ви вносили вдалі пропозиції, які врахувала група __________

Ви добре володієте матеріалом з даної теми _______

Ви висували цілком нову ідею, що сподобалась іншим _____________

Ви вдало узагальнювали думки інших і просували групу вперед____________

Ви працювали над проектом_____________

Всього балів _________

Бали за результатами тестування ____________

 

Гра «Математичне доміно»

(готується набір карток двох кольорів. На одних записується початок речення, на інших його закінчення )

Наприклад:

Початок речення	Закінчення речення
Вектори називаються рівними …	Якщо вони співнапрямлені і мають рівні довжини
Два ненульових вектори називаються колінеарними…..	Якщо вони паралельні одній прямій
Щоб задати вектор…	Достатньо вказати його початок і кінець.
Два вектори називають протилежними векторами….	Якщо вони мають рівні модулі, але протилежні напрями.
Співнапрямленими векторами називають колінеарні вектори…	Якщо вони мають однаковий напрямок.
Нуль-вектором називають вектор…	Якщо його початок і кінець співпадають.
Довжиною вектора називають…	Відстань між його початком і кінцем.
Довжина нуль-вектора….	Дорівнює нулю.
Довжина і напрям вектора не залежать від…	Розміщення його початку в системі координат
Вектори рівні…	Коли їх відповідні координати рівні.
Вектори колінеарні…	Коли їх відповідні координати пропорційні

 

( Кожній групі учнів роздається доміно, яке необхідно скласти у відповідності:  початок речення – кінець )

 

Розв’язування задач усно

Вчитель: Давайте пограємо в гру «Вірю - не вірю»

1) Одиничний вектор має координати (1;1). –

(Одиничним вектором (ортом) називається вектор с, довжина якого дорівнює 1: = 1)

2) Вектори AB, BA рівні. –

(Вектори і називаються рівними, якщо вони мають одна­кову довжину та однаково напрямлені)

3) Протилежно напрямлені вектори колінеарні. +

(Ненульові вектори називаються колінеарними, якщо вони ле­жать або на одній прямій, або на паралельних прямих)

4) Нульовий вектор колінеарний будь-якому вектору. +

(нульовий вектор вважається колінеарним будь-якому вектору.)

5)Якщо два ненульові вектори взаємно перпен­дикулярні,то скалярний добуток дорівнює нулю +

(Два ненульові вектори тоді і тільки тоді взаємно перпен­дикулярні, коли їх скалярний добуток дорівнює нулю)

Розв'язування вправ

1. Дано точки А(2; 3), B(1; 1). Які координати мають вектори і ?
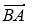2. Знайдіть координати вектора , якщо А(5; 1) і О — поча­ток координат.
3. Знайдіть 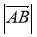, якщо А(1; 2), В(-3; -2).
4. Дано точки: А(3; -2), В(-4; 6), С(-2; -6), D(x; y). Знай­діть х і у, якщо =  .

 

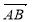Колективне виконання вправ

1. Серед векторів (-2; 4), 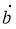(2; 2), 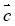(0; -1), 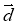(1; -2) знайдіть колінеарні.

Розв'язування

Оскільки вектори колінеарні, якщо їхні відповідні коорди­нати пропорційні, то маємо  = -2, звідси вектори i колінеарні.

Відповідь: i .

2. Знайдіть довжину вектора (6; у), якщо він колінеарний век­тору 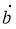+ 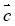, де 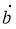(-2; 0), 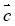(0; 1).

Розв'язання

Нехай + = , тоді (-2 + 0; 0 + 1) = (-2; 1). Оскільки векто­ри і колінеарні, то , звідси у = = -3, тоді (6; -3) і = =       = = = = 3.

Відповідь: 3

 

Перевірка знань у вигляді тестів

Варіант 1

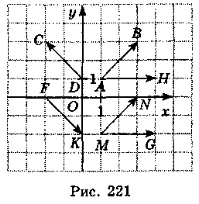
Користуючись рис. 221, виконайте завдання 1—6.

I рівень

1. Знайдіть координати вектора .
   А (1; 1) Б (-2; 2) В (2; 2) Г (2; -2)
2. Укажіть координати вектора -.

А (-2; 2) Б (2; -2);   В (2; 2) Г (-2; -2)

3. Укажіть вектор, який дорівнює век­тору .

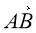A  Б  В  Г

II рівень

4. Укажіть координати вектора + .

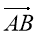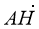А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)

5. Укажіть координати вектора – .

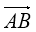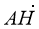А (1; 2) Б (-1; 2) В (1; -2)  Г(-1; -2)

6. Знайдіть ∙ .

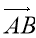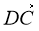А   Б 2  В 0   Г 1

ІІІ рівень

7. При якому значенні вектори (1; -1) і 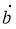(п; 1) колінеарні?

А Ні при яких п   Б п = -1 

В п = 1   Г п = ±1

8. При якому значенні п вектори (1; 1) і 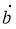(п; 1) перпендику­лярні?

А п = 1   Б п = -1 

В п = ±1    Г ні при яких п

9. Знайдіть координати вершини D паралелограма ABCD, якщо А(0; 2),    В(1; 0), С(2; 0).

А D(1; 2) Б D(2; 2) В D(1; -2)  Г D(2; 1)

IV рівень

10. Дано точки A(2; 1), B(3; 2), C(3; 1). Знайдіть внутрішній кут С трикутника ABC.

А 30°  Б 45°  В 60°  Г 90°

11. Знайдіть площу чотирикутника ABCD, якщо А(0; 1), В(1; 3), С(2; 1),     D(1; -1).

А 2  Б 4  В 6  Г 8

12. Знайдіть кут А трикутника ABC, якщо А(0; 1), В(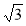; 2), С(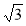; 1).

А 30°  Б 45°  В 60°  Г 90°

 

Варіант 2

Користуючись рис. 222, виконайте завдання 1—6.

I рівень

1. Знайдіть координати вектора .
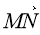   А(1; 1) Б (-2; 2) В (2; 2) Г(2; -2)
2. 2. Укажіть координати вектора -.
   А (-2; 2) Б (2; -2); В (2; 2)  Г (-2; -2)
3. Укажіть вектор, який дорівнює век­тору .

А  Б  В  Г

II рівень

4. Укажіть координати вектора + .

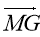А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)

5. Укажіть координати вектора – .

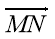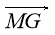А (1; 2)  Б(-1; 2) В (1; -2)  Г(-1; -2)

6. Знайдіть ∙.
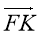   А  Б 2  В 0  Г 1

III рівень

7. При якому значенні п вектори (-1; 1) і 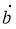(п; -1) коліне­арні?

А n = 1 Б п = -1 В n = ±1  Г ні при яких п

8. При якому значенні п вектори (1; -1) і 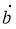(п; 1) перпендику­лярні?

А Ні при яких n   Б n = -1 В n = 1 Г n = ±1

9. Знайдіть координати вершини А паралелограма ABCD, якщо В(1; 0),      C(1; 1), D(-1; 0).

А А(2; 1) Б А(-1; -1) В А(0; 1)  Г А(0; -1)

IV рівень

10. Дано точки A(1; 1), В(2; 1), С(2; 2). Знайдіть внутрішній кут А трикутника ABC.

А 30°  Б 45°  В 60°  Г 90°

11. Знайдіть площу чотирикутника ABCD, якщо A(1; 1), В(2; 3), С(3; 1),     D(2; -1).

А 2  Б 4  В 6  Г 8

12. Знайдіть кут В трикутника ABC, якщо А(0; -1), В(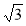; 0), С(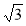; -1).

А 30°  Б 45°  В 60°  Г 90°

Відповіді до тестових завдань

 

Рівень	Номер завдання	Варіант 1	Варіант 2
І	1	В	В
	2	А	А
	3	Б	Г
II	4	В	В
	5	Б	Б
	6	В	В
III	7	Б	А
	8	Б	В
	9	А	Б
IV	10	Г	Б
	11	Б	Б
	12	А	В

 

II. Домашнє завдання

VІІ. Презентація проектів

Учні, які мали завдання перед початком вивчення теми створити проекти у програмі Microsoft Power Point, демонструють їх на комп’ютері (3 проекти «Використання векторів», «Історія появи векторів », «Чи потрібні вектори?»).

VІІІ. ПІДСУМОК УРОКУ

1)Рефлексія:

Що вивчалось на уроці ?

Що найкраще вдавалось ?

Що сподобалось під час уроку, що ні?

Що нового ви дізнались?

Як ви оцінюєте свою працю на уроці?

Чи з’ясували для себе, що із вивченого потребує доопрацювати?

2) Піднімають картки емоційного стану.

---  Заключне слово вчителя:

Про вектори  знання дістали

На запитання відповідали

До знань вершин

Дорогу прокладали

ви з векторами добре знайтесь

бо знадобиться вам вжитті

здебільшого у фізиці

із векторами маємо справи

це сила тяжіння, тертя і тяги,

пружності сили, вектори швидкості та переміщення

в перекладі з латинської

той що несе,

хоча це ще не все,

а отже як підсумок скажемо так:

вчіть геометрію із розумінням

щоб знадобилися вам ті знання

щоб вами гордилися всі покоління

бажаю вам успіху й до побачення!

 

ІХ. ДОМАШНЄ ЗАВДАННЯ

--- ( творче )  самостійно скласти картки для гри в «математичне доміно» з теми «Вектори»

--- ПІДГОТУВАТИСЯ ДО КОНТРОЛЬНОЇ РОБОТИ