Презентація уроку " Теорема Фалеса"

Урок з геометрії в 8 класі. Теорема Фалеса. Підготувала урок : Андрюк Н. М. вчитель математики Банилівського ЗЗСО І-ІІІ ступенів ім. Івана Діяконюка.

Мета уроку. Навчити: свідомому розумінню змісту теореми Фалеса та способу її доведення використовуючи означення та властивості середньої лінії трикутника; формувати вміння використовувати теорему під час розв’язування прикладних задач; узагальнювати отримані раніше знання, інтерпретувати та оцінювати результати, прогнозувати в контексті навчальних та практичних задач, використовувати математичні методи у життєвих ситуаціях. Розвивати: вміння бачити закономірності, аналізувати й узагальнювати інформацію; культуру математичного мовлення та письма учнів, вміння правильно вживати математичну термінологію, грамотно висловлювати власні думки, виконувати логічні переходи в кроках мислення, пізнавальний інтерес, застосування знань з математики в життєвих ситуаціях. Виховувати: старанність, впевненість у власних силах, відповідальність за результати своєї роботи ,командний результат та комунікабельність, патріотизм до Батьківщини.

І. Організація уроку Добрий день, любі учні! Наші завдання сьогодні: Не просто слухати, а й чути!Не просто дивитися, а й бачити!Не просто відповідати, а й міркувати!І головне – дружньо й плідно співпрацювати!

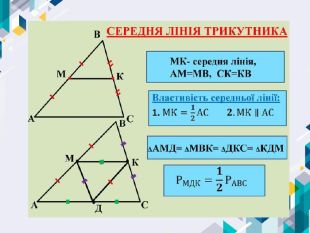
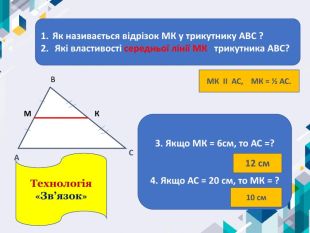
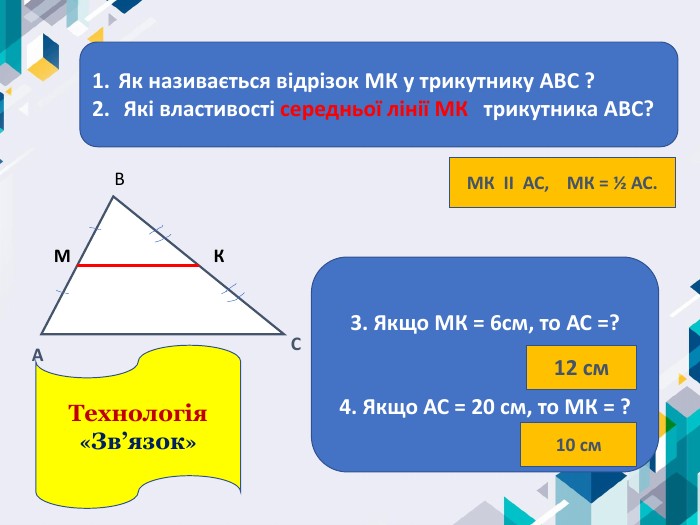
ІІ. Актуалізація знань Прямі, що не перетинаються називаються …Кут – це геометрична фігура, яка складається з двох променів, що мають спільний … Відрізок, що сполучає середини двох сторін трикутника називається…Через точку, що не лежить на даній прямій можна провести … пряму, паралельну даній. Технологія «Незакінчене речення»паралельнимипочаток. Середня лінія трикутника. Одну,єдину

Як називається відрізок МК у трикутнику АВС ? Які властивості середньої лінії МК трикутника АВС?АВСМКМК ІІ АС, МК = ½ АС.3. Якщо МК = 6см, то АС =?4. Якщо АС = 20 см, то МК = ?12 см10 см. Технологія «Зв’язок»

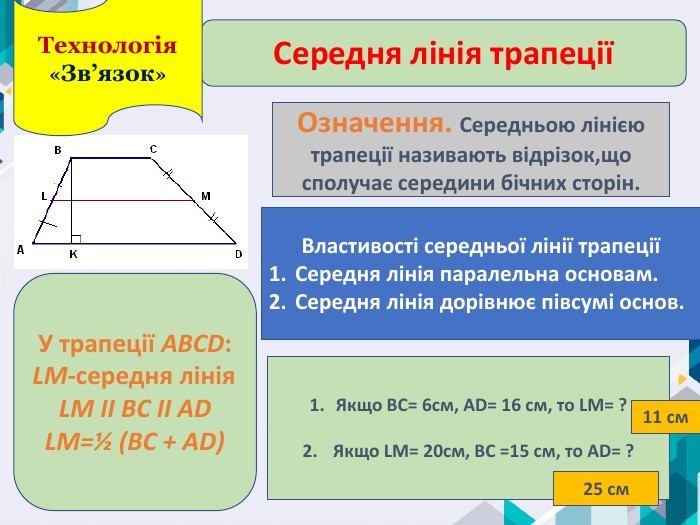
Середня лінія трапеціїОзначення. Середньою лінією трапеції називають відрізок,що сполучає середини бічних сторін. Властивості середньої лінії трапеціїСередня лінія паралельна основам. Середня лінія дорівнює півсумі основ. У трапеції АВСD: LM-середня лінія. LM ІІ ВС ІІ ADLM=½ (BC + AD)Якщо ВС= 6см, AD= 16 см, то LM= ? Якщо LM= 20см, ВС =15 см, то AD= ? 11 см25 см. Технологія «Зв’язок»

Історія Одного вченого ІІІ. Мотивація навчальної діяльності

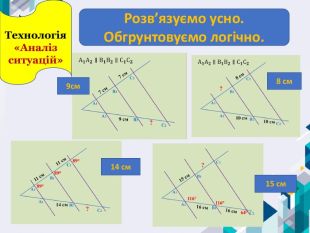
Завдання. Щоб розрізати дошку на 5 рівних частин (рейок), столяр, не вимірюючи її ширини і не виконуючи жодних обчислень, виконує розмітки, показані на малюнку, після чого проводить прямі ВВ1, СС1, ДД1, ЕЕ1. Чи дійсно отримані рейки будуть мати однакову ширину? Що знає столяр, чого не знаєте ви? Відповіддю на поставлені запитання у задачі послужить теорема Фалеса. Це теорема не звичайна, а авторська, названа в честь її творця

Фалес Мілетський (VI ст. до н.е.) був першим із «семи наймудріших» Греції, він був не тільки вченим, а ще й державним діячем, філософом, астрономом. Багато подорожував , особливо по Єгипту. Вивчав досвід єгипетських математиків. Він самостійно визначив висоту єгипетських пірамід , чим здивував єгипетського фараона Амазіса. Повернувшись на батьківщину , заснував Іонійську школу.

Історики вважають , що саме він ввів у геометрію ідею доведення. А також доведення таких теорем: теореми про рівність вертикальних кутів,теореми про рівність кутів при основі рівнобедреного трикутника,другої ознаки рівності трикутників,

Кут, що спирається на діаметр , прямий. А також знайшов розв’язання задачі про визначення відстані до корабля, що перебуває в морі.

В астрономії визначив тривалість року 365 днів, довів, що Земля має форму кулі та передбачив сонячне затемнення 28 травня 585 року до нашої ери. На пам’ятнику йому написано: „Настільки мала ця гробниця, настільки велика слава цього царя в галузі зірок”

ІV. Вивчення нового матеріалу. Формування вмінь. Тема уроку . Теорема Фалеса.„Яка радість особливо велика? Коли вдається досягти бажаного.”Фалес Мілетський. Епіграф уроку

Накреслити кут А. На горизонтальній стороні кута, використовуючи клітинки, відкласти три рівні відрізки. Через кінці відрізків провести паралельні прямі, так, щоб вони перетнули другу сторону кута. За допомогою лінійки виміряти довжини відрізків, що утворилися на другій стороні кута. Порівняти довжини утворених відрізків. Сформулювати у вигляді твердження висновок , який ви отримали під час виконання практичної роботи. Практична робота. А???Відрізки рівні

Узагальнюємо

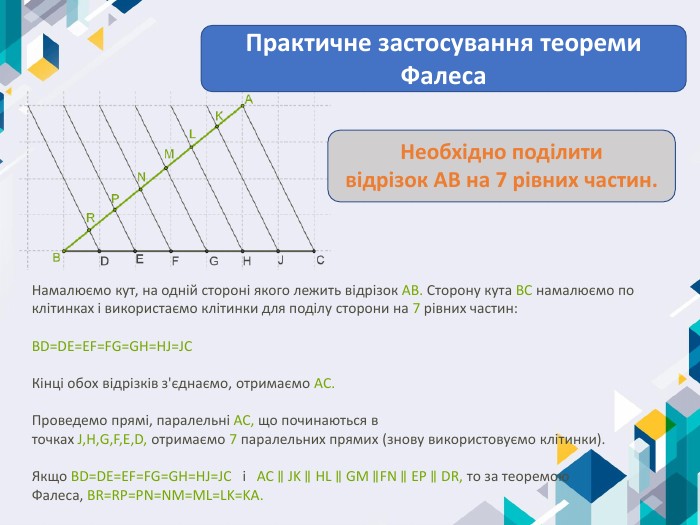
Намалюємо кут, на одній стороні якого лежить відрізок AB. Сторону кута BC намалюємо по клітинках і використаємо клітинки для поділу сторони на 7 рівних частин: BD=DE=EF=FG=GH=HJ=JCКінці обох відрізків з'єднаємо, отримаємо AC. Проведемо прямі, паралельні AC, що починаються в точках J,H,G,F,E,D, отримаємо 7 паралельних прямих (знову використовуємо клітинки). Якщо BD=DE=EF=FG=GH=HJ=JC   і   AC ∥ JK ∥ HL ∥ GM ∥FN ∥ EP ∥ DR, то за теоремою Фалеса, BR=RP=PN=NM=ML=LK=KA. Необхідно поділити відрізок AB на 7 рівних частин. Практичне застосування теореми Фалеса

Завдання. Щоб розрізати дошку на 5 рівних частин (рейок), столяр, не вимірюючи її ширини і не виконуючи жодних обчислень, виконує розмітки, показані на малюнку, після чого проводить прямі ВВ1, СС1, ДД1, ЕЕ1. Чи дійсно отримані рейки будуть мати однакову ширину? Що знає столяр, чого не знаєте ви? Висновок . Отримані рейки будуть мати рівну ширину. Столяр використовує метод поділу відрізка на n рівних частин, основою якого є теорема Фалеса.

V. Закріплення навчального матеріалу

Технологія «Аналіз ситуацій»Розв’язуємо усно. Обгрунтовуємо логічно.9см8 см14 см15 см

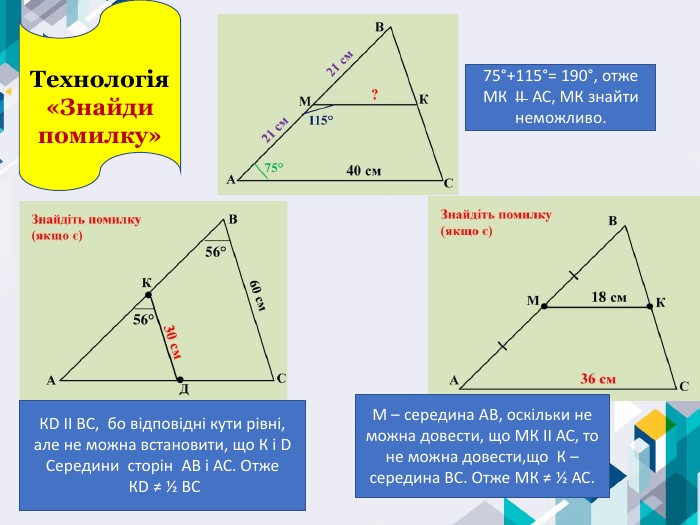
Технологія «Знайди помилку»75°+115°= 190°, отже МК ІІ АС, МК знайти неможливо. КD ІІ ВС, бо відповідні кути рівні, але не можна встановити, що К і D Середини сторін АВ і АС. Отже КD ≠ ½ ВС М – середина АВ, оскільки не можна довести, що МК ІІ АС, то не можна довести,що К – середина ВС. Отже МК ≠ ½ АС.

Працюємо з підручником. Розв’язати задачу № 395. АВСDMKEРозв’язання. У трапеції ABCD ВС ІІAD, МК –середня лінія. МЕ=4см, ЕК =6см. За властивістю середньої лінії МК ІІ ВС ІІ AD, Оскільки АМ = МВ, то за теоремою Фалеса АЕ = ЕС, тобто Е-середина АС. У Δ ВАС МЕ – середня лінія . За її властивістю МЕ = ½ ВС, тоді ВС = 2 МЕ=2·4=8(см). Аналогічно ЕК – середня лінія Δ ACD, тому AD = 2 EK=2·6=12(cм). Відповідь: 8см, 12см.

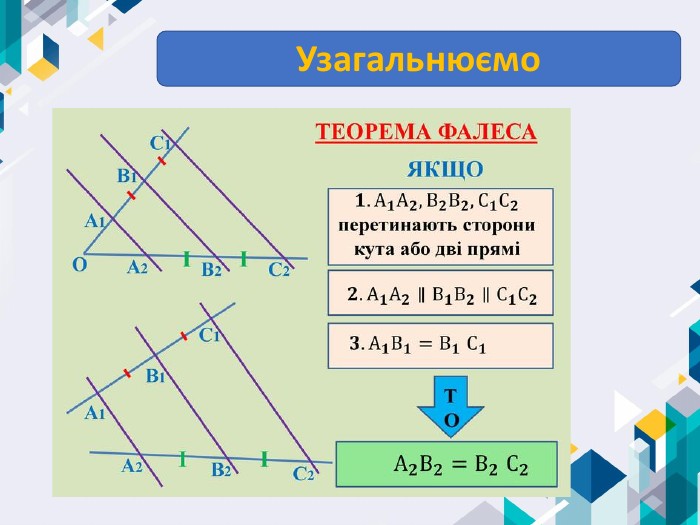
VІ. Підсумок уроку. Алгоритм застосування теореми Фалеса при розв’язуванні задач.1. Встановити , що на одній стороні кута (прямій ) відкладено рівні відрізки.2. Встановити (довести) паралельність прямих, що перетинають дані сторони кута( дані прямі).3. Зробити висновок, що відрізки між паралельними прямими на другій стороні кута (другій прямій) теж рівні.

Епіграф уроку. VII. Рефлексія. Повернемось до епіграфу нашого уроку. Чи вдалося вам досягти бажаного на цьому уроці?Чи відчуваєте ви радість від спілкування на уроці?„Яка радість особливо велика? Коли вдається досягти бажаного.”Фалес Мілетський.

VIII. Домашнє завдання: Вивчити п. 11. ( теорема Фалеса)Виконати № 373, 396, 397 Переглянути фільм за посиланням. Фалес МілетськийІсторія Одного Вченого (знайомство з Великими вченими, які змінили світ)https://www.youtube.com/watch?v=et_Id. DRXLXY