Презентація"Узагальнення з теми Подібність трикутників"
Про матеріал
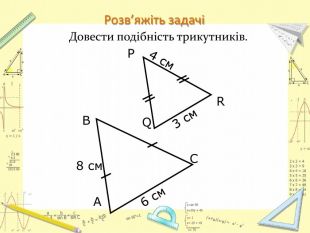
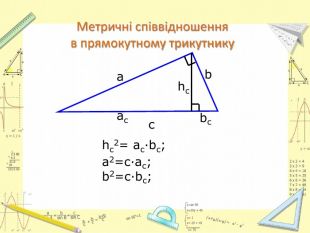
Презентація для урокуГеометрії у 8 класі, узагальнення за темою Подібність трикутників. Підготовка до контрольної роботи. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



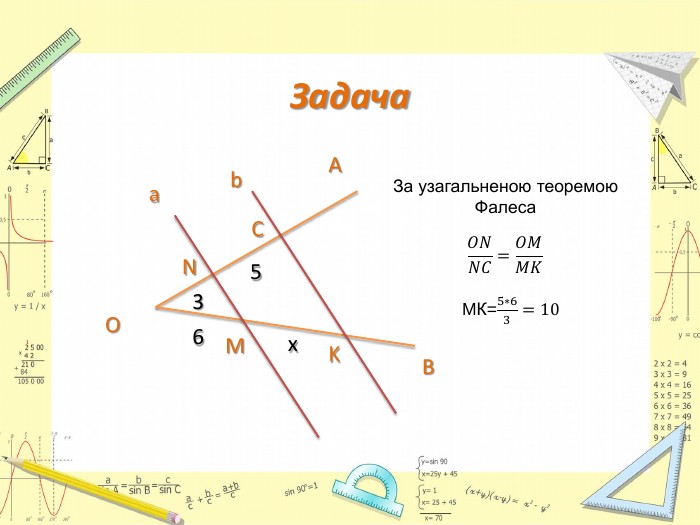
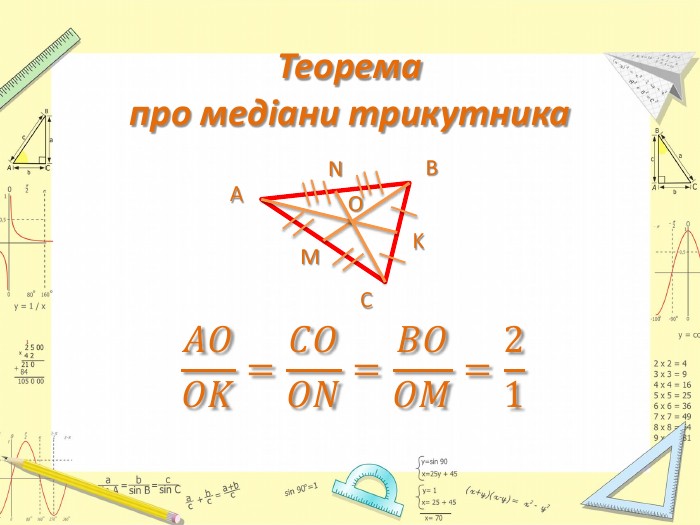



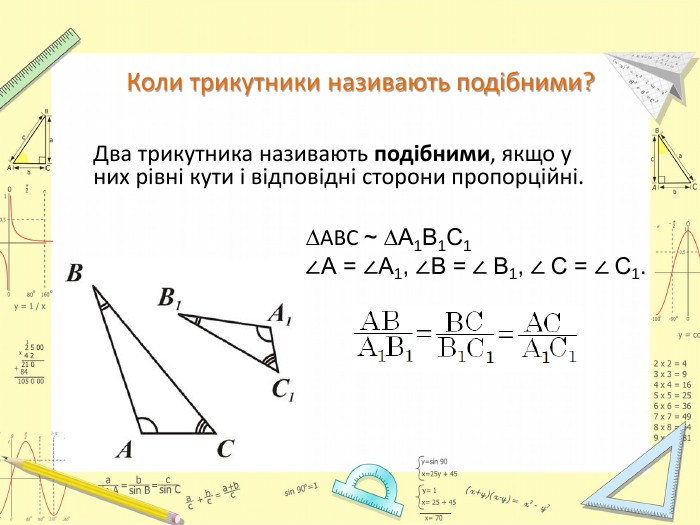


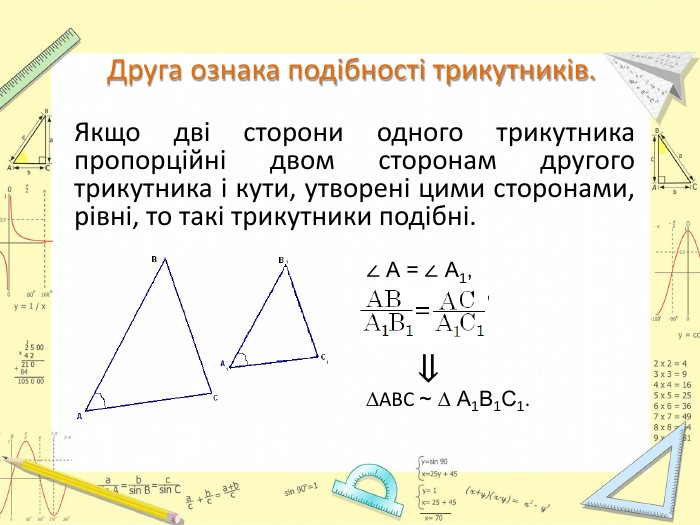


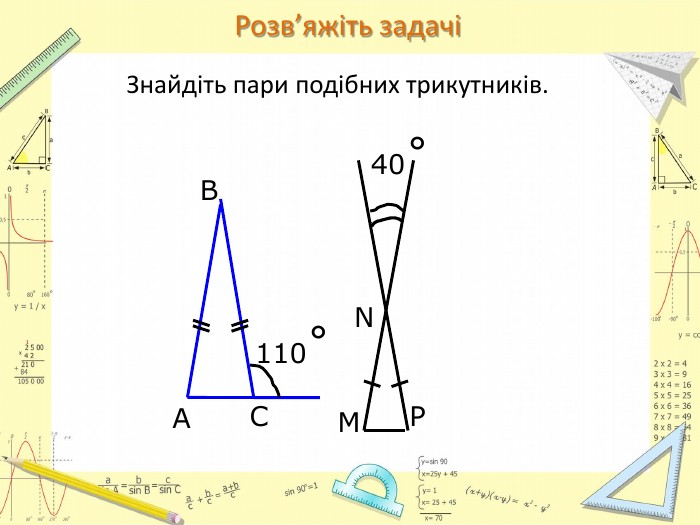

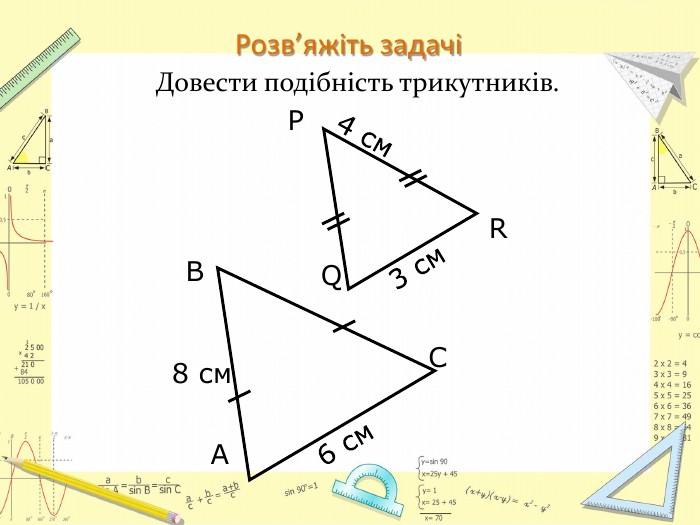

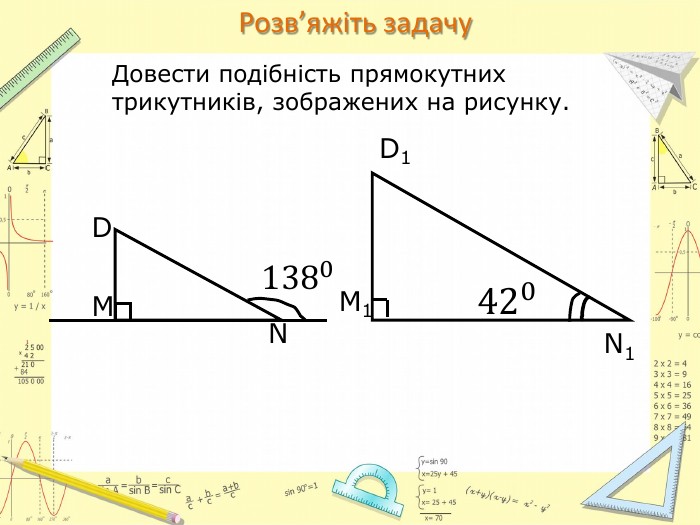
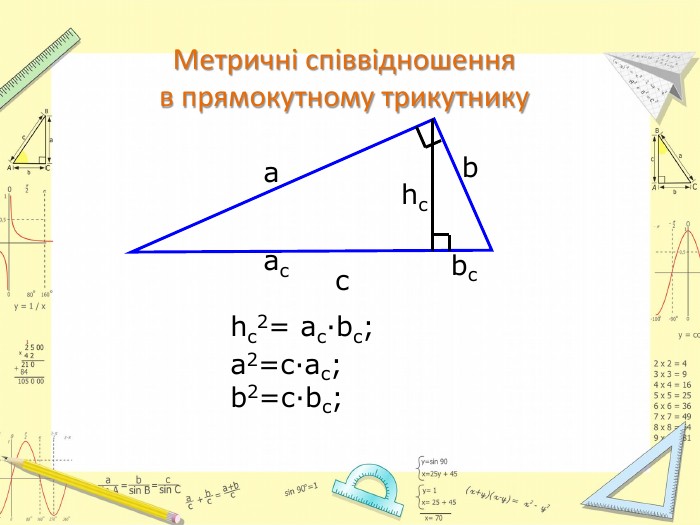


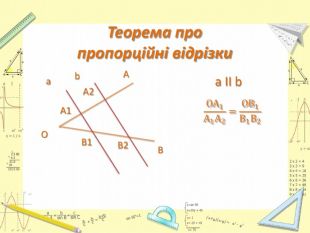




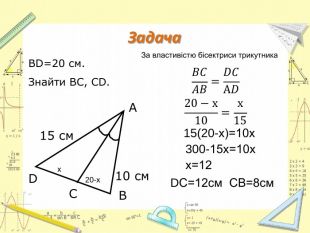




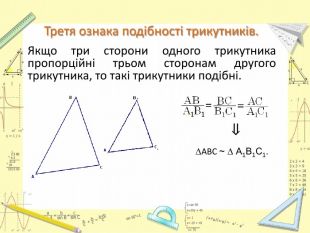

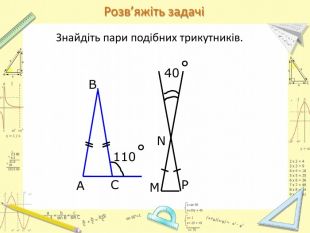




-

Іменинник Людмила Миколаївна
06.05.2024 в 12:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Яковенко Галина Анатоліївна
27.12.2023 в 11:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Поторій Соломія Степанівна
20.11.2023 в 22:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
07.09.2022 в 01:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новіцька Антоніна Володимирівна
29.04.2022 в 11:25
Чудова презентація!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука