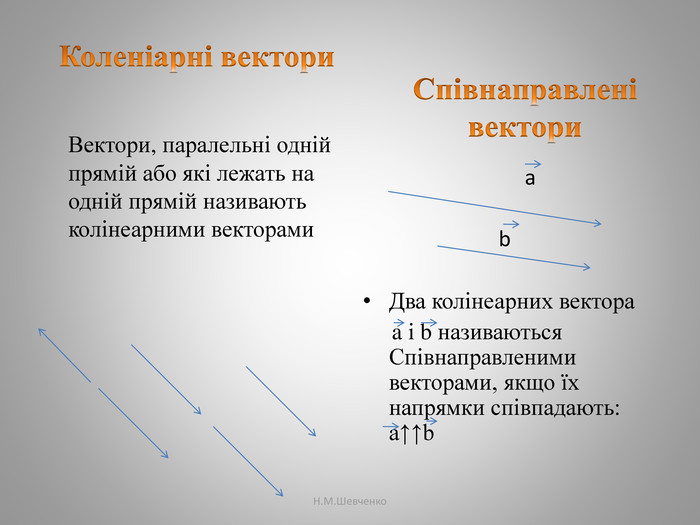
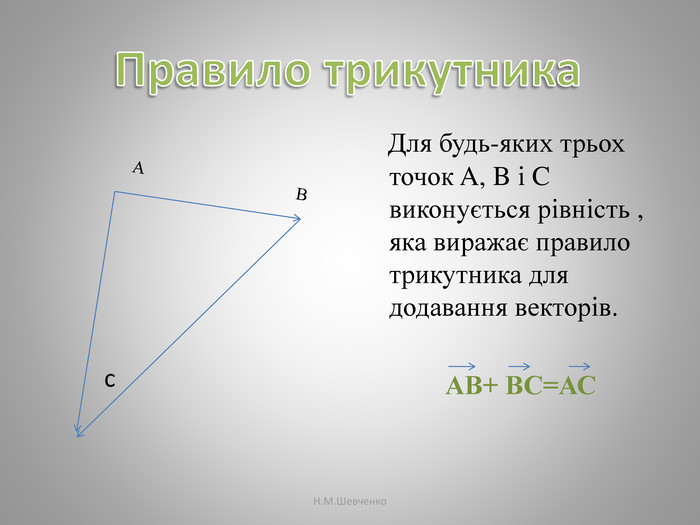
Презентація :Вектори . Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами

Вектори . Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами. Підготувала вчитель математики Шевченко Н. М.

Вектор- це напрямлений відрізок, тобто відрізок, який має довжину і певний напрямок. Графічно вектори зображаються у вигляді напрямлених відрізків прямої певної довжини. АВ ВАН. М. Шевченко

Позначення вектора. Вектор початком якого є точка А, а кінцем - точка В, позначається AB . Також вектори позначають однією маленькою літерою, наприклад a. Довжина вектора. Довжина напрямленого відрізка визначає числове значення вектора і називається довжиною вектора або модулем вектора AB. Для позначення довжини вектора використовують дві вертикальні лінії зліва і справа |AB|. Н. М. Шевченко

Нульовим вектором називається вектор, у якого початкова і кінцева точки співпадають. Нульовий вектор зазвичай позначають як 0. Довжина нульового вектора дорівнює нулю.0. Нульовий вектор Одиничний вектор. Одиничним вектором або ортом - називається вектор, довжина якого дорівнює одиниці. Н. М. Шевченко

Вектори, паралельні одній прямій або які лежать на одній прямій називають колінеарними векторами а b. Два колінеарних вектора a і b називаються Співнаправленими векторами, якщо їх напрямки співпадають: a↑↑b. Коленіарні вектори Співнаправлені вектори. Н. М. Шевченко

Два колінеарних вектора a і b називаються протилежно направленими векторами, якщо їх напрямок протилежний: a↑↓b Вектори a і b називаються рівними, якщо вони лежать на одній прямій або паралельних прямих, їх напрямки співпадають, а довжини рівні . а b. Протилежно направлені вектори аb. Рівні вектори Тобто, два вектори рівні, якщо вони колінеарні, співнаправлені та мають рівні довжини:a = b, якщо a↑↑b і |a| = |b|Н. М. Шевченко

Додавання векторів (сума векторів) a + b - це операція знаходження вектора c, всі елементи, якого дорівнюють попарній сумі відповідних елементів векторів a і b, тобто кожен елемент вектора c дорівнює: сi = ai + bi. Різниця векторів (віднімання векторів) a - b - це операція знаходження вектора c, всі елементи, якого дорівнюють попарній різниці відповідних елементів векторів a и b, тобто кожен елемент вектора c дорівнює: сi = ai - bi. Н. М. Шевченко

с Для будь-яких трьох точок A, B і C виконується рівність , яка виражає правило трикутника для додавання векторів. АВ+ ВС=АСПравило трикутника А ВН. М. Шевченко

Правило паралелограма Н. М. Шевченко

Додавання і віднімання векторів для плоских задач У випадку плоскої задачі суму та різницю векторів a = (ax ; ay) і b = (bx ; by) можна знайти скориставшись наступними формулами:a + b = (ax + bx; ay + by)a - b = (ax - bx; ay – by)Н. М. Шевченко

Формули додавання і віднімання векторів для просторових задач. У випадку просторової задачі суму та різницю векторів a = (ax ; ay ; az) і b = (bx ; by ; bz) можна знайти скориставшись наступними формулами:a + b = (ax + bx; ay + by; az + bz)a - b = (ax - bx; ay - by; az – bz)Н. М. Шевченко

Приклади задач на додавання і віднімання векторів. Приклади плоских задач на на додавання і віднімання векторів. Приклад 1. Знайти суму векторів a = (1; 2) і b = (4; 8). Розв'язок:a + b = (1 + 4; 2 + 8) = (5; 10)Приклад 2. Знайти різницю векторів a = (1; 2) і b = (4; 8). Розв'язок:a - b = (1 - 4; 2 – 8) = (-3; -6)Н. М. Шевченко

Приклади просторових задач на додавання і віднімання векторів. Приклад 3. Знайти суму векторів a = (1; 2; 5) і b = (4; 8; 1). Розв'язок:a + b = (1 + 4; 2 + 8; 5 + 1) = (5; 10; 6)Приклад 4. Знайти різницю векторів a = (1; 2; 5) і b = (4; 8; 1). Розв'язок:a - b = (1 - 4; 2 - 8; 5 – 1) = (-3; -6; 4)Н. М. Шевченко

Вправи на додавання і віднімання двох векторів на площині . Знайдіть значення суми та різниці векторів:1.a = (16; 3) b = (-9; 5)2. a = (-7; -6) b = (0; 7)3.а=(8;-6) b =(8;-12)4. а=(-15;8) b=(-17;-13)Н. М. Шевченко

Вправи на тему додавання і віднімання двох векторів в просторі. Знайдіть значення суми та різниці векторів: 1. a = (14; 13; -20) b = (17; -5; 10)2. a = (-11; -8; 4) b = (3; 16; -17)3. a = (-4; 14; -15) b = (4; 16; -3)Н. М. Шевченко

Вірю не вірю - вектор - це напрямлений відрізок;-вектор - це відрізок що має координати;-вектор – це пряма, що має напрям. Нульовий вектор – це…- вектор, абсолютна величина якого не існує; - вектор, у якого початок співпадає з його кінцем;- вектор, що не має ні початку, ні кінця.колінеарні вектори ?а) якщо вони не лежать на одній прямій; б) якщо вони лежать на одній прямій;в) якщо вони паралельні одній прямій. Сума двох векторів дорівнює одному з векторів-доданків, якщо …а) початок співпадає з його кінцем; б) обидва вектори нульові.в) один із векторів нульовий вектор; Сума двох векторів дорівнює нулю, якщо …а) вектори протилежно напрямлені;б) один із векторів нульовий;в) виходять з однієї точки. Н. М. Шевченко

Дякую за урок !Н. М. Шевченко