Матеріали до уроку геометрії в профільному класі . Тема: Рівняння площини. Рівняння сфери.

               Матеріали до уроків під час карантину.

Тема: Рівняння площини. Рівняння сфери.

                        10 клас. Профільний.

Вчитель: Ласкіна Світлана Миколаївна.

 Криворізька загальноосвітня школа I-III ступенів №45

Мета: Дати учням загальне рівняння площини, рівняння площини,що проходить через точку; поняття вектора нормалі, рівняння сфери. Розглянути умови взаємного розміщення площин.  Розвивати логічне мислення та уміння аналізувати, порівнювати, бачити аналогію задач. Розв’язати типові задачі. Надати учням опорний конспект теми. Пропонувати розв’язати самостійну роботу .

1. Опорний  конспект.

Загальне рівняння площини: Ах+Ву+Сz+Д=0

                                                       А,В,С,Д - числа, одночасно 0

Рівняння площини, що проходить через точку  М(х;у;z):

                      А(х-х)+В(у-у)+С(z-z)=0

Вектор нормалі:     n( А;В;С)  - для площини  Ах+Ву+Сz+Д=0 

 Взаємне розміщення площин:

                    : Ах+Ву+Сz+Д=0

                    : Ах+Ву+Сz+Д=0

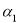1. Площини і 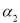- паралельні, якщо

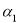2. Площини  і 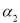- збігаються, якщо

Рівняння сфери: Центр О(а;в;с), радіус R

2. Типові задачі.

1. Для площини  2х-4у+11z-3=0 записати нормальний вектор.

Відповідь: n(2;-4;11)

2. Які з точок: А(2;5;-1), В(3;-6;2) належать площині: 2х-3у+z+12=0

Відповідь: А(2;5;-1)

3. Яке взаємне розміщення площин?

А)5х-3у+3z+2=0    і      10х-6у+6z+12=0

В)5х-3у+3z+2=0    і      10х-6у+6z+4=0

С)5х-3у+3z+2=0    і      10х+6у+6z+12=0

Відповідь: А) паралельні  В) збігаються  С) перетинаються

4. Скласти рівняння площини, що проходить через точку А(2;-5;7) з нормальним вектором  n(2;4;-1)

Розв’язання

                      А(х-х)+В(у-у)+С(z-z)=0

А=2,В=4,С=-1,   значить: 2(х-2)+4(у+5)-1(z-7)=0

   2х+4у-z+23=0

Відповідь: 2х+4у-z+23=0

5. Скласти рівняння сфери з центром у точці О(2;-1;8) і радіусом 5

6. Знайти центр і радіус сфери:

Відповідь: О(2;-1;3), R=3

7. Знайти точки перетину площини  2х-3у+4z+12=0 з осями координат.

Відповідь:  (0;0;-3), (-6;0;0), (0;4;0)

3. Самостійна робота  (Можливо у реальному часі)

https://naurok.com.ua/test/tema-rivnyannya-ploschini-rivnyannya-sferi-10-klas-profilniy-77532.html