Урок "Показникові рівняння"

Про матеріал

Розробку уроку можна використовувати для узагальнення і систематизації знань учні при розв'язуванні показникових рівнянь. до уроку також є презентація

Перегляд файлу

Показникові рівняння

Мета уроку:

узагальнити і систематизувати знання учнів з теми «Показникові рівняння»;
розширювати світогляд учнів;
виховувати бажання працювати в групі, культуру спілкування.

Тип уроку: урок узагальнення і систематизації знань.

Наочність: мультимедійна система: комп’ютер – проектор – екран, конверти для групової роботи із завданнями.

ХІД УРОКУ:

І. Організаційний момент. (слайд 1)

Вчитель вітається з учнями. Діти сідають за парти (парти розташовані так, що утворюється 3 груп і кожному учневі зручно дивитися і на дошку, і на екран.)

ІІ. Перевірка домашнього завдання.

Вчитель перевіряє наявність виконаного домашнього завдання. При виявленні питань з боку учнів вчитель пояснює алгоритм роз’язку. (слайд 2)

6^2х – 36^х– 18 = 0;

6^х = у, тоді

у² – 3у – 18 = 0;

у_{1 +}у₂= 3, у₁ у₂= -18;

у₁ = 6; у₂ = -3.

6^х= 6, х = 1; або 6^х = -3 – розв’язків немає.

Відповідь: 1.

3^х+1 - 23^х-1 – 43^х-2 = 17;

3^х (3 – 2×3^-1 – 4×3^-2) = 17;

3^х (3 – 2/3 – 4/9) = 17;

3^х×17/9 = 17;

3^х = 17 : 17/9;

3^х = 9;

х =2;

Відповідь: 2.

6^х + 6^х-1– 6^х-2 = 7^х– 87^х-2;

6^х ( 1+1/6 + 1/36) = 7^х ( 1 – 8/49);

6^х 41/36 = 7^х × 41/49; | : 7^х , 7^х≠ 0;

6^х: 7^х = 41/49 : 41/36;

(6/7)^х = 36/49;

(6/7)^х =(6/7)²;

х =2;

Відповідь: 2.

3^х = , (розв’язати графічним способом), (слайд 3)

Будуємо в одній системі координат графіки функцій у = 3^х і у = , що перетинаються в точці, абсциса якої дорівнює 0. Отже х = 0.

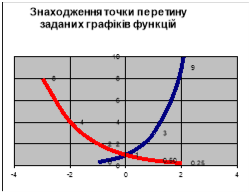у = 3^х

х	0	1	2	3
у	1	3	9	27

у =

х	-2	-1	0	1	2
у	4	2	1	0.5	0.25

Відповідь: 0.

ІІІ. Повідомлення теми та мети уроку та мотивація навчальної діяльності учнів

Вчитель: Сьогодні заключний урок з теми „Показникові рівняння”, метою якого є повторення основних способів розв’язування показникових рівнянь, узагальнення і систематизація здобутих знань про показникові рівняння. (Учні записують в зошиті дату й тему уроку, які заздалегідь записані на дошці)

Вчитель: Ви вже навчилися розв’язувати показникові рівняння, тож вивчаючи той чи інший матеріал обов’язково виникає запитання:- де ж він використовується і навіщо потрібні нам ті чи інші знання. Показникові рівняння застосовуються до розв’язання багатьох задач з фізики, економіки та біології. Одну з таких задач, яка має безпосереднє відношення до нас, я хочу вам запропонувати (слайд 4,5). 26 квітня 1986 року сталася аварія на Чорнобильській атомній електростанції, внаслідок якої територія України була забруднена радіоактивною речовиною.( В цей час на екрані демонструються документальні відеоматеріали про аварію.)

Вчитель: В той день була така сама весна, так само розквітала природа, співали птахи, люди готувалися до вихідних, закохувалися та одружувалися, ростили дітей, раділи життю та готувалися до травневих свят. Та раптом все змінилося в одну мить...

Вчитель: (слайд 6) З фізики відомо математичну формулу закону радіоактивного розпаду. Також відомо, що відношення початкової Ν₀ до кінцевої Ν кількості радіоактивної речовини обчислюється за формулою( на екрані демонструється формула)

де х – час після аварії, Т – період піврозпаду радіоактивної величини.

Задача. Період піврозпаду радіоактивного ізотопу Цезію дорівнює 30 років. За який проміжок часу на забрудненій території після Чорнобильської катастрофи кількість ядер зменшиться в 4 рази, тобто ?

Розв’язок задачі зводиться до розв’язання показникового рівняння.

Діти пропонують спосіб його розв’язання, вчитель записує на дошці.

, , , х = 60.

Відповідь: 60 років.

Вчитель робить висновок: Отже через 60 років кількість ядер радіоактивного ізотопу цезію зменшиться тільки в 4 рази.

ІV. Актуалізація опорних знань.

Розв’язування показникових рівнянь спирається на властивості степеня ( на екран виводяться властивості степеня (слайд 7)). Користуючись ними, усно спростимо вирази, які подано на екрані.

Дошка		Екран
1. СПРОСТИТИ ВИРАЗ		2. ВЛАСТИВОСТІ СТЕПЕНЯ
7¹	7	а¹ = а
11⁰	1	а⁰ = 1, а ≠ 0
9^-х		а^-n = , а ≠ 0
5^х  5³	5³⁺^х	аⁿ × а^m = а^n+m
7⁹  7^х	7^9-х	аⁿ : а^m = а^n-m, а ≠ 0
(6^х)²	6^2х = (6²)^х = 36^х	(аⁿ)^m = а^{m × n}
		, b ≠ 0
6^х5^х	30^х	аⁿ×bⁿ = ( а×b )ⁿ

Тестування за комп’ютерами в програмі My Test. (Програма видає 10 питань із 15 можливих. Виконуючи тестування, учню потрібно вибрати одну правильну із чотирьох запропонованих. На кожне питання відведено 10 секунд).

2^х= 16	3^х = 27	5^х= 25
3^х-1 = 9	5^х-3 = 25	3^х = 1/27
(1/7)^х= 7	2^х= -2	5^-х = 25
27^х= 3	2^х×3^х = 6	10^х = -10
(2/3)^х(3/2)^х =1	(1/25)^х= 5	12^х= 1

V. Узагальнення та систематизація знань.

Форма роботи – групова.( клас ще на початку уроку було поділено на 3 груп.)

Розв’язуючи показникові рівняння ми використовуємо різні способи. Назвіть основні з них.(Діти перелічують основні способи розв’язування показникових рівнянь, після чого вони виводяться на екран (слайд 8)).

Способи розв’язання показникових рівнянь:

Найпростіші рівняння:
- зведення до однієї основи;
- врахування властивостей функції.
Складніші рівняння:
- зведення до однієї основи, введення заміни;
- зведення до однакового показника;
- зведення до двох основ та розв’язування однорідного рівняння;
- винесення спільного множника за дужки та зведення до одного з попередніх способів;
- графічний спосіб;
- використання властивостей функцій;
- використання декількох прийомів.

Кожна група розв’язує рівняння, які отримує на картці та намагається скласти алгоритм розв’язання кожного рівняння.

Завдання на картках: Розв’язати рівняння:

1. = 3⁵^х⁺¹⁰;

9^{– (2}^х^{– 5)}= 3⁵^х^{+ 10};

3^{- 2(2}^х^{– 5)}= 3⁵^х^{+ 10};

3^{- 4х + 10} = 3⁵^х^{+ 10};

-4х + 10 = 5х +10;

-9х = 0;

х= 0.

Відповідь. 0.

2.  = ;

;

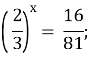
х = 4.

Відповідь. 4.

3. 4^х + 32^х – 4 = 0;

2²^х + 32^х – 4 = 0;

Нехай 2^х = t, тоді

2²^х = t²;

t² + 3t – 4 = 0;

D = 3² - 41 (- 4) = 25;

2^х = 1; 2^х = - 4;

2^х = 2⁰; розв’язків

х = 0. немає.

Відповідь. 0.

Після виконання цього завдання, представник кожної групи біля дошки розповідає алгоритм розв’язування одного із запропонованих рівнянь. Розв’язки при поясненні висвічуються на екран (слайд 9,10). Результатом спільної роботи всіх груп за допомогою вчителя складається загальна схема пошуку розв’язків показникових рівнянь.

VI. Фізкультхвилинка. (слайд 11)

Вчитель: шановні учні, я задаю Вам два питання. Якщо відповідь «так» - присідаємо руки на пояс, якщо «ні» - присідаємо руки вперед.

Небо вночі блакитне? (Ні).
Сонце сяє вдень? (Так).

Наступні два питання. Якщо відповідь «так» - повертаємося вправо, якщо «ні» - вліво.

Сьогодні весна? (Так).
Завтра настане літо? (Ні).

Наступне питання. Якщо відповідь «так» - плескаємо в долоні, якщо «ні» - плескаємо руками по нозі.

Ви сьогодні молодці?

VІІ. Застосування знань учнів до розв’язування показникових рівнянь.

На столі у вчителя є 4 пронумерованих конвертів із рівняннями. Капітан групи підходить до столу і витягує конверт із завданням після чого групи починають розв’язувати запропоновані рівняння. Після того як рівняння будуть розв’язані, учні-представники з кожної групи представляють розв’язання рівняння на дошці, всі інші уважно слухають, виправляють помилки, якщо вони є, записують розв’язання завдань в зошит.

Завдання до групової роботи

Розв’язати рівняння:

1) 4^х⁺¹ + 7×2^х– 2 = 0; 2) 34^х + 29^х = 56^х;