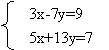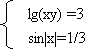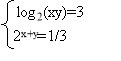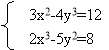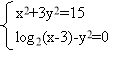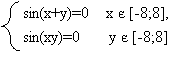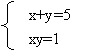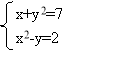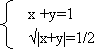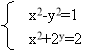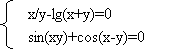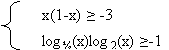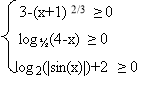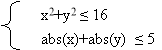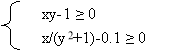Урок з використанням програмного комплексу GRAN1 "Побудова графіків функцій, графічне розв’язування рівнянь та систем рівнянь, нерівностей та систем нерівностей."
Пропоную вам матеріали для проведення уроків з використанням програмного комплексу GRAN1. Ці матеріали допоможуть познайомитися з самою програмою GRAN1 та основними етапами роботи з нею в рамках вивчення тем "Побудова графіків функцій", "Графічне розв'язування рівнянь та систем рівнянь, нерівностей та систем нерівностей."
Використання програми GRAN1 для побудови графіків функцій, графічного розв’язування рівнянь та систем рівнянь, нерівностей та систем нерівностей.
Обладнання. Програма GRAN1 на базі персонального комп’ютера типу IBM PC.
Теоретичні відомості
Програма GRAN1 дозволяє будувати одночасно графіки багатьох функцій. Колір графіка та виразу функціональної залежності співпадають.
Побудова графіків функцій
- Розкриваємо пункт горизонтального меню Об’єкт, вибираємо послугу Створити..
- За допомогою клавіатури або кнопок діалогового вікна вводимо функцію, вказуємо межі проміжку, на якому будемо розглядати функцію та встановлюємо колір для графіка.
- Розкриваємо пункт горизонтального меню Графік, вибираємо послугу Побудувати. На координатній площині з’являється графік функції.
- Для побудови графіків неявно, таблично або параметрично заданих функцій вибираємо у вікні Список об’єктів відповідний пункт та задаємо новий вираз для функції (див. п.1).
- За допомогою послуги Гафік\Масштаб можна змінити масштаб зображення графіка функції.
- Збільшити певну частину графіка функції можна за допомогою миші. Натискуючи ліву кнопку миші обводимо фрагмент графіка, тобто фіксуємо дві протилежні вершини прямокутника, яким обмежується збільшувану частину зображення.
- Якщо у вікні Список об’єктів зняти перемикач біля деяких функцій, та виконати команду Графік\Побудувати- на екрані з’являться графіки тільки відмічених функцій.
- Послуга Графік\Витерти дозволяє стерти зображення графіків функцій.
- Для зняття координат точок графіка використовують послугу Графік\Список точок на графіку\Запис. Внизу екрана з’являється таблиця з координатами відмічених точок (курсор встановлюють у певну точку графіка функції).
- За допомогою послуги Гафік\Мітки можна задати координати та назви точок на графіку.
- Інший спосіб обчислення значення виразу – за допомогою калькулятора. Послуга Операції\Калькулятор.
Графічне розв’язування рівнянь та систем рівнянь.
- Нехай потрібно розв'язати рівняння f(х) = 0, тобто в області визначення функції знайти всі такі значення аргументу х, що відповідні їм значення функції f(x) дорівнюють нулю.
- При графічному поданні функціональної залежності у=f(x) знайти розв'язки рівняння f[x) = 0 означає: знайти всі точки на графіку функції у=f(x), ординати яких дорівнюють нулеві.
- Побудувавши графік функції у=f(x) та скориставшись послугою Графік\Список точок на графіку\Запис, легко визначити ординати всіх точок на графіку функції у=f(x), які в той же час лежать на осі Ох.
- Якщо є потреба уточнити значення коренів, слід збільшити потрібний фрагмент графіку.
- Для розв'язування систем рівнянь одночасно будуємо всі графіки функцій та знаходимо координати точок перетину графіків.
Графічне розв’язування нерівностей та систем нерівностей.
Для графічного розв'язування нерівностей виду f(x)<a або f(x)>a призначено послугу «Нерівність» пункту «Onepaції». При зверненні до послуги «Нерівність» у вікні «Операції» під пунктом «Нерівність» з'являється додаткове вікно з двома пунктами для знаходження відповіді для явно та неявно заданих функцій.
Після того, як вказано потрібний знак нерівності у діалоговому вікні, з'являється відповідь у вікні справа координатної площини, яке називається «Відповіді». А на координатній осі ОХ відмічаються червоним кольором точки, в яких задовольняється вказана нерівність
Розв’язок системи нерівностей виду f1(x)≤0, f2(x) ≤0, ... , fm(x) ≤0 знаходять як множину точок М, в яких задовольняються всі нерівності одночасно, тобто M=M1∩M2∩…∩Mm,. де Мі – множина розв’язків нерівності fi(x)≤0.
Розв’язування системи нерівностей вказаного виду в програмі GRAN1відбувається аналогічно розв’язуванню нерівності.
Графіки функцій типу у=у(х), для яких розглядатиметься система нерівностей, перед зверненням до послуги мають бути побудовані.
Вправи для самостійного виконання:
- Побудувати графіки функцій. Для вказаних значень х визначити значення у. Збільшити масштаб зображення:
1. y= lg(x)+cos(x) x=0; 0.8; 2; 2.5
2. y= 2sin(x)+4 x=0; 1; 1.57; 2;
3. y= cos(2x) x=0; 1; 3; 3.14
4. y= 2x x=0; 1; 2; 3
5. y= ||x-1|-|x-2|| x=-2; -1; 0; 2
6. y= (x-1) 2 *(x-2) 3 x=-3; -1; 0; 4
7. y= (x-1)/(x+2) x=-3; -1; 0; 2
7. y=3√x x=-8; -4; -2; 1
8. y= ½(e x+ e -x ) x=-4; -2; -1; 2
9. y= ½(e x- e -x ) x=-4; -2; -1; 2
10. y=(1+x) x x=0; 1; 2; 5
11. sin(x)/x x=-4; -2; -1; 2
- Подати на екрані одночасно графіки декількох функцій. Стерти зображення графіків. Скрити зображення графіків:
1. y= -2(a2-x2)*(5a2-x2) при a=2; 4; 6
2. y= c(4-x2)*(20-x2) при c=-0.1; -0.5; -2
3. y= -0.5(a2-x2)2 при a=2; 4; 6
4. y= c(16-x2)2 при c=-0.1; -1; -2
5. y= sin(x) y= 2sin(x) y= sin(2x) y= sin(x+2)
6. y= (1.1)x y= (1.2)x y= 2x y= 3x y= 4x
7. y= log2(x) y= log3(x) y= log4(x) y= log(x) y= log1/2(x)
8. y= x2-3 y= 1/(x2-3)
- Побудувати графіки функціональних залежностей, заданих неявно:
1. 0=xy-2
2. 0=1-log2(xy)
3. sin(2(abs(x)+abs(y)))=0
4. sin(sin(xy)+cos(xy))=0
5. sin(2(x2+y2))=0
6. sin(2sqrt(x2+y2))=0
7. 0=sin(32|xy|)/2+x20+y20-1
8. 0=sin(32|xy|)/2+x2+y2-1
9. 0= x20+y20-1+sin(8(xy))
10. 0= x2+y2-1+sin(32xy)
11. sin(x2+y2)4)
12. cos((abs(x)+abs(y))2)
- Знайти наближені розв'язки рівнянь:
|
8. ||х-4|-3| + 4 = 0 |
- При яких а рівняння | x2 -5x + 6 | + a = О матиме найбільшу кількість розв'язків? Найменшу кількість розв'язків? Три розв'язки?
- Використовуючи послуги програми GRAN1, знайти наближені розв'язки систем рівнянь:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VIII. Знайти множини розв'язків нерівностей:
|
1) х2 -7х - 1 ≤ 3; 2) sin(x) ≤ 1/3 при х є [-5, 5]; 3) sin(cos(x)) ≤ cos(sin (x)); 4) 1/log½(x) ≥ -2; 5) х2 - 5х - I ≤ cos(x); 6) |х| +| у| ≤ 5:
|
7) (х – 1)2 + (у -1)2 ≤ 9; 8) sin(sin(xy) + cos(xy)) ≤ 0 при x є [-5, 5], у є [-5, 5] 9) sin(|x|+|y|) ≤ 0 10) xcos(x)+ log½(2-x/5) ≥ 0 11)х4/150- х3/52- х2/3 -1 >-2
|
IX. Знайти множини розв'язків систем нерівностей:
|
|
|
|
|
5. |
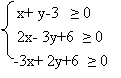 3.
3.
X. Знайти множини розв'язків систем лінійних нерівностей:
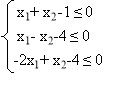 1. 2.
1. 2.
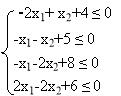
3.
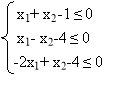


про публікацію авторської розробки
Додати розробку