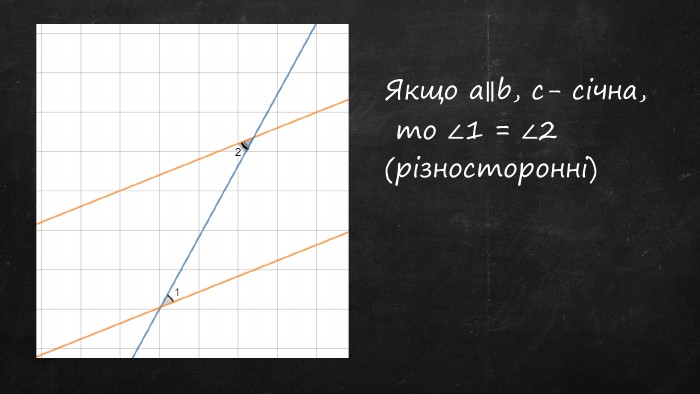
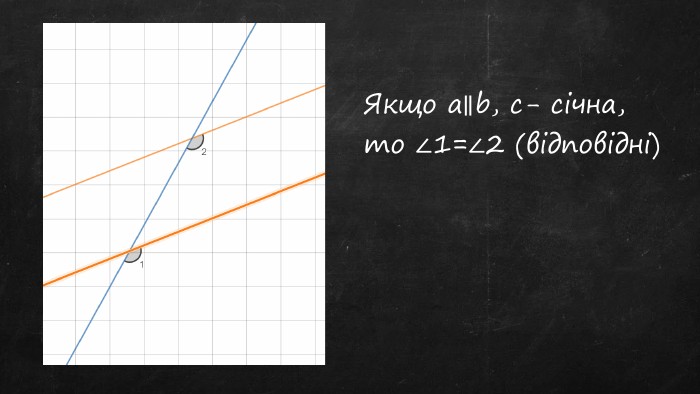
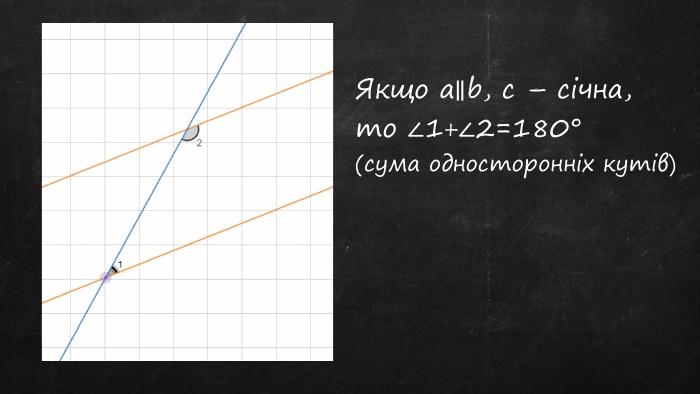
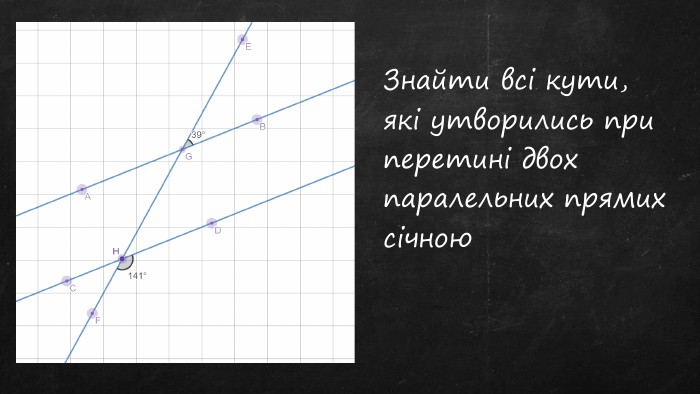
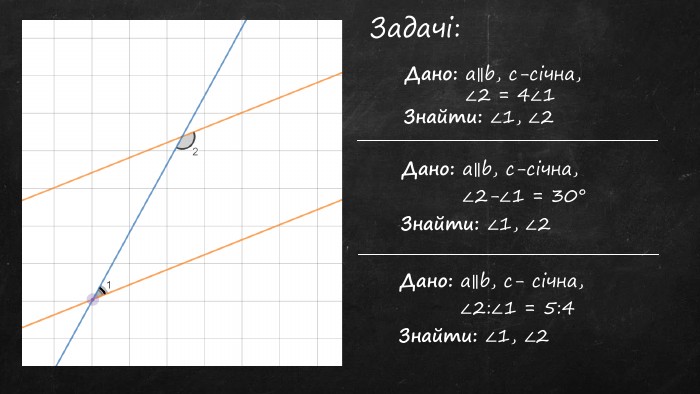
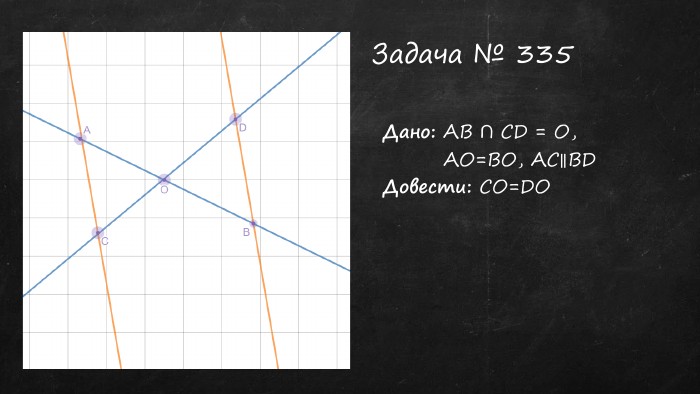
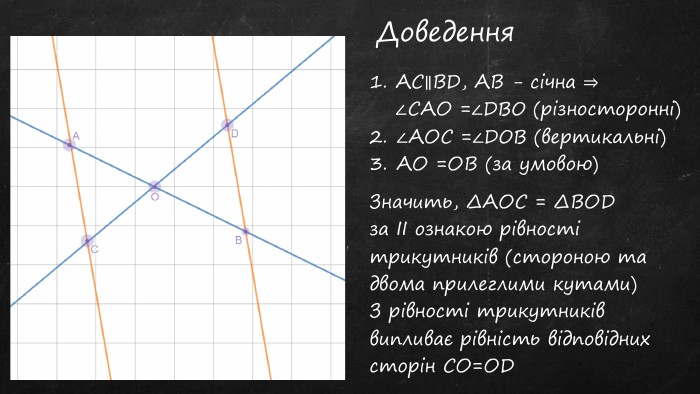
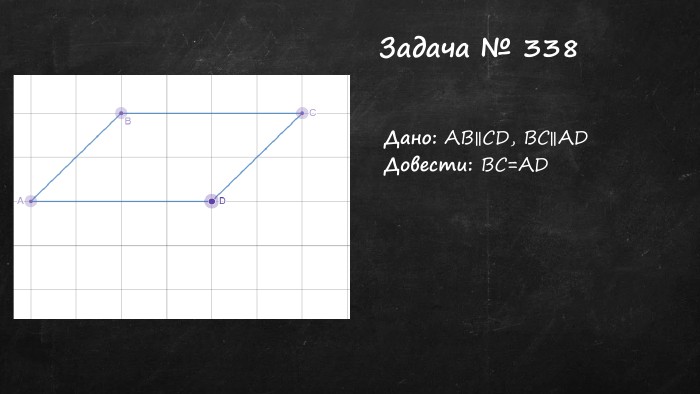
Презентація "Властивості паралельних прямих"
Про матеріал
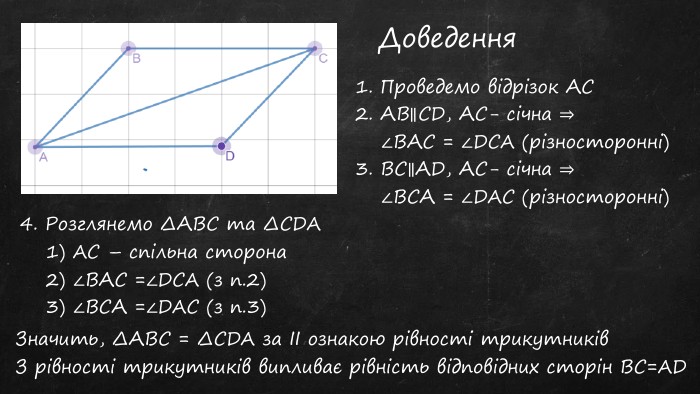
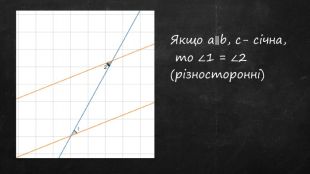
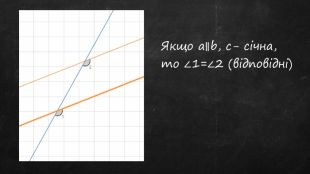
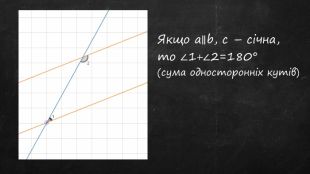
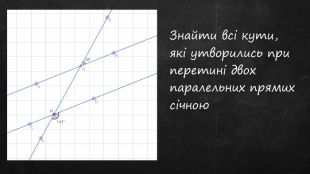
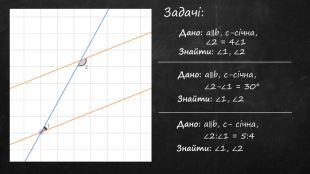
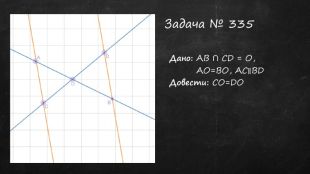
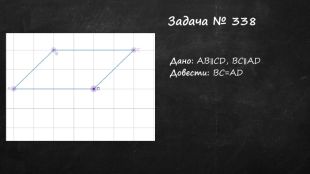
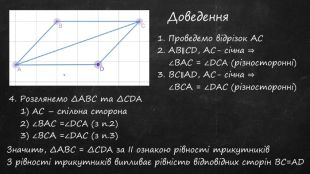
Презентація до уроку, містить теоретичний матеріал, задачі для усного розв'язку та з повним поясненням. Підручник "Геометрія 7 клас" авт. А.Г.Мерзляк Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку