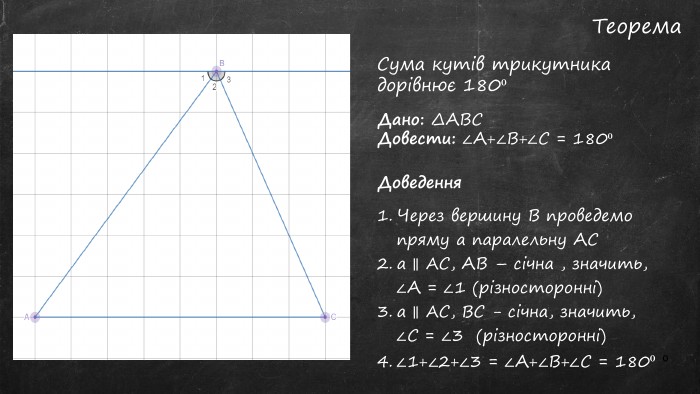
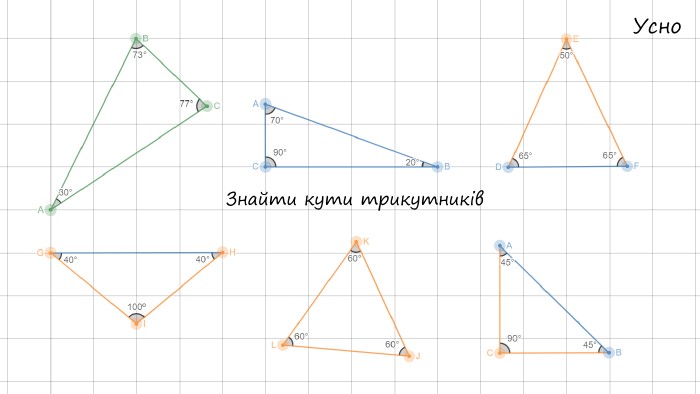
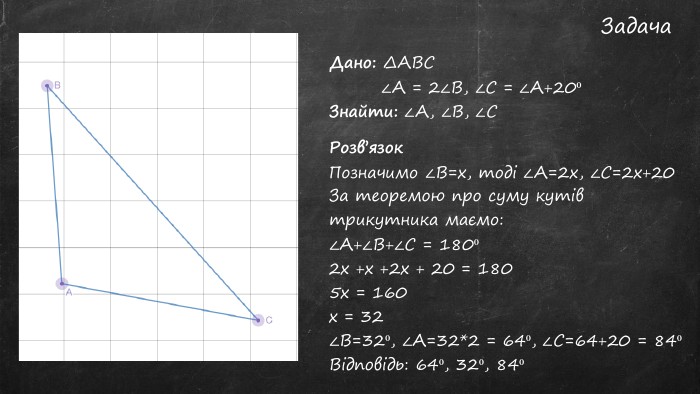
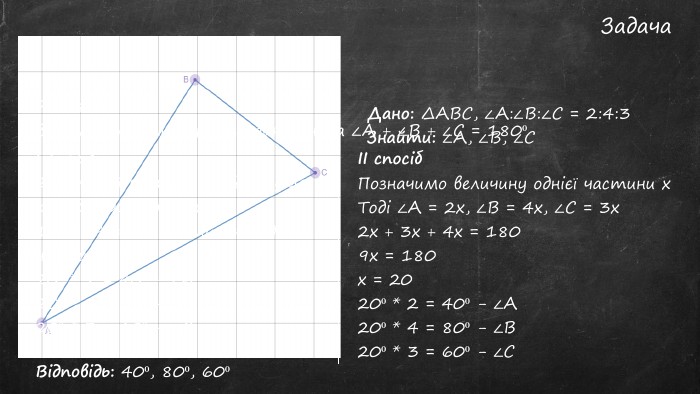
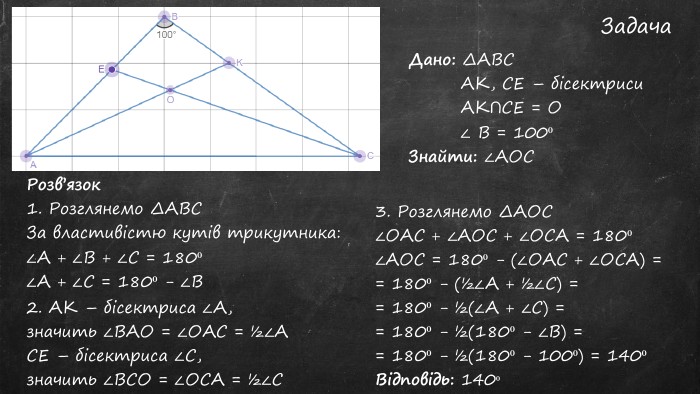
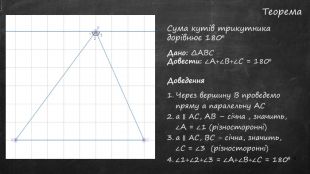
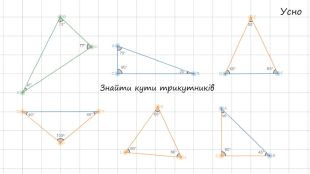
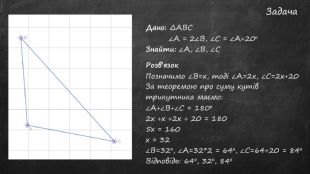
Презентація "Сума кутів трикутника"
Про матеріал
Презентація може бути використана як на уроці так і для самостійного вивчення матеріалу.
Презентацію треба запускати тільки в режимі демонстрації, тригером запуску всіх анімацій є ПКМ Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку