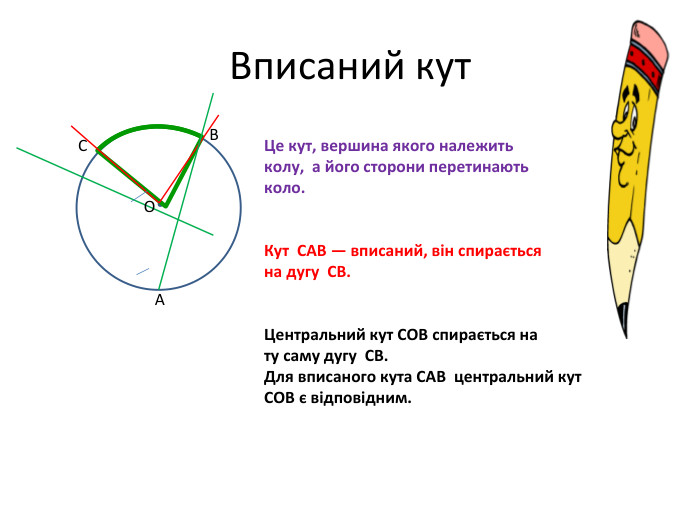
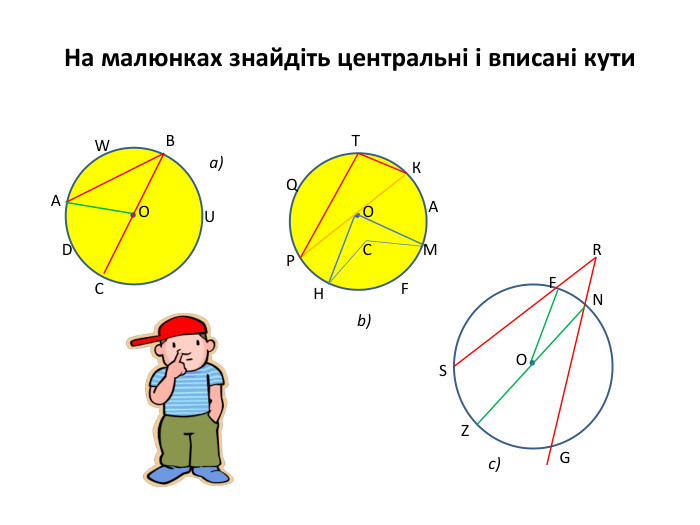
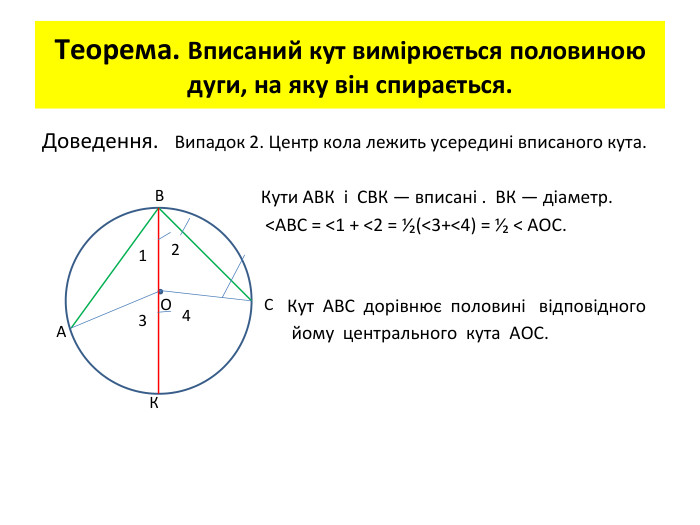
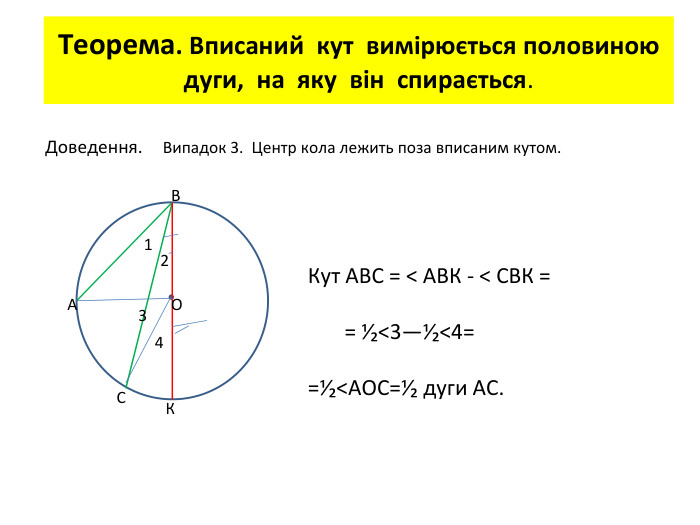
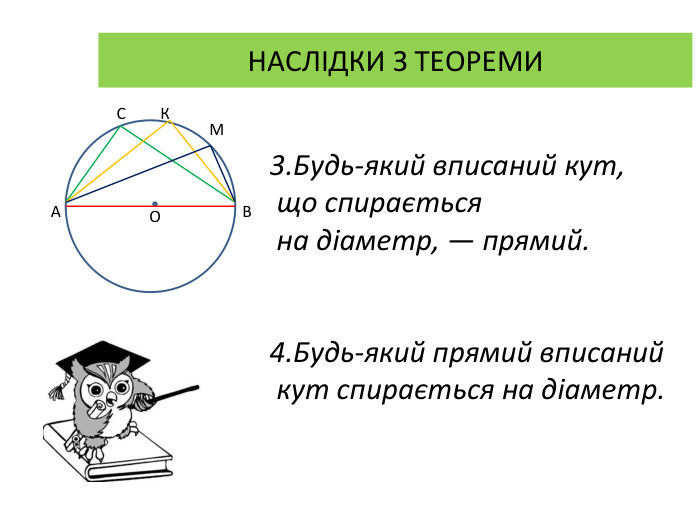
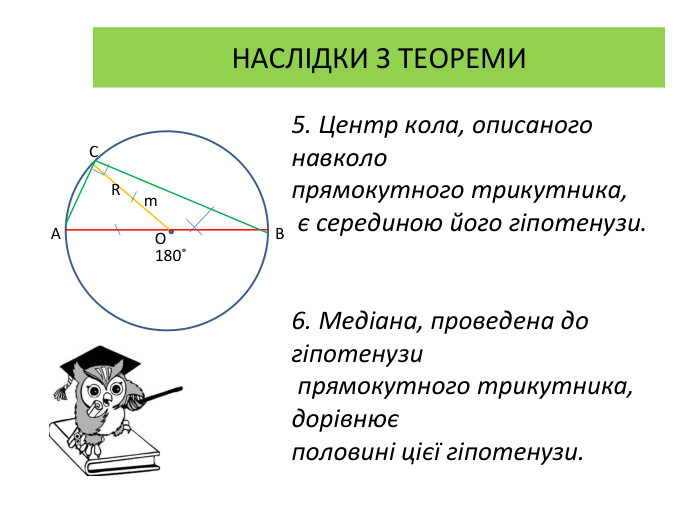
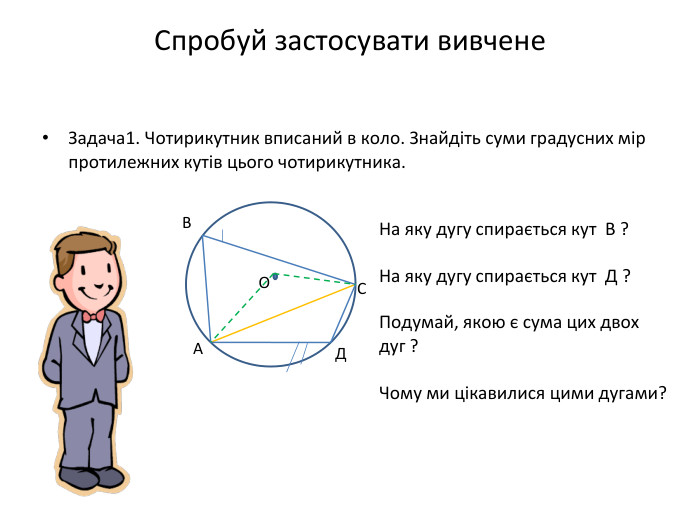
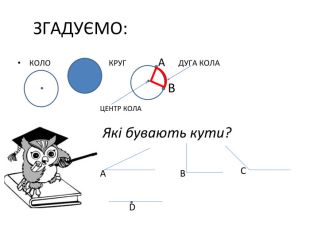
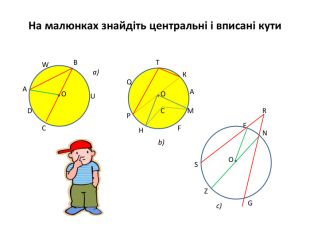
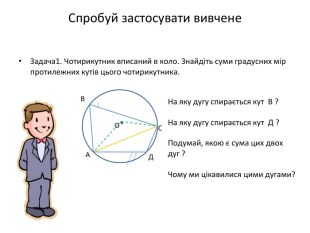
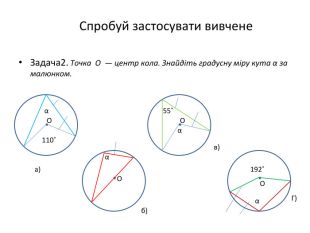
Презентація "Вписані та центральні кути"
Про матеріал
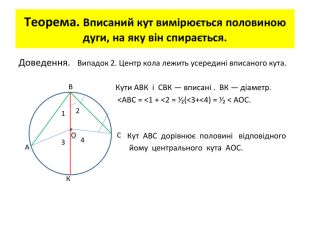
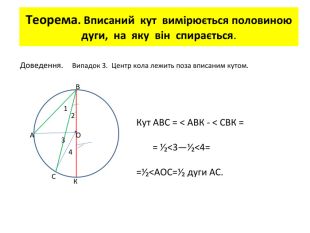
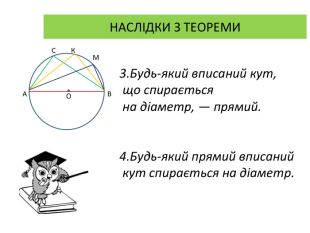
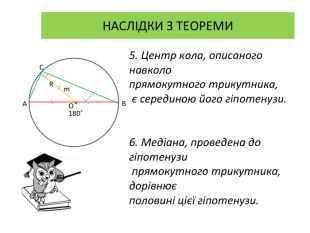
Презентація до уроку вивчення нового матеріалу з теми "Вписані та центральні кути". Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку