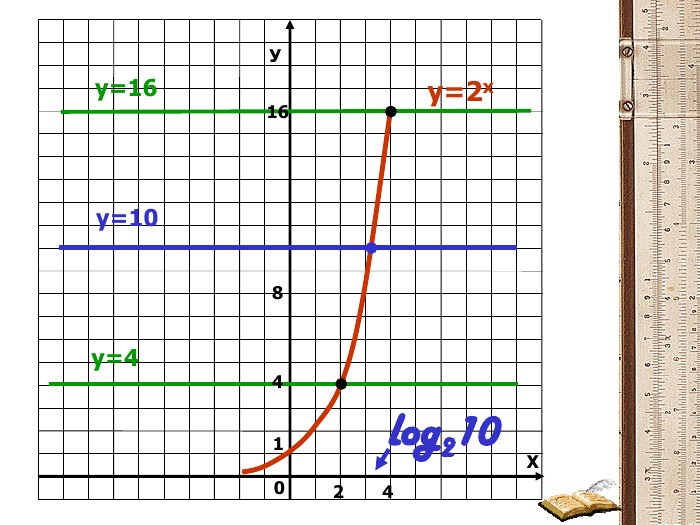
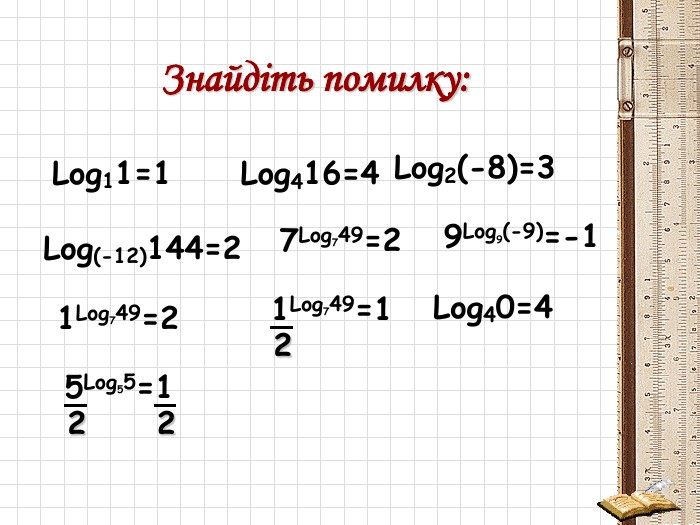Презентація з алгебри та початків аналізу на тему:"Поняття логарифма.Деякі властивості логарифма"
Про матеріал
Даний матеріал буде корисний при введенні поняття логарифма,він містить цікаві вправи та істричний матеріал. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку