Презентація з геометрії для учнів 11 класу на тему "Комбінації геометричних тіл".
Про матеріал
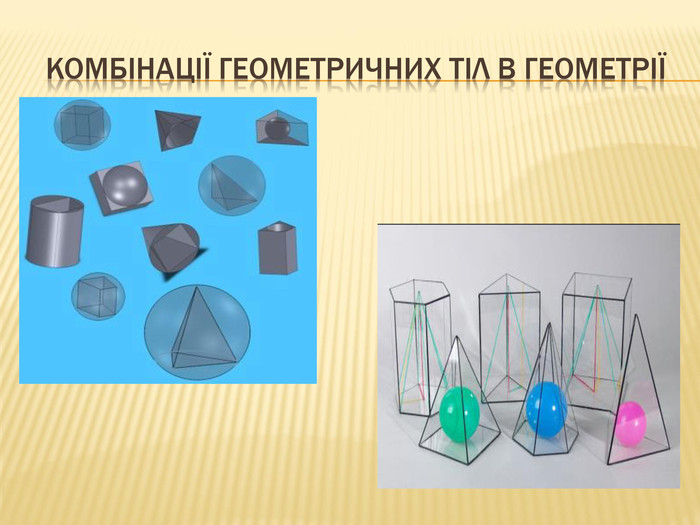
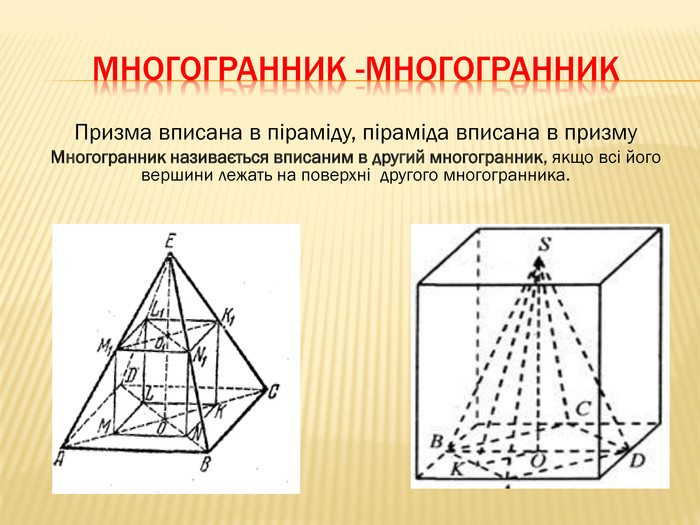
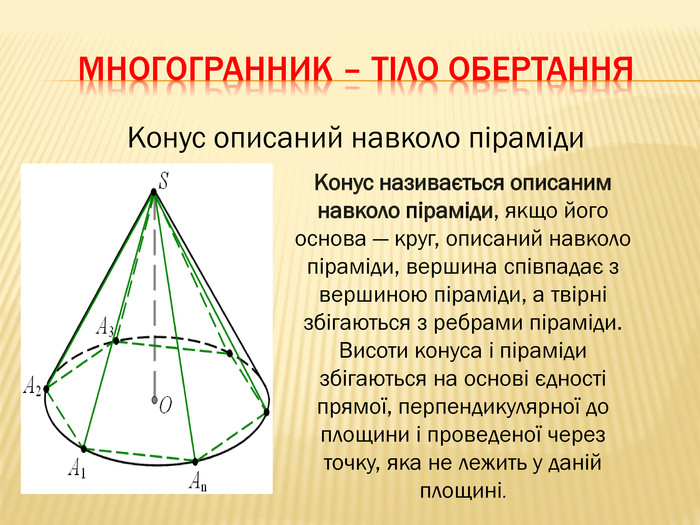
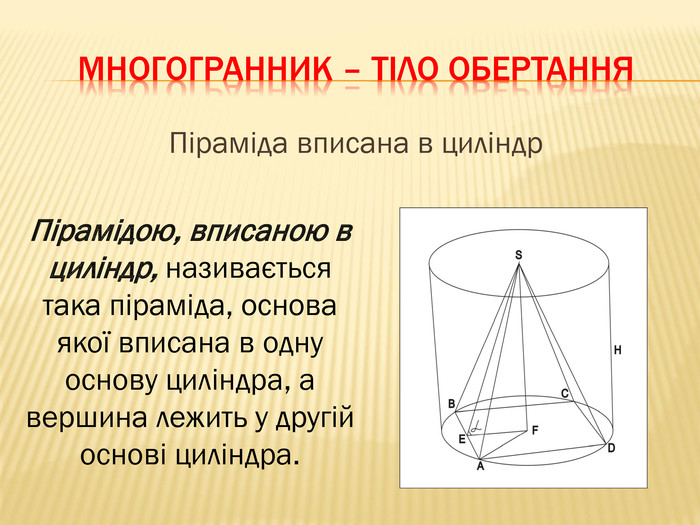
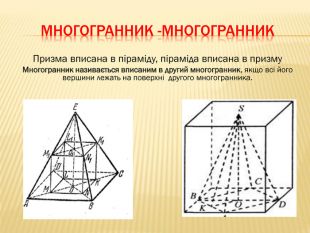
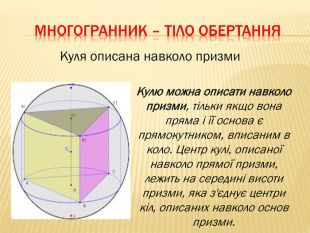
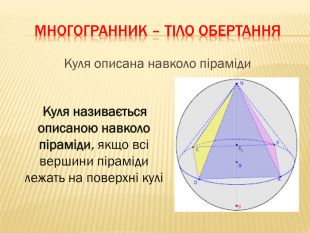
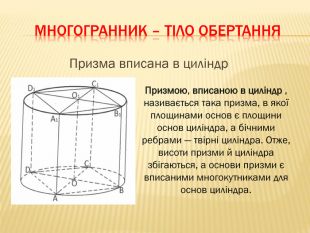
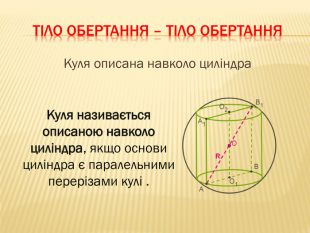
Дана презентація містить відомості про застосування комбінації тіл в архітектурі, навколишньому середовищі, побуті та геометрії. У ній наведено класифікацію комбінацій тіл. В презентації наведено приклади усіх типів можливих комбінацій геометричних тіл з означеннями.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Апостолова Г.В.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку










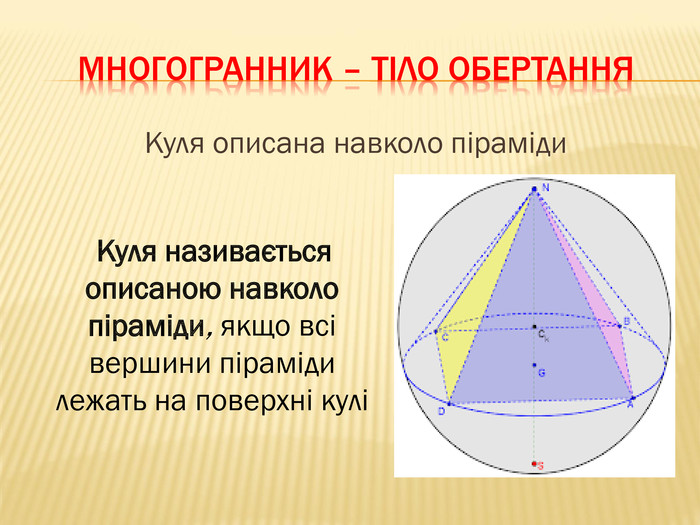

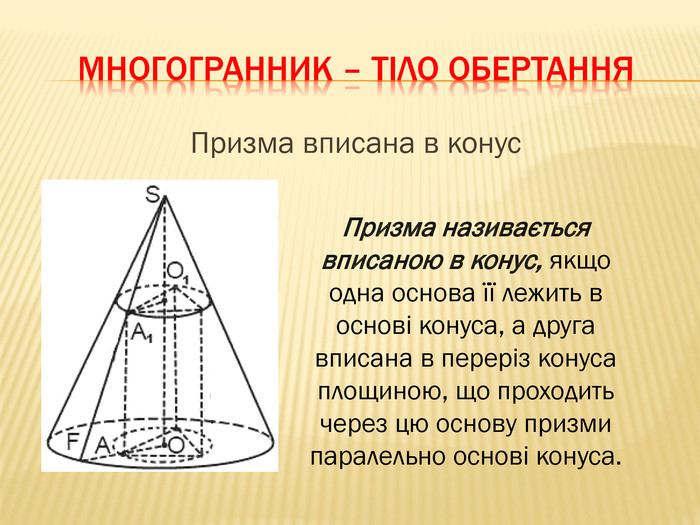
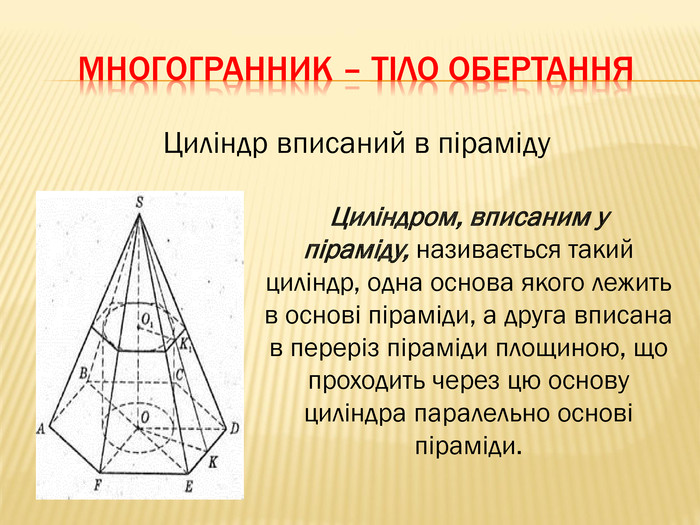
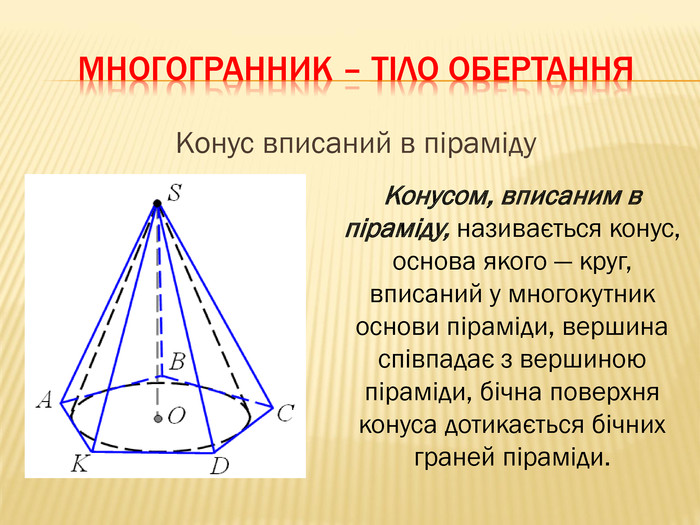
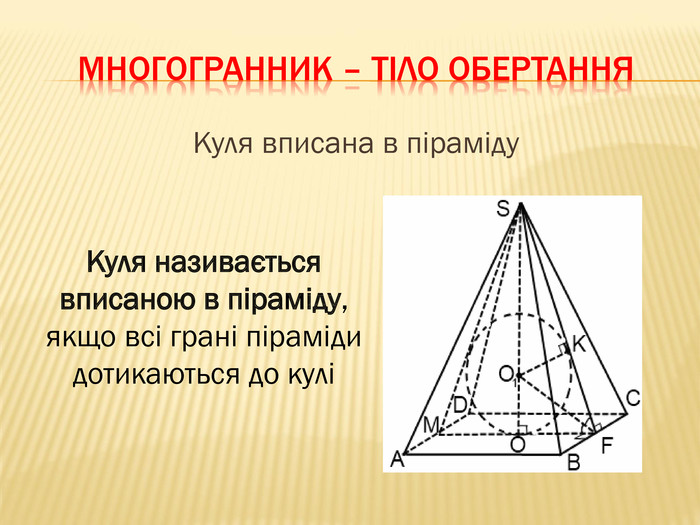
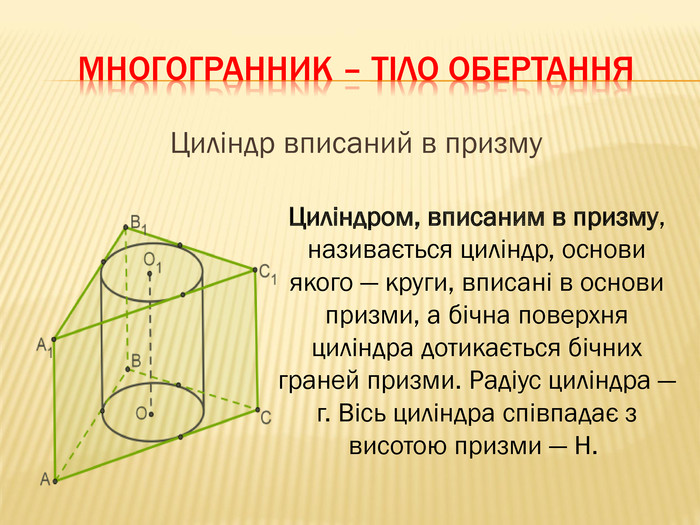


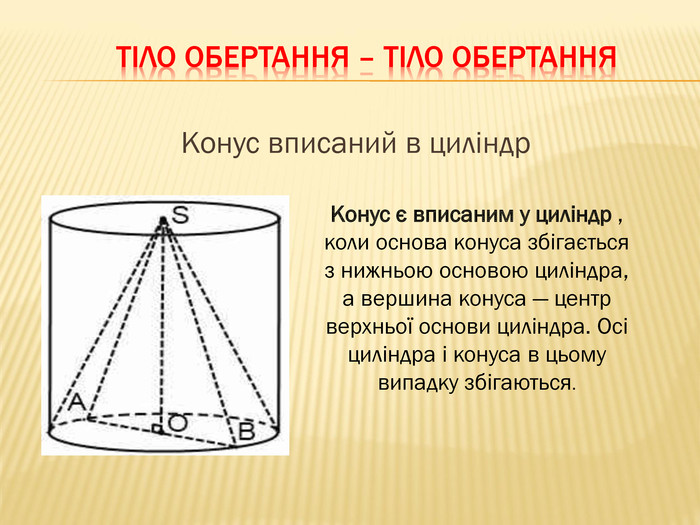
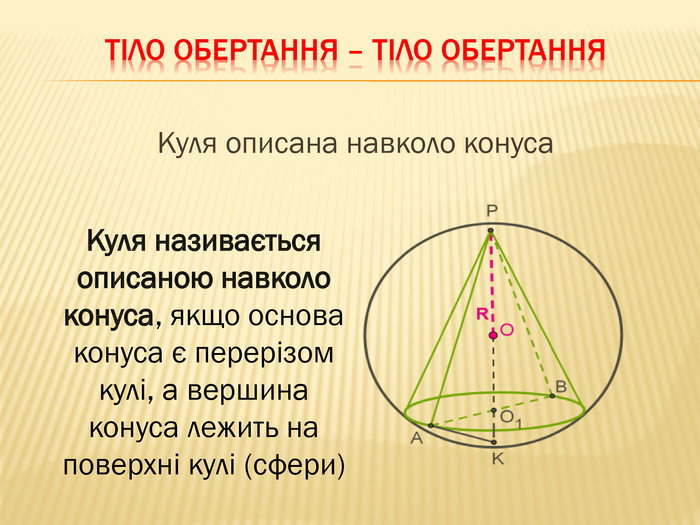















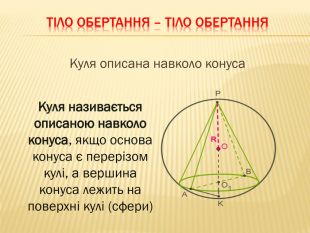
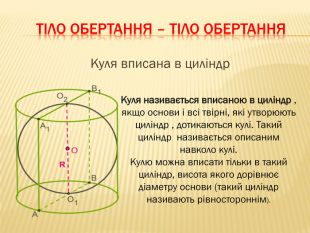
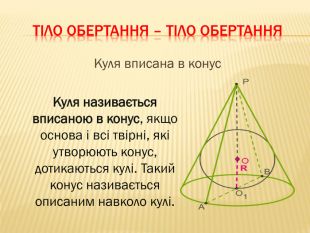
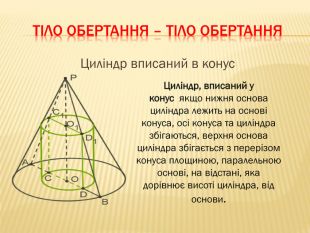
-

Кононенко Ирина Александровна
24.03.2021 в 23:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Некрасова Наталія Володимирівна
23.03.2018 в 19:48
Класно
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Некрасова Наталія Володимирівна
23.03.2018 в 19:21
++++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Костюк Інна Володимирівна
13.03.2018 в 21:17
Дуже гарна презентація. Рекомендую для виконання.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук