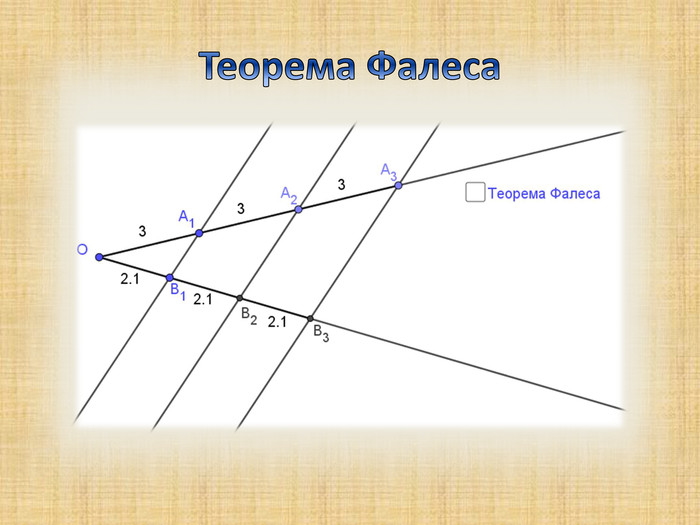
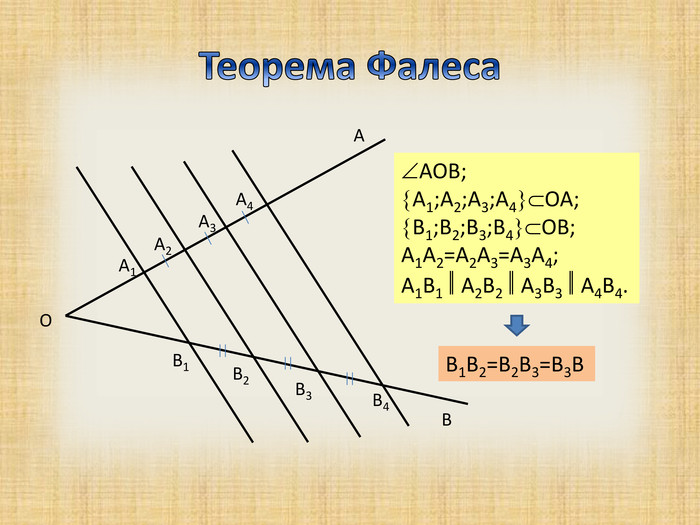
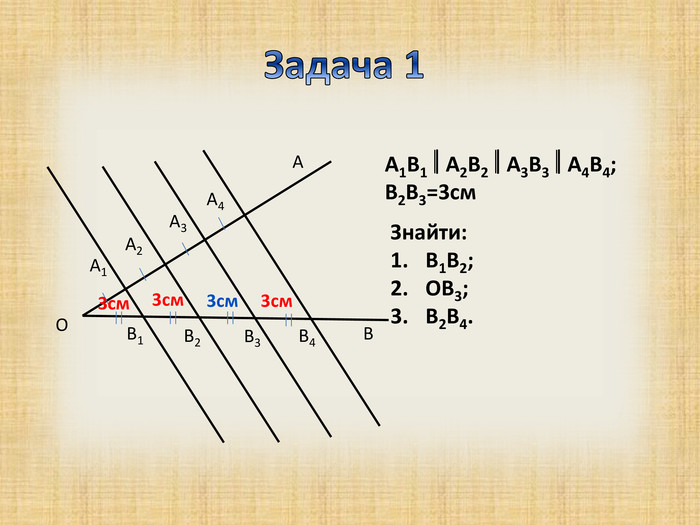
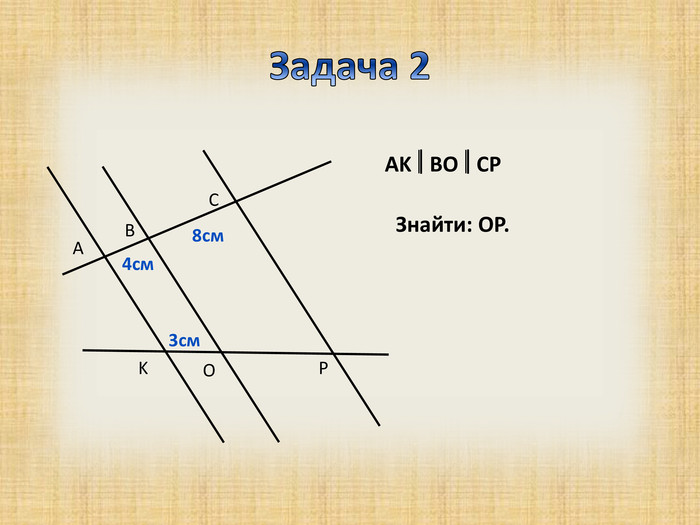
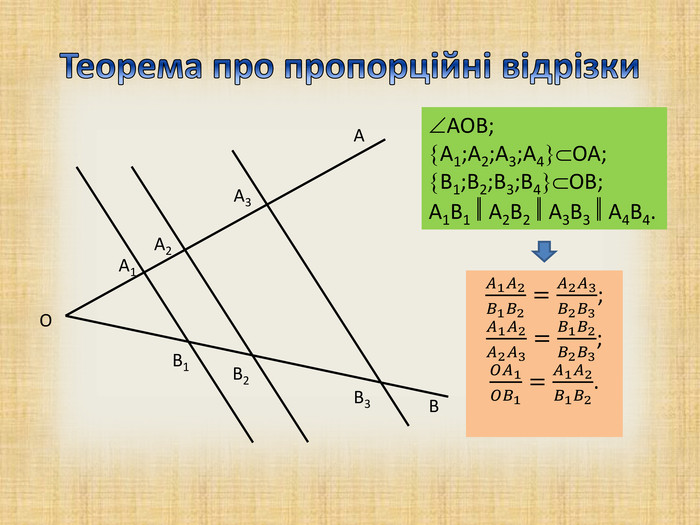
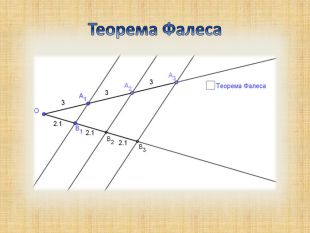
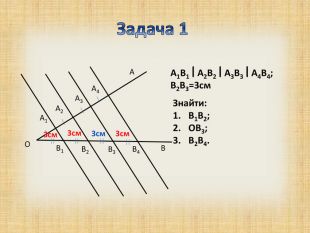
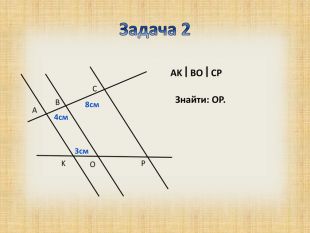
Презентація з теми "Теорема Фалеса для 8 класу"
Про матеріал
Дана презентація підходить для вивчення теми "Теорема Фалеса", при роботі з учними 8 класу Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку