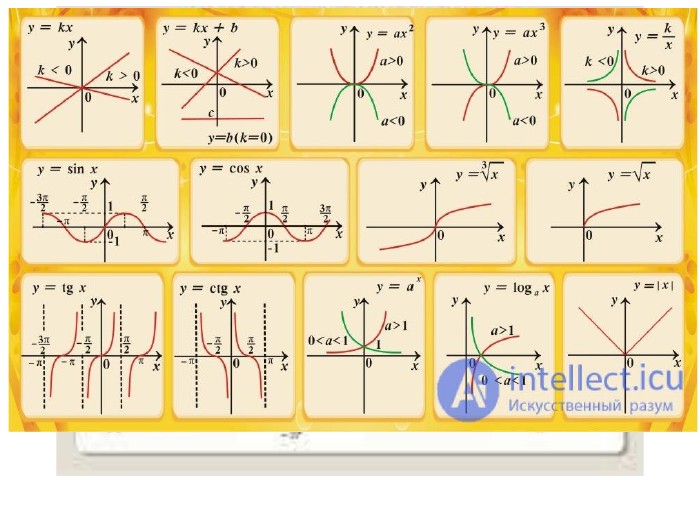
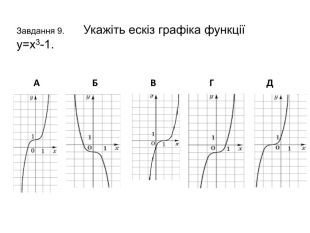
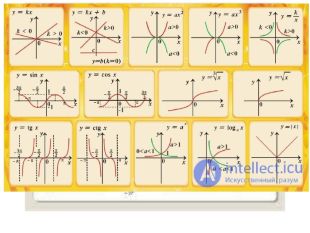
Презентація з теми: " Властивості функцій. Перетворення графіків функцій"
Про матеріал
Тест-контроль з теми: "Властивості функцій. Перетворення графіків функцій." 10 клас. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


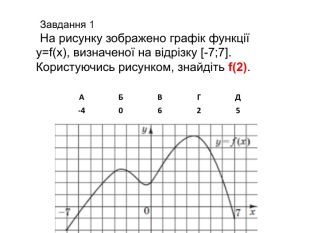
![АБВГД-40625 Завдання 1 На рисунку зображено графік функції y=f(x), визначеної на відрізку [-7;7]. Користуючись рисунком, знайдіть f(2). АБВГД-40625 Завдання 1 На рисунку зображено графік функції y=f(x), визначеної на відрізку [-7;7]. Користуючись рисунком, знайдіть f(2).](/uploads/files/261243/345423/397678_images/2.jpg)
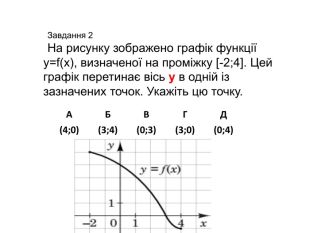
![АБВГД(4;0)(3;4)(0;3)(3;0)(0;4)Завдання 2 На рисунку зображено графік функції y=f(x), визначеної на проміжку [-2;4]. Цей графік перетинає вісь у в одній із зазначених точок. Укажіть цю точку. АБВГД(4;0)(3;4)(0;3)(3;0)(0;4)Завдання 2 На рисунку зображено графік функції y=f(x), визначеної на проміжку [-2;4]. Цей графік перетинає вісь у в одній із зазначених точок. Укажіть цю точку.](/uploads/files/261243/345423/397678_images/3.jpg)
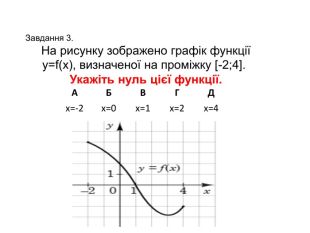
![АБВГДx=-2x=0x=1x=2x=4 Завдання 3. На рисунку зображено графік функції y=f(x), визначеної на проміжку [-2;4]. Укажіть нуль цієї функції. АБВГДx=-2x=0x=1x=2x=4 Завдання 3. На рисунку зображено графік функції y=f(x), визначеної на проміжку [-2;4]. Укажіть нуль цієї функції.](/uploads/files/261243/345423/397678_images/4.jpg)
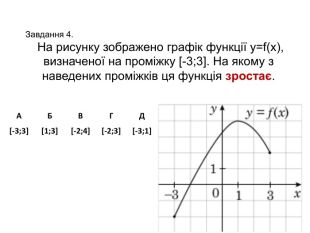
![АБВГД[-3;3][1;3][-2;4][-2;3][-3;1]Завдання 4. На рисунку зображено графік функції y=f(x), визначеної на проміжку [-3;3]. На якому з наведених проміжків ця функція зростає. АБВГД[-3;3][1;3][-2;4][-2;3][-3;1]Завдання 4. На рисунку зображено графік функції y=f(x), визначеної на проміжку [-3;3]. На якому з наведених проміжків ця функція зростає.](/uploads/files/261243/345423/397678_images/5.jpg)
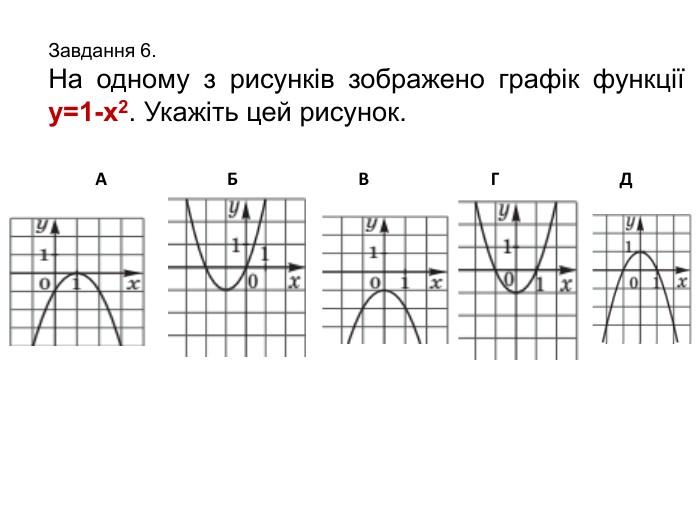
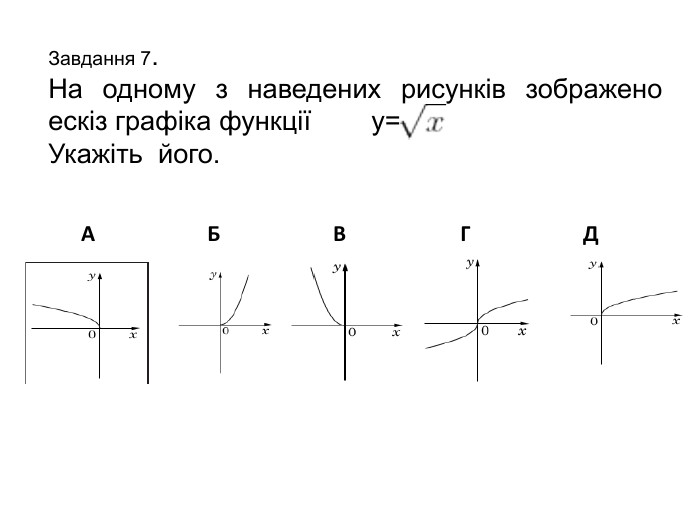
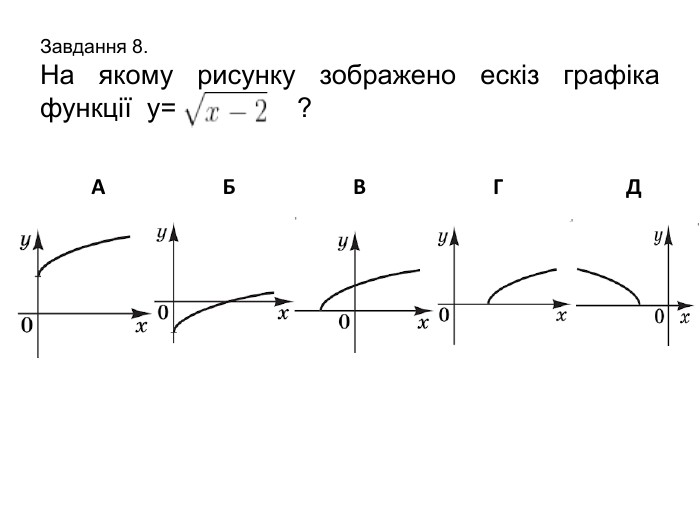
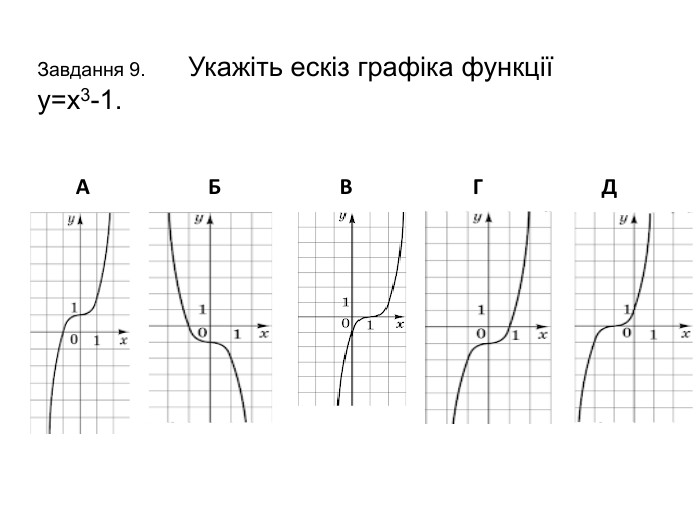
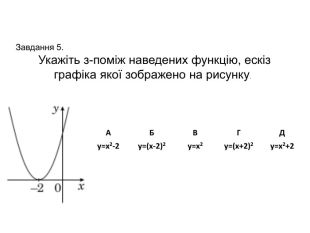
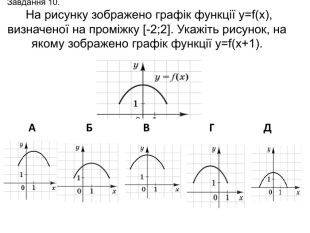
![Завдання 10. На рисунку зображено графік функції у=f(x), визначеної на проміжку [-2;2]. Укажіть рисунок, на якому зображено графік функції y=f(x+1). АБВ Г Д Завдання 10. На рисунку зображено графік функції у=f(x), визначеної на проміжку [-2;2]. Укажіть рисунок, на якому зображено графік функції y=f(x+1). АБВ Г Д](/uploads/files/261243/345423/397678_images/11.jpg)