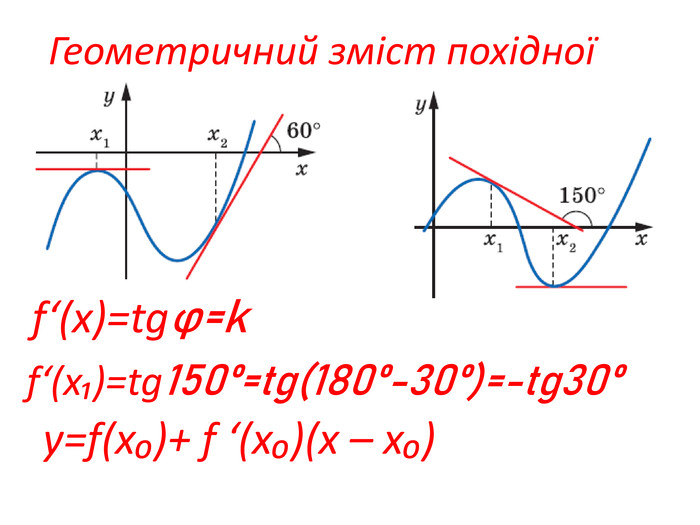
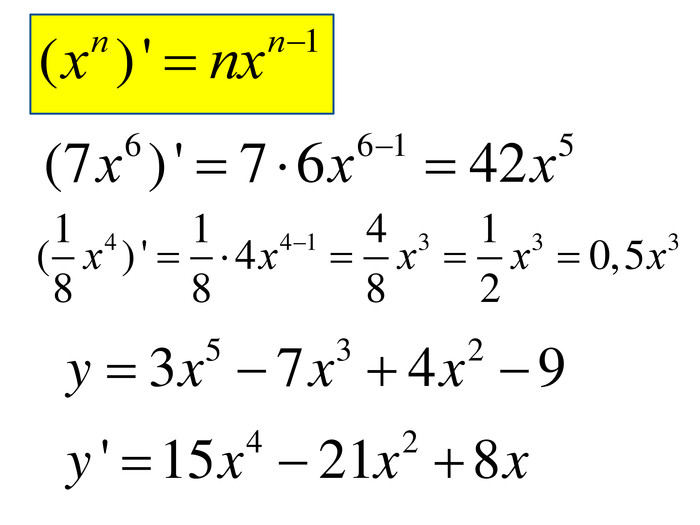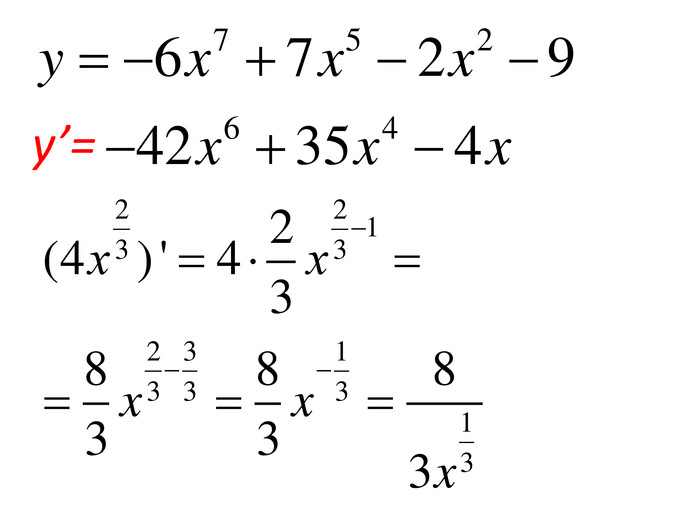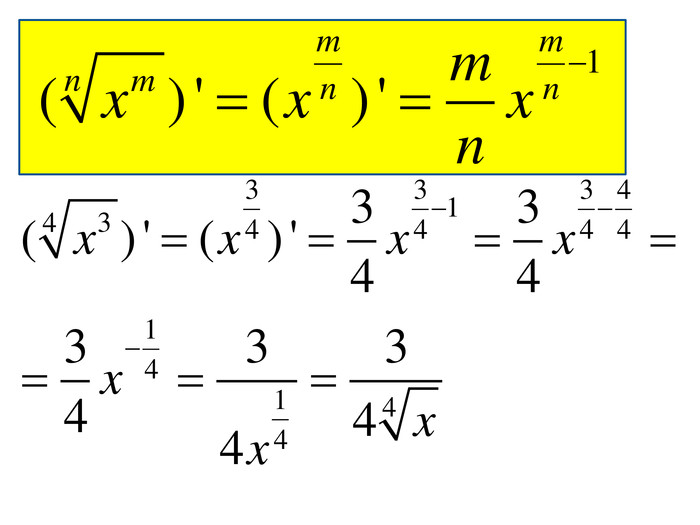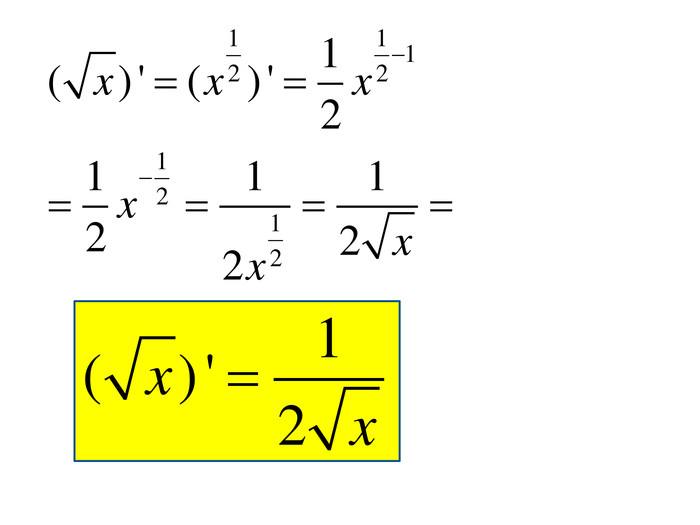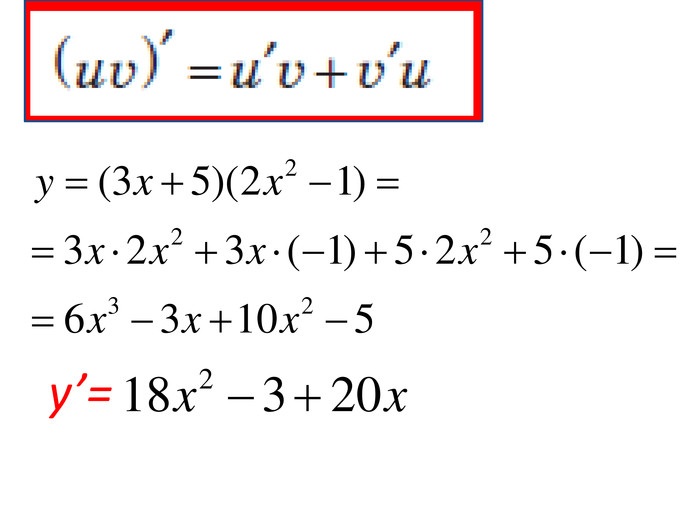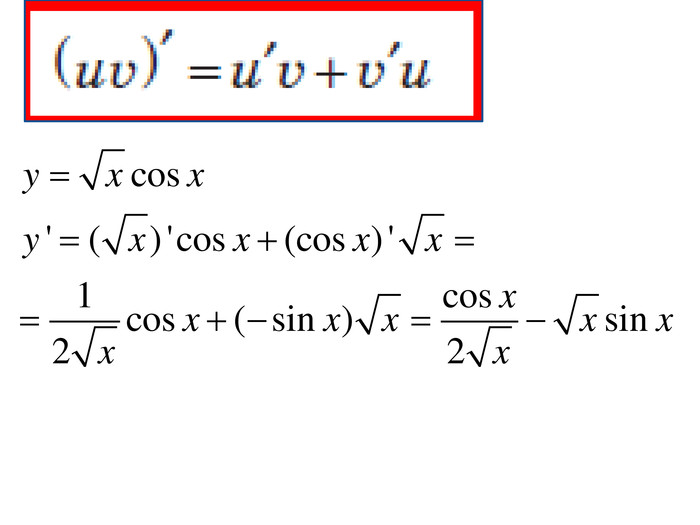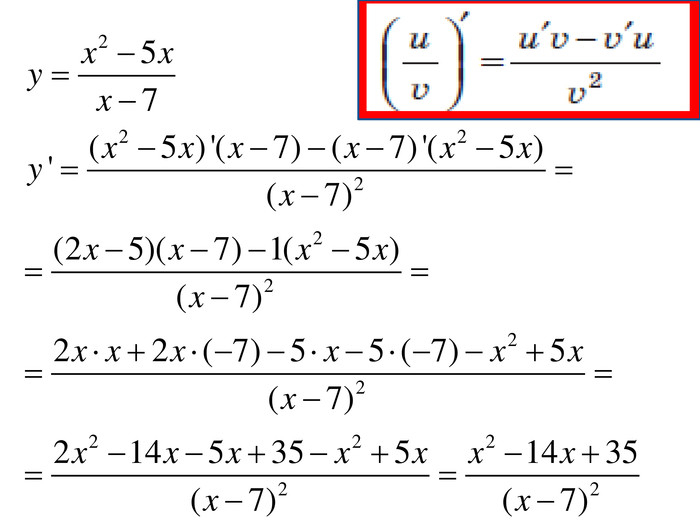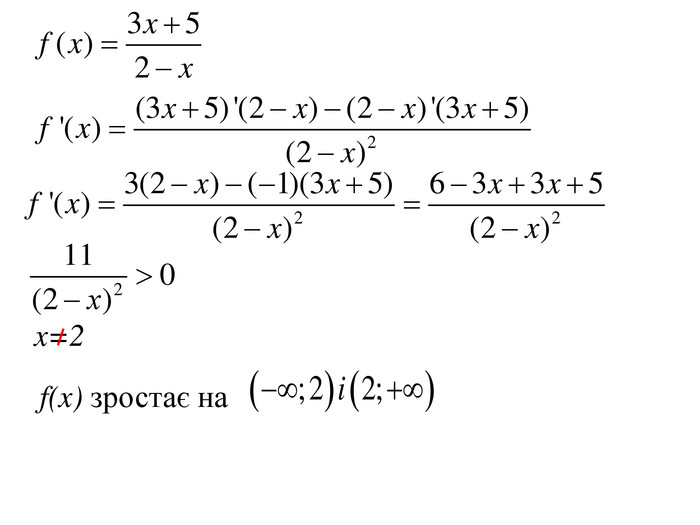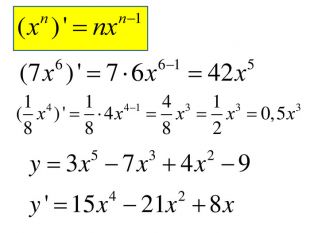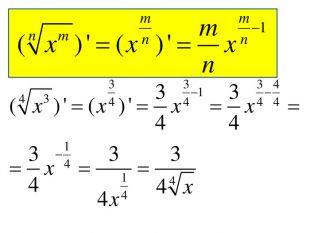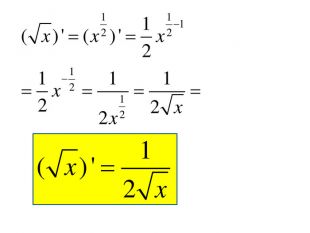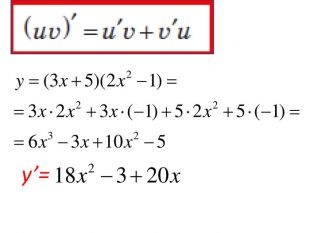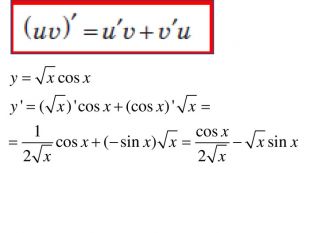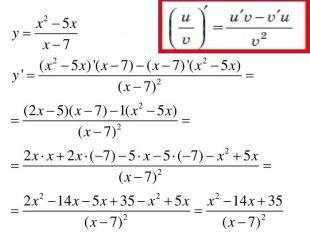Презентація за темою: "Похідна"
Про матеріал
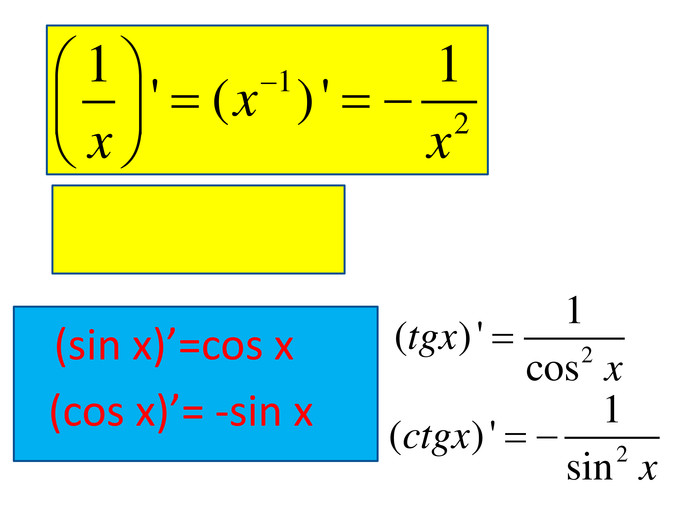
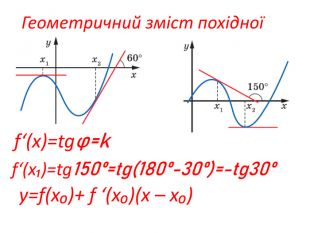
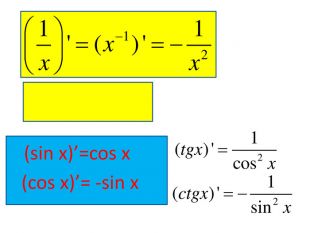
Розробка містить приклади обчислення похідних та приклади дослідження функції на монотонність Зміст архіву
- Åα«¿ºó«ñ¡á∩.pptx pptx
Перегляд файлу
Зміст слайдів
zip
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку