Презентація за темою "Роль та застосування індукції в математиці"
Про матеріал
Презентація за темою "Роль та застосування індукції в математиці"
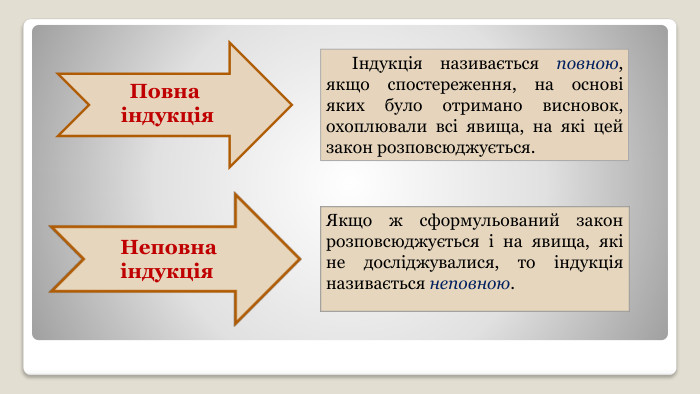
Роль індуктивних висновків в експериментальних науках дуже велика. Вони дають змогу довести ті положення, з яких потім шляхом дедукціі робляться подальші висновки. У математиці індукція часто дозволяє вгадати формулювання теорем, а в ряді випадків і намітити шляхи доведення.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку